Мый сійӧ e лыд? — различия между версиями
Наста (сёрнитанін | чӧжӧс) (→Сьӧм прӧчентъяс арталӧм) |
Наста (сёрнитанін | чӧжӧс) (→Содтӧд юӧр) |
||
| (не показаны 4 промежуточные версии этого же участника) | |||
| Строка 18: | Строка 18: | ||
[[Файл:Jakob Bernoulli.jpg|thumb|center|330px|]] | [[Файл:Jakob Bernoulli.jpg|thumb|center|330px|]] | ||
| − | ==Факториалъяс да e лыд== | + | ==Факториалъяс да ''e'' лыд== |
| − | Мед n — кутшӧмкӧ эма лыд; сылӧн факториалӧн шусьӧ 1∙2∙3∙4∙...∙(n − 1) | + | Мед ''n'' — кутшӧмкӧ эма лыд; сылӧн факториалӧн шусьӧ 1∙2∙3∙4∙...∙(''n'' − 1)∙''n'' лыд. Сійӧс пасйӧны кыдзи ''n''! (лыддьӧны: ''n'' факториал). Шуам, 1! = 1, 2! = 1∙2 = 2, 3! = 1∙2∙3 = 6, 4! = 1∙2∙3∙4 = 24, 5! = 1∙2∙3∙4∙5 = 120, да с.в. |
Ӧні вайӧй гижам со кутшӧм суммаяс: | Ӧні вайӧй гижам со кутшӧм суммаяс: | ||
| Строка 34: | Строка 34: | ||
... | ... | ||
| − | 1 + 1/1! +1/2! + 1/3! + 1/4! + ... + 1/n! | + | 1 + 1/1! +1/2! + 1/3! + 1/4! + ... + 1/''n''! |
... | ... | ||
| − | Вӧлӧмкӧ, n лыдсӧ помтӧг ыдждӧдӧмӧн бара воам e лыдӧ. (Кӧсъянныд кӧ, компьютер либӧ калькулятор отсӧгӧн арталӧй тайӧ суммаяссӧ да аддзанныд, кыдзи найӧ вочасӧн матыстчӧны 2,718281828459045... лыд дорӧ.) | + | Вӧлӧмкӧ, ''n'' лыдсӧ помтӧг ыдждӧдӧмӧн бара воам ''e'' лыдӧ. (Кӧсъянныд кӧ, компьютер либӧ калькулятор отсӧгӧн арталӧй тайӧ суммаяссӧ да аддзанныд, кыдзи найӧ вочасӧн матыстчӧны 2,718281828459045... лыд дорӧ.) |
==Петкӧдлан функция, чут координата да ӧд== | ==Петкӧдлан функция, чут координата да ӧд== | ||
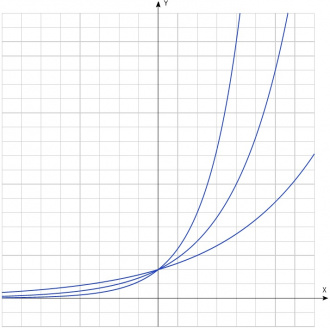
| − | Школаысь ми тӧдмалім петкӧдлан функция йылысь. Сетӧма кӧ кутшӧмкӧ плюса a лыд, быд x лыдлы сійӧ сетӧ f(x) = | + | Школаысь ми тӧдмалім петкӧдлан функция йылысь. Сетӧма кӧ кутшӧмкӧ плюса ''a'' лыд, быд ''x'' лыдлы сійӧ сетӧ ''f''(''x'') = ''a''<sup>''x''</sup> лыдсӧ; ''a'' лыдыс кӧ 1-ысь гырысьджык, петкӧдлан функцияыслӧн со кутшӧм график (серпас вылас куим график: ''a'' = 1,5; ''a'' = 2; ''a'' = 3 лыдъяслы): |
[[Файл:Exp function.jpg|thumb|center|330px|]] | [[Файл:Exp function.jpg|thumb|center|330px|]] | ||
| − | Вӧлӧмкӧ, a кӧ лоӧ e, тайӧ функцияыслӧн эм интереснӧй аслыспӧлӧслун. Мед чут мунӧ веськыд визьӧд да быд t кад здукӧ сылӧн координатаыс лоӧ | + | Вӧлӧмкӧ, ''a'' кӧ лоӧ ''e'', тайӧ функцияыслӧн эм интереснӧй аслыспӧлӧслун. Мед чут мунӧ веськыд визьӧд да быд ''t'' кад здукӧ сылӧн координатаыс лоӧ ''e''<sup>''t''</sup>. Вӧлӧмкӧ, быд ''t'' кад здукӧ и ӧдыс лоӧ ''e''<sup>''t''</sup>. Тайӧ аслыссикаслун понда ''e'' лыд математикъяслы да физикъяслы зэв ёна колана. |
==Пасйӧд== | ==Пасйӧд== | ||
==Содтӧд юӧр== | ==Содтӧд юӧр== | ||
| − | [ | + | [http://lovziem.blogspot.com/2020/11/e.html Велӧдӧм паськӧдан блогын] |
[[Category:Математика]] | [[Category:Математика]] | ||
Текущая версия на 19:59, 29 вӧльгым 2020
Содержание
Терминъяс
эма лыд — натуральное число петкӧдлан функция — показательная функция
Сьӧм прӧчентъяс арталӧм
Со ми пуктім банкӧ 1 сюрс шайт. Во помын кӧ банкыс содтӧ 100%, миянлы бӧр сетасны 2 сюрс шайт.
Мый артмас, банкыс кӧ вонас кыкысь прӧчентъяс содтӧ? Стӧчджыка кӧ, во джын мысти кӧ содӧ 50%, а сэсся нӧшта 50% содас (артмӧм суммаысь)? Бӧр сетасны 1,5∙1,5 = 1,52 = 2,25 сюрс шайт.
Мый нӧ артмас, банкыс кӧ вонас n‐ысь прӧчентъяс содтавны кутас? Во n‐ӧд юкӧн мысти артмас 1+1/n сюрс шайт. Сэсся, бара во n‐ӧд юкӧн мысти банкыс содтас 1+1/n шайтысь нӧшта n‐ӧд юкӧн. Артмас (1+1/n)∙(1+1/n) сюрс шайт. Сы бӧрын банкыс бара содтас n‐ӧд юкӧн, ӧні нин (1+1/n)∙(1+1/n) сюрс шайтысь. Артмас (1+1/n)∙(1+1/n)∙(1+1/n) сюрс шайт. Во помын миян лоас (1+1/n)n сюрс шайт.
Вӧлӧмкӧ, тшӧкыдджыка кӧ прӧчентъяс артавны кутам (гырысьджык n лыд кӧ босьтам), во помын унджык сьӧм воас. Но вывті ыджыд барыш оз ло: вӧлӧмкӧ, n лыдсӧ помтӧг содтӧмӧн воам e ≈ 2,718281828459045... сюрс шайтӧ.
Банк прӧчентъяс арталӧм йылысь гижӧд 1690-ӧд воын йӧзӧдӧма Яков Бернулли, швейцарияса математик.
Факториалъяс да e лыд
Мед n — кутшӧмкӧ эма лыд; сылӧн факториалӧн шусьӧ 1∙2∙3∙4∙...∙(n − 1)∙n лыд. Сійӧс пасйӧны кыдзи n! (лыддьӧны: n факториал). Шуам, 1! = 1, 2! = 1∙2 = 2, 3! = 1∙2∙3 = 6, 4! = 1∙2∙3∙4 = 24, 5! = 1∙2∙3∙4∙5 = 120, да с.в.
Ӧні вайӧй гижам со кутшӧм суммаяс:
1 + 1/1!;
1 + 1/1! +1/2!;
1 + 1/1! +1/2! + 1/3!;
1 + 1/1! +1/2! + 1/3! + 1/4!;
...
1 + 1/1! +1/2! + 1/3! + 1/4! + ... + 1/n!
...
Вӧлӧмкӧ, n лыдсӧ помтӧг ыдждӧдӧмӧн бара воам e лыдӧ. (Кӧсъянныд кӧ, компьютер либӧ калькулятор отсӧгӧн арталӧй тайӧ суммаяссӧ да аддзанныд, кыдзи найӧ вочасӧн матыстчӧны 2,718281828459045... лыд дорӧ.)
Петкӧдлан функция, чут координата да ӧд
Школаысь ми тӧдмалім петкӧдлан функция йылысь. Сетӧма кӧ кутшӧмкӧ плюса a лыд, быд x лыдлы сійӧ сетӧ f(x) = ax лыдсӧ; a лыдыс кӧ 1-ысь гырысьджык, петкӧдлан функцияыслӧн со кутшӧм график (серпас вылас куим график: a = 1,5; a = 2; a = 3 лыдъяслы):
Вӧлӧмкӧ, a кӧ лоӧ e, тайӧ функцияыслӧн эм интереснӧй аслыспӧлӧслун. Мед чут мунӧ веськыд визьӧд да быд t кад здукӧ сылӧн координатаыс лоӧ et. Вӧлӧмкӧ, быд t кад здукӧ и ӧдыс лоӧ et. Тайӧ аслыссикаслун понда e лыд математикъяслы да физикъяслы зэв ёна колана.