Рёло куимпельӧса — различия между версиями
Наста (сёрнитанін | чӧжӧс) (→Кыдзи нӧшта позьӧ вӧдитчыны Рёло куимпельӧсаӧн?) |
Наста (сёрнитанін | чӧжӧс) (→История йылысь кыв-мӧд) |
||
| Строка 134: | Строка 134: | ||
Кӧть куимпельӧсаыслы сетӧма 19-ӧд нэмся инженерлысь нимсӧ, сы йылысь тӧдӧмаӧсь ёна водзджык. Шуам, 18-ӧд нэмын Леонард Эйлер туялӧма ӧтпасьтаа мыгӧръяс, сійӧ пӧ и Рёло куимпельӧса йылысь гижлӧма. Куимпельӧсаыс паныдасьлӧ Леонардо да Винчилӧн гижӧдъясын; сы отсӧгӧн вӧлі лӧсьӧдӧма ставмувывса мусерпас: му веркӧсыс юклӧма кӧкъямыс пельӧ, быд юкӧн петкӧдлӧма тшӧтшкӧс вылын кыдзи Рёло куимпельӧса. | Кӧть куимпельӧсаыслы сетӧма 19-ӧд нэмся инженерлысь нимсӧ, сы йылысь тӧдӧмаӧсь ёна водзджык. Шуам, 18-ӧд нэмын Леонард Эйлер туялӧма ӧтпасьтаа мыгӧръяс, сійӧ пӧ и Рёло куимпельӧса йылысь гижлӧма. Куимпельӧсаыс паныдасьлӧ Леонардо да Винчилӧн гижӧдъясын; сы отсӧгӧн вӧлі лӧсьӧдӧма ставмувывса мусерпас: му веркӧсыс юклӧма кӧкъямыс пельӧ, быд юкӧн петкӧдлӧма тшӧтшкӧс вылын кыдзи Рёло куимпельӧса. | ||
| + | |||
| + | [[Файл:Da vinci muserpas.jpg|thumb|center|220px|]] | ||
Но и таысь на водзын йӧзыс тӧдлӧмаӧсь тайӧ мыгӧр йывсьыс: шуам, Брюгге карын Нотр-дам вичколӧн некымын ӧшиньлӧн формаыс — буретш Рёло куимпельӧса; вичкосӧ лэптӧмаӧсь 12−13-ӧд нэмӧ. | Но и таысь на водзын йӧзыс тӧдлӧмаӧсь тайӧ мыгӧр йывсьыс: шуам, Брюгге карын Нотр-дам вичколӧн некымын ӧшиньлӧн формаыс — буретш Рёло куимпельӧса; вичкосӧ лэптӧмаӧсь 12−13-ӧд нэмӧ. | ||
Версия 13:36, 21 ӧшым 2021
Содержание
Терминъяс
тшӧтшкӧс — плоскость кытшвизь — окружность кытш — круг куимпельӧса — треугольник вежтас — граница мылькъя мыгӧр — выпуклая фигура веськыд визь — прямая мыджан веськыд визь — опорная прямая инман веськыд визь — касательная прямая ӧтпасьтаа мыгӧр — фигура с постоянной шириной эрд — площадь вежтас — граница вундӧг — отрезок
Артмӧдӧм
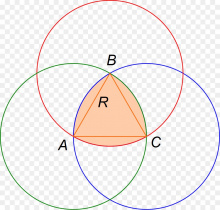
Тшӧтшкӧс вылын гижтам кутшӧмкӧ кытшвизь (мед сылӧн радиусыс лоӧ R). Босьтам сы вылын кутшӧмкӧ чут (пасъям сійӧс A шыпасӧн). Гижтам A шӧрчута да R радиуса кытшвизь. Артмӧдӧм кытшвизьясыслӧн эм кык ӧтувъя чут. Босьтам на пиысь ӧтиӧс да пасъям сійӧс B шыпасӧн, сэсся гижтам B шӧрчута да R радиуса кытшвизь.
Артмӧдӧм куим кытшъясыслӧн ӧтувъя юкӧныс шусьӧ Рёло (Reuleaux) куимпельӧсаӧн. Сылӧн вежтасыс тэчӧма куим кытшвизьлӧн мегыръясысь — AB, BC да AC‐ысь.
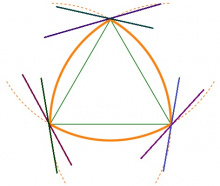
Мыджан веськыдъяс
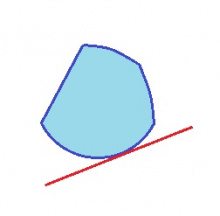
Тшӧтшкӧсвывса мылькъя мыгӧрлӧн эм со кутшӧм аслыспӧлӧслун: сылӧн вежтасвывса быд чут пыр позьӧ гижтыны веськыд визь сідзи, медым мыгӧрыс куйліс сыладорсянь ӧти тшӧтшкӧсджынйын. Татшӧм веськыд визьыс шусьӧ мыджан веськыд визьӧн.
Видлӧг. Мед мылькъя мыгӧрлӧн вежтас юкӧн лоӧ кытшвизь мегырӧн. Босьтам тайӧ мегыр вылас кутшӧмкӧ чут да сы пыр гижтам кытшвизяс инман веськыд визьсӧ. Сійӧ лоас мыджан веськыд визьӧн.
Рёло куимпельӧсалӧн вежтасвывса чут кӧ куйлӧ дзик ӧти кытшвизь мегыр вылын, сы пыр мунӧ сӧмын ӧти мыджан веськыд визь — инман веськыд. Чутыс кӧ куйлӧ кык кытшвизь вомӧнасянінын, сы пыр мунӧ помтӧм уна мыджан веськыд визь.
Ӧтпасьтаа мылькъя мыгӧръяс
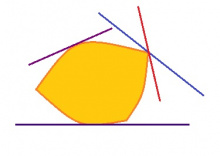
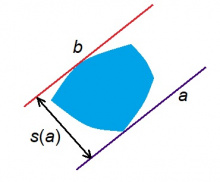
Мед тшӧтшкӧс вылын эм мылькъя мыгӧр. Гижтам кутшӧмкӧ мыджан веськыд визь (пасъям сійӧс a шыпасӧн) да пондам сійӧс вештыны параллель ногӧн мыгӧрсӧ кутысь тшӧтшкӧсджын пытшкас. Мед кутшӧмкӧ здукӧ вештӧм веськыдыс бара лоас мыджан визьӧн (пасъям сійӧс b шыпасӧн). Мыгӧрыс лоас топӧдӧма a да b костӧ. Мурталам a-сянь b‐ӧдз ылнасӧ да пасъям сійӧс s(a).
Мед s(a) лыд оз вежсьы, кутам кӧ вежлавны a‐сӧ (мыджан веськыд визьсӧ). Сэки мыгӧрыс шусьӧ ӧтпасьтааӧн; s = s(a) лыдсӧ шуӧны мыгӧрыслӧн пасьтаӧн.
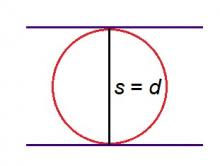
1-ӧд видлӧг. Кытш — ӧтпасьтаа мыгӧр; пасьтаыс ӧтыджда сылӧн диаметркӧд.
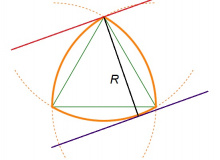
2-ӧд видлӧг. Рёло куимпельӧса — ӧтпасьтаа мыгӧр. Сійӧ кӧ тэчӧма R радиуса кытшвизьяслӧн мегыръясысь, пасьтаыс лоӧ R: куимпельӧсаыс кӧ топӧдӧма кык параллель веськыд визь костас, ӧтиыс инмӧ кытшвизь мегырӧ, мӧдыс мунӧ тайӧ кытшвизьыслӧн шӧрчут пыр.
Вӧлӧмкӧ, s‐пасьтаа мылькъя мыгӧръяс пӧвстын Рёло куимпельӧса медічӧт эрда. Тайӧ теоремасӧ йӧзӧдӧмаӧсь Анри Лебег 1914-ӧд воын да Вильгельм Бляшке 1915-ӧд воын.
Мылькъя мыгӧрлӧн йывъяс да пельӧсъяс
Мед M — мылькъя мыгӧр, a — сылӧн вежтасвывса чут; a шусьӧ йылӧн, сы пыр кӧ позьӧ гижтыны кык торъялана мыджан веськыд визь.
Казьтыштам: Рёло куимпельӧсалӧн вежтасыс тэчӧма куим кытшвизь мегырысь. Сідзкӧ, Рёло куимпельӧсалӧн эм куим йыв (кытшвизьясыслӧн вомӧнасян чутъяс).
Мед a чут — M мыгӧрлӧн йыв. Гижтам a пыр став мыджан веськыд визь (серпас вылын визьяслысь куйланінсӧ пасйӧма турунвиж рӧмӧн). Тшӧтшкӧсыс юксьӧ нёль пельӧ, быд юкӧныс — a йыла пельӧс. На пиысь ӧтиыс кутӧ M-сӧ. Сійӧ шусьӧ M мыгӧрлӧн пельӧсӧн.
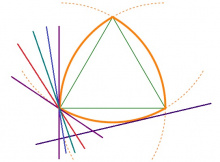
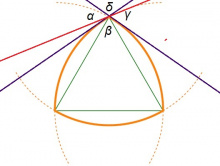
Рёло куимпельӧсалӧн пельӧсъясыс. Рёло куимпельӧсалӧн йыв лоӧ кык кытшвизьлӧн вомӧнасян чутӧн. Гижтам сы пыр кытшвизьясас инман веськыд визьяс. Найӧ юкӧны тшӧтшкӧссӧ нёль юкӧнӧ: α, β, γ, δ.
Серпас вылас петкӧдлӧма: йыв пыр мунысь мыджан веськыд визь юксьӧ кык пельӧ; ӧти сылӧн джынйыс куйлӧ α пельӧсын, мӧдыс — γ пельӧсын. Рёло куимпельӧса куйлӧ β-ын.
Арталам β-лысь ыдждасӧ. Серпас вылас тайӧ — ∠dae.
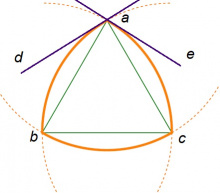
abc куимпельӧса ӧткодь доръяса (быд сылӧн дор — кытшвизьлӧн радиус). Сідзкӧ, ∠bac = 60°. ad да ae — инман веськыдъяс, та вӧсна ∠cad = ∠bae = 90°, ∠dab = ∠eac = 90° − 60° = 30°. Миян артмис:
∠dae = ∠cad + ∠eac = 90° + 30° = 120°.
Та вӧсна Рёло куимпельӧсалӧн быд пельӧсыс 120° ыджда.
Вӧлӧмкӧ, мылькъя мыгӧр кӧ ӧтпасьтаа, сылӧн пельӧсъясыс оз вермыны лоны 120°-ысь ичӧтджык. Сідзкӧ, Рёло куимпельӧса — медічӧт пельӧсъяса ӧтпасьтаа мыгӧр.
Рёло куимпельӧса да квадрат
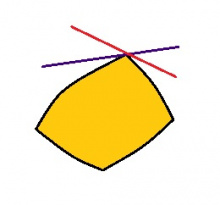
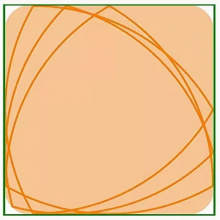
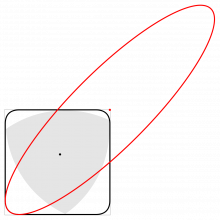
Тӧрӧдам квадрат пытшкӧ Рёло куимпельӧса (квадратыслӧн быд дор лоас мыджан веськыд визьса вундӧгӧн) да пондам сійӧс быгльӧдны. Кутшӧм мыгӧр вевттяс Рёло куимпельӧса тыр бергӧдлӧм вӧчӧм бӧрын?
Дзонь квадрат артмыны оз вермы: квадратлӧн пельӧсыс 90° ыджда, а Рёло куимпельӧсалӧн — 120° ыджда.
Вӧлӧмкӧ, артмас "шыльӧдӧм" квадрат; сылӧн вежтасыс тэчӧма нёль вундӧгысь да нёль эллипслӧн мегырысь.
Дзонь квадратысь вошӧ сӧмын неыджыд юкӧн: эрд серти кӧ, 2%‐ысь этшаджык.
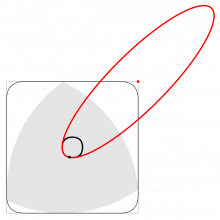
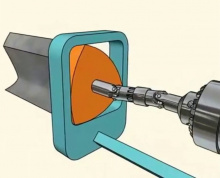
Та вӧсна позьӧ вӧчны пӧшти квадрат формаа розь вундалысь дрель. Сійӧс лӧсьӧдӧма 1914-ӧд воын англияса инженер Гарри Джеймс Уаттс. Сверлӧыс — Рёло куимпельӧсалӧн юкӧн (сійӧс петкӧдлӧма серпас вылас руд рӧмӧн).
Нӧшта колӧ шуны: Рёло куимпельӧса быгыльтчигӧн сылӧн шӧрчутыс ӧти местаын оз сулав. Сійӧ гижтӧ нёль эллипслӧн мегыръясысь тэчӧм визьсӧ.
Та вӧсна колӧ, медым сверлӧыс вермис вешъявны.
Кыдзи нӧшта позьӧ вӧдитчыны Рёло куимпельӧсаӧн?
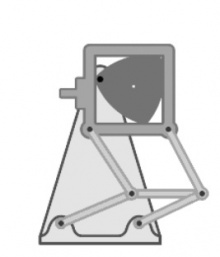
Ачыс Франц Рёло (1829−1905), немеч инженер, туялӧма ӧти сикаса мунӧм мӧд сикаса мунӧмӧ вуджӧдан механизмъяс. Кутшӧмсюрӧ механизмъяслӧн юкӧннас вӧлі Рёло куимпельӧса. Вӧлӧмкӧ, водзынджык, 1830-ӧд воясӧ, Рёло куимпельӧсаӧн вӧдитчӧмаӧсь нин руӧн уджалан машинаяс вӧчигӧн.
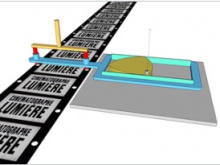
Ми висьтавлім, кыдзи Рёло куимпельӧса быгыльтчӧ квадрат пытшкын (тыр бергӧдлӧм бӧрын сійӧ вевттьӧ квадратсӧ пӧшти дзоньнас — эрд серти кӧ, 98%-ысь унджык). Тайӧ принцип серти уджалӧ Уаттлӧн дрель (сы йылысь гижлім нин) да кинопроекторын плёнка йӧткан механизм. Рёло куимпельӧса эм Люмьер вокъяслӧн машинаын
да "Луч−2" проекторын.
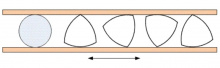
Вайӧй ӧні тӧд вылӧ уськӧдам: Рёло куимпельӧса — ӧтпасьтаа мыгӧр. Та вӧсна, пуктам кӧ пӧв Рёло куимпельӧса подула цилиндръяс вылӧ, сійӧ кутас быгыльтчыны сідзи жӧ бура, кыдзи и гӧгрӧс цилиндръяс вылын.
(А бур кӧлеса Рёло куимпельӧсаысь оз нин артмы: быгыльтчигас сылӧн шӧрчутыс вешъялӧ ӧтарӧ-мӧдарӧ.)
История йылысь кыв-мӧд
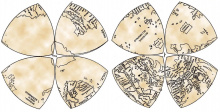
Кӧть куимпельӧсаыслы сетӧма 19-ӧд нэмся инженерлысь нимсӧ, сы йылысь тӧдӧмаӧсь ёна водзджык. Шуам, 18-ӧд нэмын Леонард Эйлер туялӧма ӧтпасьтаа мыгӧръяс, сійӧ пӧ и Рёло куимпельӧса йылысь гижлӧма. Куимпельӧсаыс паныдасьлӧ Леонардо да Винчилӧн гижӧдъясын; сы отсӧгӧн вӧлі лӧсьӧдӧма ставмувывса мусерпас: му веркӧсыс юклӧма кӧкъямыс пельӧ, быд юкӧн петкӧдлӧма тшӧтшкӧс вылын кыдзи Рёло куимпельӧса.
Но и таысь на водзын йӧзыс тӧдлӧмаӧсь тайӧ мыгӧр йывсьыс: шуам, Брюгге карын Нотр-дам вичколӧн некымын ӧшиньлӧн формаыс — буретш Рёло куимпельӧса; вичкосӧ лэптӧмаӧсь 12−13-ӧд нэмӧ.