Эрд да йӧрыш мурталӧм — различия между версиями
Наста (сёрнитанін | чӧжӧс) (→Ньютон–Лейбниц формула йылысь) |
Наста (сёрнитанін | чӧжӧс) (→Графикувса юкӧнлӧн эрд йылысь) |
||
| (не показано 39 промежуточных версий этого же участника) | |||
| Строка 21: | Строка 21: | ||
веськыдсэрӧг — прямоугольник | веськыдсэрӧг — прямоугольник | ||
ӧтмоза мунӧм — равномерное движение | ӧтмоза мунӧм — равномерное движение | ||
| + | тшӧтшкӧс — плоскость | ||
| + | вундӧг — отрезок | ||
| + | урчитӧм — определение | ||
| + | пельӧм — дробь | ||
| + | кыв вожалӧм — противоречие | ||
==Важ Египетын да Вавилонын эрд да йӧрыш мурталӧм== | ==Важ Египетын да Вавилонын эрд да йӧрыш мурталӧм== | ||
| Строка 79: | Строка 84: | ||
XVII–XVIII нэмӧ Ньютон да Лейбниц лӧсьӧдӧмаӧсь дифференциал да интеграл артасьӧм. Йӧрышъяс да эрдъяс сы отсӧгӧн корсьны абу нин вывті сьӧкыд. Дженьыдика висьталам тайӧ артасьӧм йывсьыс. | XVII–XVIII нэмӧ Ньютон да Лейбниц лӧсьӧдӧмаӧсь дифференциал да интеграл артасьӧм. Йӧрышъяс да эрдъяс сы отсӧгӧн корсьны абу нин вывті сьӧкыд. Дженьыдика висьталам тайӧ артасьӧм йывсьыс. | ||
| − | [[Файл:Newton leibnitz.jpg|thumb|center| | + | [[Файл:Newton leibnitz.jpg|thumb|center|330px|]] |
===Здукся ӧд.=== | ===Здукся ӧд.=== | ||
| Строка 99: | Строка 104: | ||
Мед ''f''(''t'') ≥ 0 — функция, ''t''<sub>0</sub> ≤ ''t'' ≤ ''t''<sub>1</sub>. Видлалам сылӧн график да ''t'' чӧрс костын куйлысь став чутсӧ. Шуам тайӧ мыгӧрсӧ графикувса юкӧнӧн. Кыдзи артавны сылысь эрдсӧ? | Мед ''f''(''t'') ≥ 0 — функция, ''t''<sub>0</sub> ≤ ''t'' ≤ ''t''<sub>1</sub>. Видлалам сылӧн график да ''t'' чӧрс костын куйлысь став чутсӧ. Шуам тайӧ мыгӧрсӧ графикувса юкӧнӧн. Кыдзи артавны сылысь эрдсӧ? | ||
| + | |||
| + | [[Файл:Grafikuvsa.jpg|thumb|center|220px|]] | ||
Медводз видлалам ''f''(''t'') = ''v'' функциясӧ. Сэки графикувса юкӧн лоӧ веськыдсэрӧгӧн: ӧти дорыс лоӧ ''t''<sub>1</sub> − ''t''<sub>0</sub>, мӧд дорыс лоӧ ''v''. Сідзкӧ, сылӧн эрдыс лоӧ ''v''(''t''<sub>1</sub> − ''t''<sub>0</sub>). | Медводз видлалам ''f''(''t'') = ''v'' функциясӧ. Сэки графикувса юкӧн лоӧ веськыдсэрӧгӧн: ӧти дорыс лоӧ ''t''<sub>1</sub> − ''t''<sub>0</sub>, мӧд дорыс лоӧ ''v''. Сідзкӧ, сылӧн эрдыс лоӧ ''v''(''t''<sub>1</sub> − ''t''<sub>0</sub>). | ||
| + | |||
| + | [[Файл:V const.jpg|thumb|center|220px|]] | ||
Вайӧй ӧні ӧтмоза мунӧм видлалам. Мед чут вешйӧ ''v'' ӧднас. Сэки сылӧн координатаыс ''t''<sub>0</sub>‐сянь ''t''<sub>1</sub>‐ӧдз кадколастӧ со кыдзи вежсяс: ''x''(''t''<sub>1</sub>) − ''x''(''t''<sub>0</sub>) = ''v''(''t''<sub>1</sub> − ''t''<sub>0</sub>). | Вайӧй ӧні ӧтмоза мунӧм видлалам. Мед чут вешйӧ ''v'' ӧднас. Сэки сылӧн координатаыс ''t''<sub>0</sub>‐сянь ''t''<sub>1</sub>‐ӧдз кадколастӧ со кыдзи вежсяс: ''x''(''t''<sub>1</sub>) − ''x''(''t''<sub>0</sub>) = ''v''(''t''<sub>1</sub> − ''t''<sub>0</sub>). | ||
| + | |||
| + | [[Файл:V c coord.jpg|thumb|center|220px|]] | ||
Сідзкӧ, вежласьтӧм ӧдлӧн графикувса юкӧнлӧн эрд да координата вежласьӧм лоӧ ӧти сійӧ жӧ лыдӧн. | Сідзкӧ, вежласьтӧм ӧдлӧн графикувса юкӧнлӧн эрд да координата вежласьӧм лоӧ ӧти сійӧ жӧ лыдӧн. | ||
Мед ӧні ''f''(''t'') функция "тэчӧма" некымын константаысь: ''t''<sub>0</sub>‐сянь ''t''<sub>1</sub>‐ӧдз сійӧ лоӧ ''v''<sub>1</sub>, ''t''<sub>1</sub>‐сянь ''t''<sub>2</sub>‐ӧдз сійӧ лоӧ ''v''<sub>2</sub>, ''t''<sub>2</sub>‐сянь ''t''<sub>3</sub>‐ӧдз сійӧ лоӧ ''v''<sub>3</sub>, да сідз водзӧ. Сэки сылӧн графикувса юкӧн тэчӧма некымын веськыдсэрӧгысь; сідзкӧ, медым артавны сылысь эрдсӧ, колӧ содтыны ''v''<sub>1</sub>(''t''<sub>1</sub> − ''t''<sub>0</sub>), ''v''<sub>2</sub>(''t''<sub>2</sub> − ''t''<sub>1</sub>), ''v''<sub>3</sub>(''t''<sub>3</sub>− ''t''<sub>2</sub>) да с.в. | Мед ӧні ''f''(''t'') функция "тэчӧма" некымын константаысь: ''t''<sub>0</sub>‐сянь ''t''<sub>1</sub>‐ӧдз сійӧ лоӧ ''v''<sub>1</sub>, ''t''<sub>1</sub>‐сянь ''t''<sub>2</sub>‐ӧдз сійӧ лоӧ ''v''<sub>2</sub>, ''t''<sub>2</sub>‐сянь ''t''<sub>3</sub>‐ӧдз сійӧ лоӧ ''v''<sub>3</sub>, да сідз водзӧ. Сэки сылӧн графикувса юкӧн тэчӧма некымын веськыдсэрӧгысь; сідзкӧ, медым артавны сылысь эрдсӧ, колӧ содтыны ''v''<sub>1</sub>(''t''<sub>1</sub> − ''t''<sub>0</sub>), ''v''<sub>2</sub>(''t''<sub>2</sub> − ''t''<sub>1</sub>), ''v''<sub>3</sub>(''t''<sub>3</sub>− ''t''<sub>2</sub>) да с.в. | ||
| + | |||
| + | [[Файл:Piece const.jpg|thumb|center|220px|]] | ||
Чут кӧ мунӧ ''f''(''t'') здукся ӧдӧн, сылӧн координатаыс со кыдзи вежласяс: ''t''<sub>0</sub>‐сянь ''t''<sub>1</sub>‐ӧдз кадколастӧ сійӧ содас ''v''<sub>1</sub>(''t''<sub>1</sub> − ''t''<sub>0</sub>)-ӧн, ''t''<sub>1</sub>‐сянь ''t''<sub>2</sub>‐ӧдз кадколастӧ сійӧ содас ''v''<sub>2</sub>(''t''<sub>2</sub> − ''t''<sub>1</sub>)-ӧн, да с.в. Медым тӧдмавны, кыдзи бӧръяпомыс вежсяс координатаыс, колӧ тайӧ став лыдсӧ содтыны. | Чут кӧ мунӧ ''f''(''t'') здукся ӧдӧн, сылӧн координатаыс со кыдзи вежласяс: ''t''<sub>0</sub>‐сянь ''t''<sub>1</sub>‐ӧдз кадколастӧ сійӧ содас ''v''<sub>1</sub>(''t''<sub>1</sub> − ''t''<sub>0</sub>)-ӧн, ''t''<sub>1</sub>‐сянь ''t''<sub>2</sub>‐ӧдз кадколастӧ сійӧ содас ''v''<sub>2</sub>(''t''<sub>2</sub> − ''t''<sub>1</sub>)-ӧн, да с.в. Медым тӧдмавны, кыдзи бӧръяпомыс вежсяс координатаыс, колӧ тайӧ став лыдсӧ содтыны. | ||
| + | |||
| + | [[Файл:Piece coord.jpg|thumb|center|220px|]] | ||
Бара миян артмис: ӧдлӧн графикувса юкӧнлӧн эрд да координата вежласьӧм лоӧ ӧти сійӧ жӧ лыд. | Бара миян артмис: ӧдлӧн графикувса юкӧнлӧн эрд да координата вежласьӧм лоӧ ӧти сійӧ жӧ лыд. | ||
| Строка 117: | Строка 132: | ||
Мед, шуам, ''f''(''t'') = 3''t''<sup>2</sup>. Ми тӧдам нин: ''x''(''t'') кӧ лоӧ ''t''<sup>3</sup>, ''f''(''t'') и лоас здукся ӧдӧн. Сідзкӧ, босьтны кӧ ''t''<sub>0</sub> ≤ ''t'' ≤ ''t''<sub>1</sub>, графикувса юкӧнлысь эрдсӧ арталам формула серти: ''S'' = ''t''<sub>1</sub><sup>3</sup> − ''t''<sub>0</sub><sup>3</sup>. | Мед, шуам, ''f''(''t'') = 3''t''<sup>2</sup>. Ми тӧдам нин: ''x''(''t'') кӧ лоӧ ''t''<sup>3</sup>, ''f''(''t'') и лоас здукся ӧдӧн. Сідзкӧ, босьтны кӧ ''t''<sub>0</sub> ≤ ''t'' ≤ ''t''<sub>1</sub>, графикувса юкӧнлысь эрдсӧ арталам формула серти: ''S'' = ''t''<sub>1</sub><sup>3</sup> − ''t''<sub>0</sub><sup>3</sup>. | ||
| + | |||
| + | [[Файл:Parabolauvsa.jpg|thumb|center|220px|]] | ||
А тӧдам кӧ парабола графикувса юкӧнлысь эрд, кужам, сідзкӧ, парабола сегментлысь эрдсӧ артавны. Архимедлы та вылӧ ковмис вӧчны ыджыд удж да зэв ыджыд кужӧм петкӧдлыны. | А тӧдам кӧ парабола графикувса юкӧнлысь эрд, кужам, сідзкӧ, парабола сегментлысь эрдсӧ артавны. Архимедлы та вылӧ ковмис вӧчны ыджыд удж да зэв ыджыд кужӧм петкӧдлыны. | ||
| + | |||
| + | ==Графикувса юкӧнлӧн эрд йылысь== | ||
| + | |||
| + | XVIII‐ӧд нэмын зэв бура кужлӧмаӧсь Ньютон–Лейбниц формулаӧн вӧдитчыны, воанлыдъяс артавны и. Уна мича формула вӧлі артмӧдӧма сійӧ кадас. Сӧмын сэки эз на вӧв стӧча урчитӧма мый сэтшӧмыс воанлыд. Кутшӧмсюрӧ сьӧкыдторъясысь сэки видзчысьӧмаӧсь на. Шуам, ӧти математик шулӧма: помтӧм сумма арталӧмын кӧ воанлыдыс абу — тайӧ пӧ антуссянь суммаыс (мистицизмсьыс сэки абу жӧ на мынтӧдчӧмаӧсь). | ||
| + | |||
| + | XIX‐ӧд нэмӧ прансуз математик Огюстен Луи Коши пондас студентъясӧс велӧдны дай мӧвпавны кутас: кыдзи налы стӧчджыка гӧгӧрвоӧдны, эм-абу воанлыд да мыйла. Бӧръяпомыс сійӧ лӧсьӧдӧма воанлыдъяс йылысь теория. | ||
| + | |||
| + | [[Файл:Cauchy1.jpg|thumb|center|170px|]] | ||
| + | |||
| + | Водзын ми висьталім функция графикувса эрд йылысь. 1854-ӧд воын Георг Фридрих Бернхард Риман, немеч математик, сетӧма стӧч урчитӧм — кыдзи тайӧ эрдсӧ муртавны. Сёрӧнджык, 1879-ӧд воын, прансуз математик Жан Гастон Дарбу сӧвмӧдӧма Риманлысь теориясӧ. | ||
| + | |||
| + | [[Файл:Riemann darboux.png|thumb|center|330px|]] | ||
| + | |||
| + | Шӧр мӧвпыс со кутшӧм. Сетӧма ''f''(''t'') функция, ''a'' ≤ ''t'' ≤ ''b''. | ||
| + | |||
| + | [[Файл:Riem sum11.jpg|thumb|center|330px|]] | ||
| + | |||
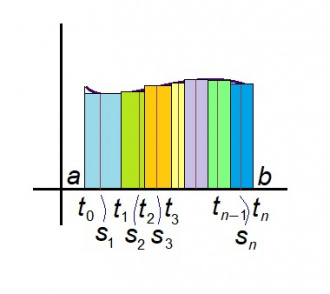
| + | Юклам вундӧгсӧ ''a'' = ''t''<sub>0</sub> < ''t''<sub>1</sub> < ''t''<sub>2</sub> < ... < ''t''<sub>''n''−1</sub> < ''t''<sub>''n''</sub> = ''b'' чутъясӧн да бӧръям кутшӧмкӧ ''s''<sub>1</sub>, ''s''<sub>2</sub>, ..., ''s''<sub>''n''</sub> чутъяс сідзи, медым ''t''<sub>0</sub> ≤ ''s''<sub>1</sub> ≤ ''t''<sub>1</sub>, ''t''<sub>1</sub> ≤ ''s''<sub>2</sub> ≤ ''t''<sub>2</sub> да с.в. | ||
| + | |||
| + | [[Файл:Riem sum2.jpg|thumb|center|330px|]] | ||
| + | |||
| + | Сы бӧрын со кутшӧм сумма лӧсьӧдам: | ||
| + | |||
| + | (''t''<sub>1</sub> − ''t''<sub>0</sub>)''f''(''s''<sub>1</sub>) + (''t''<sub>2</sub> − ''t''<sub>1</sub>)''f''(''s''<sub>2</sub>) + ... + (''t''<sub>''n''</sub> − ''t''<sub>''n''−1</sub>)''f''(''s''<sub>''n''</sub>). | ||
| + | |||
| + | Тайӧ лоас эрдсӧ ылӧсас арталӧм. Сэсся кутам посньӧдны юклан вундӧгъяссӧ, медым налӧн кузьтаясыс вӧліны 0 дорӧ матынджык и матынджык. Артмӧдӧм суммаясыслӧн кӧ эм воанлыд — сійӧ и лоас графикувса эрдӧн. | ||
| + | |||
| + | XIX‐ӧд нэмын Ньютон–Лейбниц теория вӧлі подулалӧма. | ||
| + | |||
| + | ==Жордан ногӧн эрд да йӧрыш мурталӧм== | ||
| + | |||
| + | Водзын ми висьталім: XIX‐ӧд нэм шӧрын Риман сетӧма стӧч урчитӧм — мый тайӧ функция графикувса юкӧнлӧн эрд. Сёрӧнджык, XIX‐ӧд нэм помын нин, вӧлі сетӧма стӧч урчитӧм — мый тайӧ тшӧтшкӧс мыгӧрлӧн эрд либӧ куим муртӧса телӧлӧн йӧрыш. Урчитӧмсӧ вӧзйӧмаӧсь италияса математик Джузеппе Пеано 1887-ӧд воын да прансуз математик Мари Энмон Камиль Жордан 1892-ӧд воын. | ||
| + | |||
| + | [[Файл:Jordan Peano.jpg|thumb|center|270px|]] | ||
| + | |||
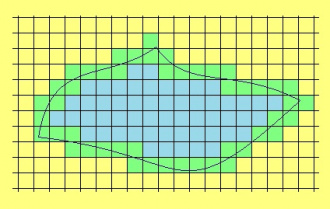
| + | Медшӧр идеяыс со кутшӧм. Школаын миянӧс велӧдісны, кыдзи ылӧсас артавны мыгӧрлысь эрдсӧ. Юклам тшӧтшкӧссӧ посни квадратъяс вылӧ. Сэсся босьтам мыгӧр пытшкас куйлысь став квадратсӧ да арталам ӧтласа эрдсӧ. | ||
| + | |||
| + | [[Файл:Erd murtalem.jpg|thumb|center|330px|]] | ||
| + | |||
| + | Позьӧ и мӧд ногӧн вӧчны: босьтны став квадратсӧ, кодлӧн эм кӧть ӧти ӧтувъя чут мыгӧрыскӧд, да налысь ӧтласа эрдсӧ артавны. Вӧлӧмкӧ, мыгӧрлӧн дорыс кӧ абу вывті дзуг, тайӧ кык лыдыс лоасны ӧта-мӧдлы матыссаӧсь. | ||
| + | |||
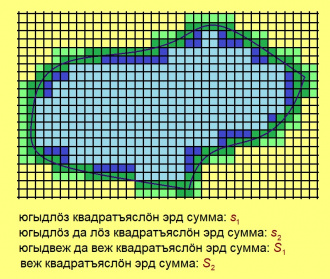
| + | Сідзкӧ, со кыдзи Жордан ногӧн мыгӧрлысь эрдсӧ урчитны. Юклам тшӧтшкӧссӧ квадратъяс вылӧ. Босьтам мыгӧр пытшкас куйлысь став квадратсӧ да арталам налысь эрд суммасӧ (пасъям сійӧс ''s''<sub>1</sub>). Сэсся босьтам став квадрат, кодлӧн эм кӧть ӧти ӧтувъя чут сетӧм мыгӧрыскӧд, да налысь эрд суммасӧ арталам (пасъям сійӧс ''S''<sub>1</sub>). | ||
| + | |||
| + | [[Файл:S1s2.jpg|thumb|center|330px|]] | ||
| + | |||
| + | Сэсся посньӧдам квадратъяссӧ налысь доръяссӧ кык пельӧ юклӧмӧн, да сэтшӧм жӧ ногӧн арталам квадратъяслысь эрд суммаяссӧ. Артмасны лыдъяс: ''s''<sub>2</sub> да ''S''<sub>2</sub>. Казялам: ''s''<sub>2</sub> ≥ ''s''<sub>1</sub> (квадрат кӧ куйлӧ мыгӧр пытшкас, сылӧн став юкӧн тшӧтш куйлӧ мыгӧр пытшкас), ''S''<sub>2</sub> ≤ ''S''<sub>1</sub> (квадрат юкӧнлӧн кӧ эм мыгӧрыскӧд кӧть ӧти ӧтувъя чут, дзонь квадратлӧн сійӧ тшӧтш эм). | ||
| + | |||
| + | Посньыдджык квадратъяслысь доръяссӧ бара кык пельӧ юклам да артмӧдам выль суммаяссӧ: ''s''<sub>3</sub> да ''S''<sub>3</sub>, да сідз водзӧ. | ||
| + | |||
| + | Гижам сьӧрсьӧн-бӧрсьӧн лыдъяссӧ: ''s''<sub>1</sub> ≤ ''s''<sub>2</sub> ≤ ''s''<sub>3</sub> ≤ ''s''<sub>4</sub> ≤ ... Вӧлӧмкӧ, налӧн эм воанлыд (пасъям сійӧс ''s'' шыпасӧн). Сэсся гижам лыдъяссӧ: ''S''<sub>1</sub> ≥ ''S''<sub>2</sub> ≥ ''S''<sub>3</sub> ≥ ''S''<sub>4</sub> ≥ ... Налӧн, вӧлӧм, тшӧтш эм воанлыд (пасъям сійӧс ''S'' шыпасӧн). Жордан серти, мыгӧрлӧн эм эрд, ''s'' да ''S'' лыдъясыс кӧ ӧткодьӧсь. | ||
| + | |||
| + | Тадзи жӧ урчитӧны куим муртӧса телӧлысь йӧрышсӧ (квадратъяс пыдди кубъяс босьтӧмӧн). | ||
| + | |||
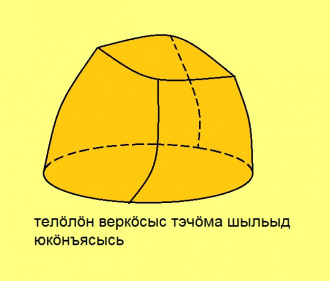
| + | Вӧлӧмкӧ, мыгӧрлӧн дорыс (телӧлӧн веркӧсыс) кӧ тэчӧма некымын шыльыд юкӧнъясысь, сылӧн эрдыс (йӧрышыс) эм. Шуам, кытшлӧн, кытш секторлӧн, кытш сегментлӧн, эллипс пытшкӧслӧн, парабола сегментлӧн эм эрд, а шарлӧн, цилиндрлӧн, конуслӧн, тшӧтшӧдӧм конуслӧн эм йӧрыш. | ||
| + | |||
| + | [[Файл:Piecewise smooth.jpg|thumb|center|330px|]] | ||
| + | |||
| + | Ми аддзам: функциялӧн графикувса юкӧнлысь эрдсӧ позьӧ кык ногӧн артавны — Риманлӧн урчитӧм серти да Жорданлӧн урчитӧм серти. Вӧлӧмкӧ, кыкнан методыс сетас ӧти сійӧ жӧ лыд. | ||
| + | |||
| + | ==Лебег ногӧн эрд да йӧрыш мурталӧм== | ||
| + | |||
| + | Сідзкӧ, XIX‐ӧд нэм пом кежлӧ математикъяс урчитӧмаӧсь, мый сэтшӧмыс эрд да йӧрыш. Эрд да йӧрыш арталан формулаяссӧ сідзжӧ подулалӧмаӧсь. Но регыд мысти математикъяслы Жорданлӧн да Риманлӧн теорияыс эз нин ло тырмымӧн: найӧ пондӧмаӧсь туявны веськыд визьлысь, тшӧтшкӧслысь да ылдӧслысь зэв дзуг юкӧнъяс. (Колӧ шуны, пӧрысьджык математикъяс пӧвстысь кодсюрӧ татшӧм "лёкторъяс" видлалӧмлы паныд сувтлӧма, весиг гижлӧма, зывӧкпырысь пӧ та вылӧ видзӧда. Но XX‐ӧд нэмын лои гӧгӧрвоана: "консерваторъяс" абу правӧсь.) | ||
| + | |||
| + | Вайӧй со кутшӧм мыгӧр видлалам. Босьтам (0, 0), (0, 1), (1, 0) да (1, 1) йывъяса квадрат (пасъям сійӧс ''K'' шыпасӧн) да бӧръям сы пытшкӧсса рациональ лыда координатаяса став чутсӧ (рациональ лыд — тайӧ ''m''/''n'' пельӧм, кӧні ''m'' да ''n'' — дзонь лыдъяс). Пасъям тайӧ чут чукӧрсӧ ''M'' шыпасӧн. Петкӧдлам: ''M''‐лысь эрдсӧ оз позь артавны Жордан ногӧн. | ||
| + | |||
| + | Юклам ''K'' квадратсӧ ӧткодь посни квадратъяс вылӧ да видлам ылӧсас артавны ''M''‐лысь эрдсӧ, кыдзи водзын висьтавлім. | ||
| + | |||
| + | 1) Босьтам став квадратсӧ, кӧні эм кӧть ӧти ӧтувъя чут ''M''‐кӧд, да арталам налысь эрд суммасӧ. Но быд квадратлӧн шӧрчутыс куйлӧ ''M''‐ын: сылӧн кыкнан координатаыс рациональ. Сідзкӧ, колӧ артавны эрд суммасӧ став квадратыслысь. Тайӧ лоас 1 (''K''-лӧн эрд). Посньӧдам кӧ квадратъяссӧ, бара артмас 1. Та вӧсна ''M''‐лӧн эрд лоӧ 1 (позьӧ кӧ сійӧс Жордан ногӧн артавны). | ||
| + | |||
| + | [[Файл:K m.jpg|thumb|center|270px|]] | ||
| + | |||
| + | 2) Ӧні босьтам ''M'' пытшкас куйлысь став квадратсӧ да арталам налысь эрд суммасӧ. Но быд квадрат пытшкын эм иррациональ абсциссаа чут. Сідзкӧ, ни ӧти квадрат ''M''-ӧ тӧрӧдны оз позь, та вӧсна суммаыс лоас 0. Посньӧдам кӧ квадратъяссӧ, бара лоас 0. Та вӧсна ''M''‐лӧн эрдыс лоӧ 0. | ||
| + | |||
| + | Со мый артмис: ӧтарсянь кӧ, ''M''‐лӧн эрдыс лоӧ 1, мӧдарсянь кӧ, сійӧ жӧ лоӧ 0. Тайӧ кыв вожалӧм. | ||
| + | |||
| + | 1901–1904-ӧд воясӧ Анри Лебег, прансуз математик, лӧсьӧдӧма выль теория. Сійӧ петкӧдлӧма, кыдзи мӧд ног позьӧ артавны эрдъяс да йӧрышъяс, а сідзжӧ функциялӧн графикувса юкӧнлысь эрдсӧ. | ||
| + | |||
| + | [[Файл:Lebesgue 2 1.jpeg|thumb|center|270px|]] | ||
| + | |||
| + | Лебег теория йылысь тані огӧ нин кутӧй висьтавны, пасъям сӧмын некымын результат. | ||
| + | |||
| + | 1) Позьӧ кӧ артавны мыгӧрлысь эрдсӧ (йӧрышсӧ) Жордан ногӧн — позьӧ артавны и Лебег ногӧн; артмас ӧткодь лыд. | ||
| + | |||
| + | 2) Кутшӧмкӧ мыгӧръяслысь эрдъяссӧ оз позь артавны Жордан ногӧн, но позьӧ артавны Лебег ногӧн. Водзын ми висьтавлім ''M'' мыгӧр йылысь (квадрат пытшкӧсса рациональ лыда координатаяса став чут). Вӧлӧмкӧ, Лебег ногӧн арталӧм эрдыс лоас 0. | ||
| + | |||
| + | 3) Позьӧ кӧ артавны функциялӧн графикувса юкӧнлысь эрдсӧ Риман ногӧн, сійӧс жӧ позьӧ артавны и Лебег ногӧн; артмас ӧткодь лыд. | ||
| + | |||
| + | 4) Кутшӧмсюрӧ функцияяслӧн графикувса юкӧнлысь эрдсӧ оз позь артавны Риман ногӧн, но позьӧ артавны Лебег ногӧн. | ||
| + | |||
| + | Сідзкӧ, Лебеглӧн арталан ногыс бурджык Жорданлӧн да Риманлӧн арталан ногысь: унджыктор позьӧ муртавны. | ||
| + | |||
| + | Нӧшта со мый пасъям. | ||
| + | |||
| + | 5) Мед ''A'' мыгӧр торйӧдӧма ''A''<sub>1</sub>, ''A''<sub>2</sub>, ''A''<sub>3</sub>, ..., ''A''<sub>''n''</sub>, ... мыгӧръяс вылӧ (помтӧм уна юкӧнъяс вылӧ, найӧс позьӧ нумеруйтны да сьӧрсьӧн-бӧрсьӧн гижны). Мед быд тайӧ юкӧнлысь эрдсӧ (йӧрышсӧ) позьӧ артавны Лебег ногӧн. Вӧлӧмкӧ, ''A''-лысь эрдсӧ (йӧрышсӧ) тшӧтш позьӧ артавны Лебег ногӧн; сійӧ лоас ''A''<sub>1</sub>, ''A''<sub>2</sub>, ''A''<sub>3</sub>, ''A''<sub>4</sub>, ..., ''A<sub>n</sub>'', ... мыгӧръяслӧн эрд суммаӧн. | ||
| + | |||
| + | [[Файл:Lebesgue lectures.jpg|thumb|center|270px|]] | ||
| + | |||
| + | Лебег ассьыс теориясӧ лӧсьӧдӧма да лача кутӧма: гашкӧ, быд мыгӧрлысь эрдсӧ (йӧрышсӧ) позяс муртавны? Вӧлӧмкӧ, оз. Та вылӧ видзӧдтӧг, Лебег теория XX‐ӧд нэмся математикъяслы зэв коланаторйӧн лои. | ||
==Пасйӧд== | ==Пасйӧд== | ||
| Строка 128: | Строка 243: | ||
[http://lovziem.blogspot.com/2021/04/3.html Велӧдӧм паськӧдан блогын – 3.] | [http://lovziem.blogspot.com/2021/04/3.html Велӧдӧм паськӧдан блогын – 3.] | ||
| + | |||
| + | [http://lovziem.blogspot.com/2021/04/5.html Велӧдӧм паськӧдан блогын – 4.] | ||
| + | |||
| + | [http://lovziem.blogspot.com/2021/05/5.html Велӧдӧм паськӧдан блогын – 5.] | ||
| + | |||
| + | [http://lovziem.blogspot.com/2021/05/6.html Велӧдӧм паськӧдан блогын – 6.] | ||
[[Category:Математика]] | [[Category:Математика]] | ||
Текущая версия на 20:18, 28 кӧч 2022
Содержание
Терминъяс
тшӧтшкӧс мыгӧр — плоская фигура эрд — площадь куим муртӧса — трёхмерный йӧрыш — объём тшӧтшӧдӧм куимпельӧса — усечённый треугольник (трапеция) судта — высота лыдмӧдны — умножить висьталӧм — утверждение куимпельӧса — треугольник подув — основание судта — высота ӧтгырся — равновеликий тӧрӧдӧм мыгӧр — вписанная фигура воанлыд — предел вомӧнасянін — пересечение артасьӧм — исчисление шӧр ӧд — средняя скорость здукся ӧд — мгновенная скорость чӧрс — ось веськыдсэрӧг — прямоугольник ӧтмоза мунӧм — равномерное движение тшӧтшкӧс — плоскость вундӧг — отрезок урчитӧм — определение пельӧм — дробь кыв вожалӧм — противоречие
Важ Египетын да Вавилонын эрд да йӧрыш мурталӧм
Тшӧтшкӧс мыгӧръяслысь эрдъяссӧ да куим муртӧса телӧяслысь йӧрышъяссӧ артавлӧмаӧсь Важ Египетын на. Шуам, Ахмес папирусын (сійӧ жӧ Райнд папирусӧн шусьӧ) со кутшӧм гижӧд эм:
"Кутшӧм эрд тшӧтшӧдӧм куимпельӧсалӧн, сылӧн судтаыс кӧ 20 хет, подулыс кӧ 6 хет, а вылыс подулыс кӧ 4 хет кузьта? Ӧтлаӧдӧй улыс подувсӧ вылыскӧдыс. Артмӧданныд 10. Юклӧй 10 лыдсӧ 2 пельӧ. А сэсся 5 босьтӧй 20 пӧв..."
Тшӧтшӧдӧм куимпельӧса — тайӧ трапеция. Гижӧд сертиыс позьӧ аддзыны: эрдсӧ стӧча артавлӧмаӧсь (подувъяслысь сумма джынсӧ да судтасӧ лыдмӧдӧмаӧсь).
Важ египтяна кужлӧмаӧсь тшӧтшӧдӧм пирамидалысь йӧрышсӧ артавны и. Математика йылысь Мӧскуаса папирусын со кутшӧм задача эм:
"Шуасны тэныд: со тшӧтшӧдӧм пирамида, судтаыс 6, улыс дорыс 4, вылыс дорыс 2. Артав 4-лысь квадрат. Тайӧ лоас 16. Кыкмындаав 4 лыдсӧ. Тайӧ лоас 8. Артав 2-лысь квадрат. Тайӧ лоас 4. Ӧтлаӧд артмӧдӧм 16, 8 да 4-сӧ. Тайӧ лоас 28. Артав 6 лыдлысь коймӧд юкӧн. Тайӧ лоас 2. Кыкмындаав 28 лыдсӧ. Тайӧ лоас 56. Видзӧд: тайӧ 56. Тэ колана лыдсӧ артмӧдін."
Тшӧтшӧдӧм пирамидаыслӧн подувъясыс кӧ квадратъяс, 56 лоас сылӧн йӧрышӧн.
Кытшлысь эрдсӧ египтяна ылӧсалӧмӧн артавлӧмаӧсь: сетӧма кӧ d диаметрыс, эрд пыдди найӧ гижлӧмаӧсь (8d/9)2.
Важ вавилоняна сідзжӧ эрдъяс да йӧрышъяс муртавлӧмаӧсь. Кытш эрд корсигӧн найӧ абу египтяна моз арталӧмаӧсь, мӧд ылӧсалан формулаясӧн вӧдитчӧмаӧсь. Кужлӧмаӧсь и кытш сегментлысь эрдсӧ, тшӧтшӧдӧм конуслысь йӧрышсӧ артавны (дерт, бара жӧ ылӧсалӧмӧн).
Важ Египетын да Вавилонын сӧмын арталанног сетавлӧмаӧсь, подулавтӧг.
Важ Элладаын эрд да йӧрыш мурталӧм
Важ Элладаын тӧдмалӧмаӧсь египетса да вавилонса математика йылысь да некымын нэм чӧж асьныс ёна сӧвмӧдӧмаӧсь наукасӧ. Буретш сэки математикъяс пондӧмаӧсь подулавны ассьыныс висьталӧмъяссӧ (теоремаяссӧ).
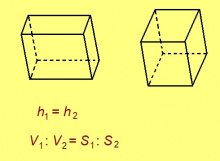
Евклидлӧн "Элементъяс" гижӧдыс сиӧма геометрия да арифметика теориялы. Медводдза небӧгын эмӧсь куимпельӧсалӧн да параллелограммлӧн эрдъяс йылысь со кутшӧм теоремаяс: кык куимпельӧсалӧн (параллелограммлӧн) кӧ подувъясыс ӧтыдждаӧсь да судтаясыс ӧтыдждаӧсь, налӧн эрдъясыс ӧтыдждаӧсь жӧ. 11-ӧд небӧгын эмӧсь параллелепипед да призма йӧрышъяс йылысь теоремаяс (шуам: кык параллелепипедлӧн кӧ подувъясыс ӧтгырсяӧсь да судтаясыс ӧтыдждаӧсь, налӧн йӧрышъясыс ӧтыдждаӧсь жӧ; ӧткодь судтаа параллелограммъяслӧн йӧрышъясыс да налӧн подувъяслӧн эрдъясыс артмӧдӧны пропорция, да с.в.).
Кытш эрд да шар йӧрыш йылысь теоремаяс эмӧсь жӧ "Элементъяс"-ын. Кыдзи нӧ найӧс подулалӧмаӧсь?
Вӧлӧмкӧ, важ элладасаяс аслыспӧлӧс метод лӧсьӧдӧмаӧсь (сідз шусяна "помӧдз видзӧм ног"; рочӧн кӧ, "метод исчерпывания", англичан кывйӧн кӧ, "method of exhaustion"). Медводз сійӧс, буракӧ, вӧзйӧма Антифон. Книдса Евдокс бура сӧвмӧдӧма тайӧ методсӧ. Медшӧр идеяыс со кутшӧм. Медым артавны мыгӧрлысь эрдсӧ либӧ йӧрышсӧ, сыӧ сьӧрсьӧн-бӧрсьӧн тӧрӧдӧны мукӧд мыгӧръяс, кодъяслысь эрдъяссӧ (йӧрышъяссӧ) тӧдӧны нин. Быд тӧрӧдӧм мыгӧр пытшкас воддза мыгӧрыс куйлӧ дзоньнас.
Эрдъяссӧ (йӧрышъяссӧ) арталӧны да гижӧны сьӧрсьӧн-бӧрсьӧн: S1, S2, ..., Sn, ... Сэсся зільӧны гӧгӧрвоны, кутшӧм лыдӧ воасны тайӧ ыдждаясыс, n лыдсӧ помтӧг содтӧмӧн. Важ Элладаын воанлыдъяс йылысь теория абу на вӧлӧма лӧсьӧдӧма да, тайӧ методнас вӧдитчыны зэв сьӧкыд вӧлі. Медводз корсяна эрд (йӧрыш) йылысь гипотеза вӧзйӧмаӧсь, сэсся петкӧдлӧмаӧсь, мыйла кутшӧмкӧ мӧд ыджда оз вермы лоны воанлыдӧн.
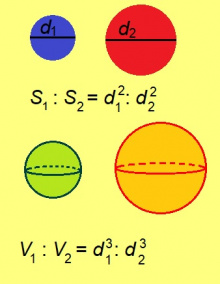
"Элементъяс"-са 12-ӧд небӧгын эм кытшлӧн эрд йылысь теорема (эрдыс лоӧ пропорцияын диаметрыслӧн кузьта квадраткӧд), шарлӧн йӧрыш йылысь теорема (йӧрышыс лоӧ пропорцияын диаметрыслӧн кузьта кубкӧд), тетраэдр йӧрыш йылысь теорема (кык тетраэдрлӧн кӧ судтаясыс ӧткодьӧсь, йӧрышъясыс лоӧны подувъяслӧн эрдъяскӧд пропорцияын), конус да цилиндр йӧрыш йылысь некымын теорема. Буракӧ, тайӧ юкӧдыс вӧлі гижӧма Евдокс результатъяс вылӧ подулалӧмӧн.
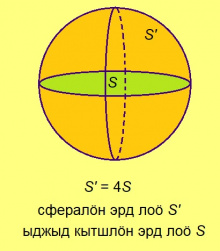
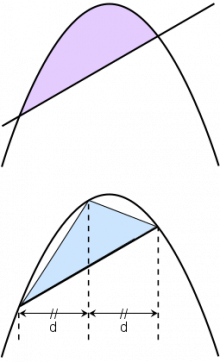
Архимед водзӧ сӧвмӧдӧма Евдокслысь методсӧ да кужӧма артавны сфералысь эрдсӧ (сфералӧн эрд ыджыд кытшлӧн эрдысь нёль пӧв ыджыдджык; ыджыд кытш — тайӧ шарлӧн да сылӧн шӧрчут пыр мунысь тшӧтшкӧслӧн вомӧнасянін).
Сійӧ жӧ арталӧма парабола сегментлысь эрдсӧ.
Ньютон–Лейбниц формула йылысь
XVII–XVIII нэмӧ Ньютон да Лейбниц лӧсьӧдӧмаӧсь дифференциал да интеграл артасьӧм. Йӧрышъяс да эрдъяс сы отсӧгӧн корсьны абу нин вывті сьӧкыд. Дженьыдика висьталам тайӧ артасьӧм йывсьыс.
Здукся ӧд.
Мед кутшӧмкӧ чут ветлӧ веськыд визьӧд, t кад здукӧ сылӧн координатаыс лоӧ x(t). Сетӧма кӧ t‐сянь t + s‐ӧдз кадколаст, позьӧ артавны чутлысь шӧр ӧдсӧ (s лыд вермӧ лоны плюсаӧн да минусаӧн): vшӧр = [x(t + s) − x(t)]/s.
Видлалам x(t) = t3. Сэки t‐сянь t + s‐ӧдз кадколастса шӧр ӧд лоас
[(t + s)3 − t3]/s = (t3 + 3t2s + 3ts2 + s3 − t3)/s = 3t2 + 3ts + s2.
Вайӧй кутам ичӧтмӧдны s лыдсӧ 0-ӧдз. Тадзи 3t2 + 3ts + s2 пондас матыстчыны 3t2 лыдлань да бӧръяпомыс сыӧ и воас. Артмӧм воанлыд шусьӧ t здукся ӧдӧн.
Координата кӧ вежсьӧ кутшӧмкӧ мӧд формула серти, здукся ӧдсӧ позьӧ тадзи жӧ урчитны: гижны шӧр ӧдсӧ, сэсся s лыдсӧ 0-ӧдз ичӧтмӧдны; шӧр ӧдъясыслӧн кӧ эм воанлыд, сійӧ и шусьӧ здукся ӧдӧн.
Нӧшта ӧти видлӧг казьтыштам: x(t) = et (e лыд йылысь висьтавлім тані). Вӧлӧмкӧ, t здукся ӧд сідзи жӧ лоас et.
Здукся ӧд да графикувса юкӧнлӧн эрд костын йитӧд.
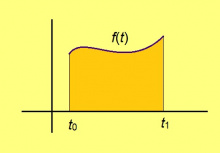
Мед f(t) ≥ 0 — функция, t0 ≤ t ≤ t1. Видлалам сылӧн график да t чӧрс костын куйлысь став чутсӧ. Шуам тайӧ мыгӧрсӧ графикувса юкӧнӧн. Кыдзи артавны сылысь эрдсӧ?
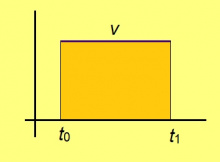
Медводз видлалам f(t) = v функциясӧ. Сэки графикувса юкӧн лоӧ веськыдсэрӧгӧн: ӧти дорыс лоӧ t1 − t0, мӧд дорыс лоӧ v. Сідзкӧ, сылӧн эрдыс лоӧ v(t1 − t0).
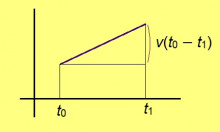
Вайӧй ӧні ӧтмоза мунӧм видлалам. Мед чут вешйӧ v ӧднас. Сэки сылӧн координатаыс t0‐сянь t1‐ӧдз кадколастӧ со кыдзи вежсяс: x(t1) − x(t0) = v(t1 − t0).
Сідзкӧ, вежласьтӧм ӧдлӧн графикувса юкӧнлӧн эрд да координата вежласьӧм лоӧ ӧти сійӧ жӧ лыдӧн.
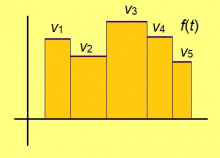
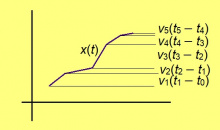
Мед ӧні f(t) функция "тэчӧма" некымын константаысь: t0‐сянь t1‐ӧдз сійӧ лоӧ v1, t1‐сянь t2‐ӧдз сійӧ лоӧ v2, t2‐сянь t3‐ӧдз сійӧ лоӧ v3, да сідз водзӧ. Сэки сылӧн графикувса юкӧн тэчӧма некымын веськыдсэрӧгысь; сідзкӧ, медым артавны сылысь эрдсӧ, колӧ содтыны v1(t1 − t0), v2(t2 − t1), v3(t3− t2) да с.в.
Чут кӧ мунӧ f(t) здукся ӧдӧн, сылӧн координатаыс со кыдзи вежласяс: t0‐сянь t1‐ӧдз кадколастӧ сійӧ содас v1(t1 − t0)-ӧн, t1‐сянь t2‐ӧдз кадколастӧ сійӧ содас v2(t2 − t1)-ӧн, да с.в. Медым тӧдмавны, кыдзи бӧръяпомыс вежсяс координатаыс, колӧ тайӧ став лыдсӧ содтыны.
Бара миян артмис: ӧдлӧн графикувса юкӧнлӧн эрд да координата вежласьӧм лоӧ ӧти сійӧ жӧ лыд.
Мед ӧні чутлӧн t кад здукся координата лоӧ x(t), а здукся ӧд лоӧ v(t). Вӧлӧмкӧ, и сэки ӧдлӧн графикувса юкӧнлӧн эрд да координата вежласьӧм лоӧ ӧти сійӧ жӧ лыд. (Тайӧ теорема шусьӧ Ньютон–Лейбниц формулаӧн.)
Сідзкӧ, сетӧма кӧ миянлы f(t) функция да тӧдам кӧ ми x(t) функциясӧ, кодлӧн f(t) лоӧ здукся ӧдӧн, вермам кокньыда артавны графикувса юкӧнлысь эрдсӧ.
Мед, шуам, f(t) = 3t2. Ми тӧдам нин: x(t) кӧ лоӧ t3, f(t) и лоас здукся ӧдӧн. Сідзкӧ, босьтны кӧ t0 ≤ t ≤ t1, графикувса юкӧнлысь эрдсӧ арталам формула серти: S = t13 − t03.
А тӧдам кӧ парабола графикувса юкӧнлысь эрд, кужам, сідзкӧ, парабола сегментлысь эрдсӧ артавны. Архимедлы та вылӧ ковмис вӧчны ыджыд удж да зэв ыджыд кужӧм петкӧдлыны.
Графикувса юкӧнлӧн эрд йылысь
XVIII‐ӧд нэмын зэв бура кужлӧмаӧсь Ньютон–Лейбниц формулаӧн вӧдитчыны, воанлыдъяс артавны и. Уна мича формула вӧлі артмӧдӧма сійӧ кадас. Сӧмын сэки эз на вӧв стӧча урчитӧма мый сэтшӧмыс воанлыд. Кутшӧмсюрӧ сьӧкыдторъясысь сэки видзчысьӧмаӧсь на. Шуам, ӧти математик шулӧма: помтӧм сумма арталӧмын кӧ воанлыдыс абу — тайӧ пӧ антуссянь суммаыс (мистицизмсьыс сэки абу жӧ на мынтӧдчӧмаӧсь).
XIX‐ӧд нэмӧ прансуз математик Огюстен Луи Коши пондас студентъясӧс велӧдны дай мӧвпавны кутас: кыдзи налы стӧчджыка гӧгӧрвоӧдны, эм-абу воанлыд да мыйла. Бӧръяпомыс сійӧ лӧсьӧдӧма воанлыдъяс йылысь теория.
Водзын ми висьталім функция графикувса эрд йылысь. 1854-ӧд воын Георг Фридрих Бернхард Риман, немеч математик, сетӧма стӧч урчитӧм — кыдзи тайӧ эрдсӧ муртавны. Сёрӧнджык, 1879-ӧд воын, прансуз математик Жан Гастон Дарбу сӧвмӧдӧма Риманлысь теориясӧ.
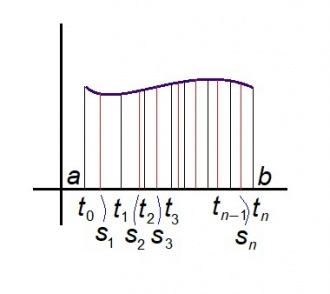
Шӧр мӧвпыс со кутшӧм. Сетӧма f(t) функция, a ≤ t ≤ b.
Юклам вундӧгсӧ a = t0 < t1 < t2 < ... < tn−1 < tn = b чутъясӧн да бӧръям кутшӧмкӧ s1, s2, ..., sn чутъяс сідзи, медым t0 ≤ s1 ≤ t1, t1 ≤ s2 ≤ t2 да с.в.
Сы бӧрын со кутшӧм сумма лӧсьӧдам:
(t1 − t0)f(s1) + (t2 − t1)f(s2) + ... + (tn − tn−1)f(sn).
Тайӧ лоас эрдсӧ ылӧсас арталӧм. Сэсся кутам посньӧдны юклан вундӧгъяссӧ, медым налӧн кузьтаясыс вӧліны 0 дорӧ матынджык и матынджык. Артмӧдӧм суммаясыслӧн кӧ эм воанлыд — сійӧ и лоас графикувса эрдӧн.
XIX‐ӧд нэмын Ньютон–Лейбниц теория вӧлі подулалӧма.
Жордан ногӧн эрд да йӧрыш мурталӧм
Водзын ми висьталім: XIX‐ӧд нэм шӧрын Риман сетӧма стӧч урчитӧм — мый тайӧ функция графикувса юкӧнлӧн эрд. Сёрӧнджык, XIX‐ӧд нэм помын нин, вӧлі сетӧма стӧч урчитӧм — мый тайӧ тшӧтшкӧс мыгӧрлӧн эрд либӧ куим муртӧса телӧлӧн йӧрыш. Урчитӧмсӧ вӧзйӧмаӧсь италияса математик Джузеппе Пеано 1887-ӧд воын да прансуз математик Мари Энмон Камиль Жордан 1892-ӧд воын.
Медшӧр идеяыс со кутшӧм. Школаын миянӧс велӧдісны, кыдзи ылӧсас артавны мыгӧрлысь эрдсӧ. Юклам тшӧтшкӧссӧ посни квадратъяс вылӧ. Сэсся босьтам мыгӧр пытшкас куйлысь став квадратсӧ да арталам ӧтласа эрдсӧ.
Позьӧ и мӧд ногӧн вӧчны: босьтны став квадратсӧ, кодлӧн эм кӧть ӧти ӧтувъя чут мыгӧрыскӧд, да налысь ӧтласа эрдсӧ артавны. Вӧлӧмкӧ, мыгӧрлӧн дорыс кӧ абу вывті дзуг, тайӧ кык лыдыс лоасны ӧта-мӧдлы матыссаӧсь.
Сідзкӧ, со кыдзи Жордан ногӧн мыгӧрлысь эрдсӧ урчитны. Юклам тшӧтшкӧссӧ квадратъяс вылӧ. Босьтам мыгӧр пытшкас куйлысь став квадратсӧ да арталам налысь эрд суммасӧ (пасъям сійӧс s1). Сэсся босьтам став квадрат, кодлӧн эм кӧть ӧти ӧтувъя чут сетӧм мыгӧрыскӧд, да налысь эрд суммасӧ арталам (пасъям сійӧс S1).
Сэсся посньӧдам квадратъяссӧ налысь доръяссӧ кык пельӧ юклӧмӧн, да сэтшӧм жӧ ногӧн арталам квадратъяслысь эрд суммаяссӧ. Артмасны лыдъяс: s2 да S2. Казялам: s2 ≥ s1 (квадрат кӧ куйлӧ мыгӧр пытшкас, сылӧн став юкӧн тшӧтш куйлӧ мыгӧр пытшкас), S2 ≤ S1 (квадрат юкӧнлӧн кӧ эм мыгӧрыскӧд кӧть ӧти ӧтувъя чут, дзонь квадратлӧн сійӧ тшӧтш эм).
Посньыдджык квадратъяслысь доръяссӧ бара кык пельӧ юклам да артмӧдам выль суммаяссӧ: s3 да S3, да сідз водзӧ.
Гижам сьӧрсьӧн-бӧрсьӧн лыдъяссӧ: s1 ≤ s2 ≤ s3 ≤ s4 ≤ ... Вӧлӧмкӧ, налӧн эм воанлыд (пасъям сійӧс s шыпасӧн). Сэсся гижам лыдъяссӧ: S1 ≥ S2 ≥ S3 ≥ S4 ≥ ... Налӧн, вӧлӧм, тшӧтш эм воанлыд (пасъям сійӧс S шыпасӧн). Жордан серти, мыгӧрлӧн эм эрд, s да S лыдъясыс кӧ ӧткодьӧсь.
Тадзи жӧ урчитӧны куим муртӧса телӧлысь йӧрышсӧ (квадратъяс пыдди кубъяс босьтӧмӧн).
Вӧлӧмкӧ, мыгӧрлӧн дорыс (телӧлӧн веркӧсыс) кӧ тэчӧма некымын шыльыд юкӧнъясысь, сылӧн эрдыс (йӧрышыс) эм. Шуам, кытшлӧн, кытш секторлӧн, кытш сегментлӧн, эллипс пытшкӧслӧн, парабола сегментлӧн эм эрд, а шарлӧн, цилиндрлӧн, конуслӧн, тшӧтшӧдӧм конуслӧн эм йӧрыш.
Ми аддзам: функциялӧн графикувса юкӧнлысь эрдсӧ позьӧ кык ногӧн артавны — Риманлӧн урчитӧм серти да Жорданлӧн урчитӧм серти. Вӧлӧмкӧ, кыкнан методыс сетас ӧти сійӧ жӧ лыд.
Лебег ногӧн эрд да йӧрыш мурталӧм
Сідзкӧ, XIX‐ӧд нэм пом кежлӧ математикъяс урчитӧмаӧсь, мый сэтшӧмыс эрд да йӧрыш. Эрд да йӧрыш арталан формулаяссӧ сідзжӧ подулалӧмаӧсь. Но регыд мысти математикъяслы Жорданлӧн да Риманлӧн теорияыс эз нин ло тырмымӧн: найӧ пондӧмаӧсь туявны веськыд визьлысь, тшӧтшкӧслысь да ылдӧслысь зэв дзуг юкӧнъяс. (Колӧ шуны, пӧрысьджык математикъяс пӧвстысь кодсюрӧ татшӧм "лёкторъяс" видлалӧмлы паныд сувтлӧма, весиг гижлӧма, зывӧкпырысь пӧ та вылӧ видзӧда. Но XX‐ӧд нэмын лои гӧгӧрвоана: "консерваторъяс" абу правӧсь.)
Вайӧй со кутшӧм мыгӧр видлалам. Босьтам (0, 0), (0, 1), (1, 0) да (1, 1) йывъяса квадрат (пасъям сійӧс K шыпасӧн) да бӧръям сы пытшкӧсса рациональ лыда координатаяса став чутсӧ (рациональ лыд — тайӧ m/n пельӧм, кӧні m да n — дзонь лыдъяс). Пасъям тайӧ чут чукӧрсӧ M шыпасӧн. Петкӧдлам: M‐лысь эрдсӧ оз позь артавны Жордан ногӧн.
Юклам K квадратсӧ ӧткодь посни квадратъяс вылӧ да видлам ылӧсас артавны M‐лысь эрдсӧ, кыдзи водзын висьтавлім.
1) Босьтам став квадратсӧ, кӧні эм кӧть ӧти ӧтувъя чут M‐кӧд, да арталам налысь эрд суммасӧ. Но быд квадратлӧн шӧрчутыс куйлӧ M‐ын: сылӧн кыкнан координатаыс рациональ. Сідзкӧ, колӧ артавны эрд суммасӧ став квадратыслысь. Тайӧ лоас 1 (K-лӧн эрд). Посньӧдам кӧ квадратъяссӧ, бара артмас 1. Та вӧсна M‐лӧн эрд лоӧ 1 (позьӧ кӧ сійӧс Жордан ногӧн артавны).
2) Ӧні босьтам M пытшкас куйлысь став квадратсӧ да арталам налысь эрд суммасӧ. Но быд квадрат пытшкын эм иррациональ абсциссаа чут. Сідзкӧ, ни ӧти квадрат M-ӧ тӧрӧдны оз позь, та вӧсна суммаыс лоас 0. Посньӧдам кӧ квадратъяссӧ, бара лоас 0. Та вӧсна M‐лӧн эрдыс лоӧ 0.
Со мый артмис: ӧтарсянь кӧ, M‐лӧн эрдыс лоӧ 1, мӧдарсянь кӧ, сійӧ жӧ лоӧ 0. Тайӧ кыв вожалӧм.
1901–1904-ӧд воясӧ Анри Лебег, прансуз математик, лӧсьӧдӧма выль теория. Сійӧ петкӧдлӧма, кыдзи мӧд ног позьӧ артавны эрдъяс да йӧрышъяс, а сідзжӧ функциялӧн графикувса юкӧнлысь эрдсӧ.
Лебег теория йылысь тані огӧ нин кутӧй висьтавны, пасъям сӧмын некымын результат.
1) Позьӧ кӧ артавны мыгӧрлысь эрдсӧ (йӧрышсӧ) Жордан ногӧн — позьӧ артавны и Лебег ногӧн; артмас ӧткодь лыд.
2) Кутшӧмкӧ мыгӧръяслысь эрдъяссӧ оз позь артавны Жордан ногӧн, но позьӧ артавны Лебег ногӧн. Водзын ми висьтавлім M мыгӧр йылысь (квадрат пытшкӧсса рациональ лыда координатаяса став чут). Вӧлӧмкӧ, Лебег ногӧн арталӧм эрдыс лоас 0.
3) Позьӧ кӧ артавны функциялӧн графикувса юкӧнлысь эрдсӧ Риман ногӧн, сійӧс жӧ позьӧ артавны и Лебег ногӧн; артмас ӧткодь лыд.
4) Кутшӧмсюрӧ функцияяслӧн графикувса юкӧнлысь эрдсӧ оз позь артавны Риман ногӧн, но позьӧ артавны Лебег ногӧн.
Сідзкӧ, Лебеглӧн арталан ногыс бурджык Жорданлӧн да Риманлӧн арталан ногысь: унджыктор позьӧ муртавны.
Нӧшта со мый пасъям.
5) Мед A мыгӧр торйӧдӧма A1, A2, A3, ..., An, ... мыгӧръяс вылӧ (помтӧм уна юкӧнъяс вылӧ, найӧс позьӧ нумеруйтны да сьӧрсьӧн-бӧрсьӧн гижны). Мед быд тайӧ юкӧнлысь эрдсӧ (йӧрышсӧ) позьӧ артавны Лебег ногӧн. Вӧлӧмкӧ, A-лысь эрдсӧ (йӧрышсӧ) тшӧтш позьӧ артавны Лебег ногӧн; сійӧ лоас A1, A2, A3, A4, ..., An, ... мыгӧръяслӧн эрд суммаӧн.
Лебег ассьыс теориясӧ лӧсьӧдӧма да лача кутӧма: гашкӧ, быд мыгӧрлысь эрдсӧ (йӧрышсӧ) позяс муртавны? Вӧлӧмкӧ, оз. Та вылӧ видзӧдтӧг, Лебег теория XX‐ӧд нэмся математикъяслы зэв коланаторйӧн лои.