Кыдзи оригами ногӧн ӧткодь доръяса куимпельӧса артмӧдны? — различия между версиями
Наста (сёрнитанін | чӧжӧс) (→Артмӧдӧм) |
Наста (сёрнитанін | чӧжӧс) |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 5: | Строка 5: | ||
квадрат вуж – квадратный корень | квадрат вуж – квадратный корень | ||
| − | == | + | ==Медводдза нёль аксиомаӧн вӧдитчӧмӧн артмӧдӧм== |
[[Кыдзи_оригами_ногӧн_квадрат_артмӧдны?|Ӧнтай]] квадрат лӧсьӧдігӧн параллель ногӧн гижтылім кык веськыд визь да налы перпендикуляр, а сэсся юклім ӧти веськыд пельӧссӧ биссектрисаӧн. | [[Кыдзи_оригами_ногӧн_квадрат_артмӧдны?|Ӧнтай]] квадрат лӧсьӧдігӧн параллель ногӧн гижтылім кык веськыд визь да налы перпендикуляр, а сэсся юклім ӧти веськыд пельӧссӧ биссектрисаӧн. | ||
| Строка 11: | Строка 11: | ||
[[Файл:Kuimp1.jpg|thumb|center|330px|]] | [[Файл:Kuimp1.jpg|thumb|center|330px|]] | ||
| − | Пифагор теоремаысь петӧ: AC вундӧгыс AB вундӧг серти √2 пӧв ыджыдджык (√2 — кыклӧн квадрат вуж). | + | Пифагор теоремаысь петӧ: ''AC'' вундӧгыс ''AB'' вундӧг серти √2 пӧв ыджыдджык (√2 — кыклӧн квадрат вуж). |
Сэсся со мый вӧчам. | Сэсся со мый вӧчам. | ||
| − | 1. AC визьсӧ a визь вылӧ пуктам (тайӧс позьӧ вӧчны Фудзиталӧн 3-ӧд аксиома серти); C чутлысь веськаланінсӧ пасъям K-ӧн. | + | 1. ''AC'' визьсӧ ''a'' визь вылӧ пуктам (тайӧс позьӧ вӧчны [[Оригами_геометрия|Фудзиталӧн 3-ӧд аксиома]] серти); ''C'' чутлысь веськаланінсӧ пасъям ''K''-ӧн. |
[[Файл:Kuimp2.jpg|thumb|center|330px|]] | [[Файл:Kuimp2.jpg|thumb|center|330px|]] | ||
| − | Сідзкӧ, AK вундӧгыс AB вундӧг серти √2 пӧв ыджыдджык. | + | Сідзкӧ, ''AK'' вундӧгыс ''AB'' вундӧг серти √2 пӧв ыджыдджык. |
| − | 2. K чут пыр нуӧдам a-лы перпендикуляр. Сійӧ вомӧнасяс c-кӧд ӧти чутын; пасъям сійӧс L-ӧн. Сэсся A да L чутъяс пыр нуӧдам веськыд визь (тайӧс позьӧ вӧчны Фудзиталӧн 1-ӧд аксиома серти). | + | 2. ''K'' чут пыр нуӧдам ''a''-лы перпендикуляр. Сійӧ вомӧнасяс ''c''-кӧд ӧти чутын; пасъям сійӧс ''L''-ӧн. Сэсся ''A'' да ''L'' чутъяс пыр нуӧдам веськыд визь (тайӧс позьӧ вӧчны [[Оригами_геометрия|Фудзиталӧн 1-ӧд аксиома]] серти). |
[[Файл:Kuimp3.jpg|thumb|center|330px|]] | [[Файл:Kuimp3.jpg|thumb|center|330px|]] | ||
| − | Пифагор теорема серти, AL вундӧгыс AB вундӧг серти √3 пӧв ыджыдджык. | + | Пифагор теорема серти, ''AL'' вундӧгыс ''AB'' вундӧг серти √3 пӧв ыджыдджык. |
| − | 3. AL визьсӧ a визь вылӧ пуктам; L чутлысь веськаланінсӧ пасъям M-ӧн. Сэсся M да B чутъяс пыр нуӧдам веськыд визь. | + | 3. ''AL'' визьсӧ a визь вылӧ пуктам; ''L'' чутлысь веськаланінсӧ пасъям ''M''-ӧн. Сэсся ''M'' да ''B'' чутъяс пыр нуӧдам веськыд визь. |
[[Файл:Kuimp3.jpg|thumb|center|330px|]] | [[Файл:Kuimp3.jpg|thumb|center|330px|]] | ||
| − | AM вундӧгыс AB вундӧг серти √3 пӧв ыджыдджык. Пифагор теоремаысь петӧ: BM = | + | ''AM'' вундӧгыс ''AB'' вундӧг серти √3 пӧв ыджыдджык. Пифагор теоремаысь петӧ: ''BM'' = 2''AB''. |
| − | 4. Кусыньтам кабаласӧ a визьті; B чутлысь веськаланінсӧ пасъям N-ӧн. | + | 4. Кусыньтам кабаласӧ ''a'' визьті; ''B'' чутлысь веськаланінсӧ пасъям ''N''-ӧн. |
[[Файл:Kuimp5.jpg|thumb|center|330px|]] | [[Файл:Kuimp5.jpg|thumb|center|330px|]] | ||
| − | MAB да MAN куимпельӧсаяс ӧткодьӧсь, та вӧсна BN = BM = MN = | + | ''MAB'' да ''MAN'' куимпельӧсаяс ӧткодьӧсь, та вӧсна ''BN'' = ''BM'' = ''MN'' = 2''AB''. |
| − | Сідзкӧ, BMN – ӧткодь доръяса куимпельӧса. | + | Сідзкӧ, ''BMN'' – ӧткодь доръяса куимпельӧса. |
==Пасйӧд== | ==Пасйӧд== | ||
Текущая версия на 20:33, 5 сора 2020
Терминъяс
ӧткодь доръяса куимпельӧса – равносторонний треугольник вундӧг – отрезок квадрат вуж – квадратный корень
Медводдза нёль аксиомаӧн вӧдитчӧмӧн артмӧдӧм
Ӧнтай квадрат лӧсьӧдігӧн параллель ногӧн гижтылім кык веськыд визь да налы перпендикуляр, а сэсся юклім ӧти веськыд пельӧссӧ биссектрисаӧн.
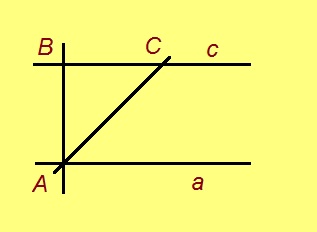
Пифагор теоремаысь петӧ: AC вундӧгыс AB вундӧг серти √2 пӧв ыджыдджык (√2 — кыклӧн квадрат вуж).
Сэсся со мый вӧчам.
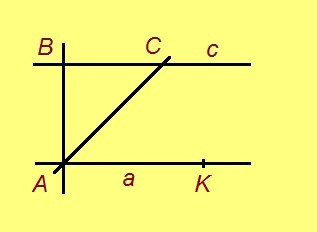
1. AC визьсӧ a визь вылӧ пуктам (тайӧс позьӧ вӧчны Фудзиталӧн 3-ӧд аксиома серти); C чутлысь веськаланінсӧ пасъям K-ӧн.
Сідзкӧ, AK вундӧгыс AB вундӧг серти √2 пӧв ыджыдджык.
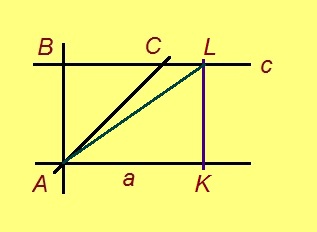
2. K чут пыр нуӧдам a-лы перпендикуляр. Сійӧ вомӧнасяс c-кӧд ӧти чутын; пасъям сійӧс L-ӧн. Сэсся A да L чутъяс пыр нуӧдам веськыд визь (тайӧс позьӧ вӧчны Фудзиталӧн 1-ӧд аксиома серти).
Пифагор теорема серти, AL вундӧгыс AB вундӧг серти √3 пӧв ыджыдджык.
3. AL визьсӧ a визь вылӧ пуктам; L чутлысь веськаланінсӧ пасъям M-ӧн. Сэсся M да B чутъяс пыр нуӧдам веськыд визь.
AM вундӧгыс AB вундӧг серти √3 пӧв ыджыдджык. Пифагор теоремаысь петӧ: BM = 2AB.
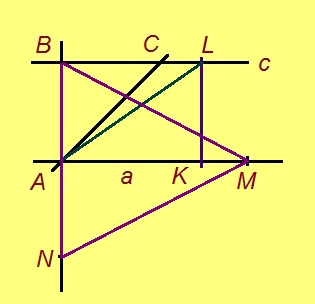
4. Кусыньтам кабаласӧ a визьті; B чутлысь веськаланінсӧ пасъям N-ӧн.
MAB да MAN куимпельӧсаяс ӧткодьӧсь, та вӧсна BN = BM = MN = 2AB.
Сідзкӧ, BMN – ӧткодь доръяса куимпельӧса.