Фудзиталӧн аксиомаяс йылысь — различия между версиями
Наста (сёрнитанін | чӧжӧс) (→Мый нӧшта артмӧдны Фудзиталӧн медводдза нёль аксиомаӧн вӧдитчӧмӧн?) |
Наста (сёрнитанін | чӧжӧс) (→Содтӧд юӧр) |
||
| (не показаны 24 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
==Терминъяс== | ==Терминъяс== | ||
| + | куимпельӧса – треугольник | ||
ӧткодь доръяса куимпельӧса – равносторонний треугольник | ӧткодь доръяса куимпельӧса – равносторонний треугольник | ||
бур унапельӧса – правильный многоугольник | бур унапельӧса – правильный многоугольник | ||
вундӧг – отрезок | вундӧг – отрезок | ||
| + | кытшвизь – окружность | ||
| + | веськыдпельӧса куимсэрӧг – прямоугольный треугольник | ||
| + | судта – высота | ||
==Фудзиталӧн аксиомаяс== | ==Фудзиталӧн аксиомаяс== | ||
| Строка 9: | Строка 13: | ||
Аксиомаяссӧ позьӧ аддзыны [[Оригами_геометрия#.D0.90.D0.BA.D1.81.D0.B8.D0.BE.D0.BC.D0.B0.D1.8F.D1.81|татысь]]. | Аксиомаяссӧ позьӧ аддзыны [[Оригами_геометрия#.D0.90.D0.BA.D1.81.D0.B8.D0.BE.D0.BC.D0.B0.D1.8F.D1.81|татысь]]. | ||
| − | ==Мый | + | ==Мый позьӧ артмӧдны Фудзиталӧн медводдза нёль аксиомаӧн вӧдитчӧмӧн?== |
Позьӧ артмӧдны [[Кыдзи_оригами_ногӧн_квадрат_артмӧдны?|квадрат]] да [[Кыдзи_оригами_ногӧн_ӧткодь_доръяса_куимпельӧса_артмӧдны?|ӧткодь доръяса куимпельӧса]]. Лӧсьӧдім кӧ квадрат да ӧткодь доръяса куимпельӧса – та бӧрын бур квайтпельӧса да бур кӧкъямыспельӧса артмӧдны абу нин сьӧкыд. | Позьӧ артмӧдны [[Кыдзи_оригами_ногӧн_квадрат_артмӧдны?|квадрат]] да [[Кыдзи_оригами_ногӧн_ӧткодь_доръяса_куимпельӧса_артмӧдны?|ӧткодь доръяса куимпельӧса]]. Лӧсьӧдім кӧ квадрат да ӧткодь доръяса куимпельӧса – та бӧрын бур квайтпельӧса да бур кӧкъямыспельӧса артмӧдны абу нин сьӧкыд. | ||
| Строка 16: | Строка 20: | ||
[[Файл:Bur unapeljesajas.jpg|thumb|center|330px|]] | [[Файл:Bur unapeljesajas.jpg|thumb|center|330px|]] | ||
| + | |||
| + | Таысь кындзи, позьӧ артмӧдны куимпельӧса, сетӧма кӧ сылысь кык дор да на костса пельӧс, либӧ ӧти дор да сы бердса кык пельӧс. | ||
Тайӧ этша на. Нёль аксиома кежысь позьӧ оз сӧмын бур унапельӧсаяссӧ артмӧдны, а и пропорциялы вундӧг корсьны. Петкӧдлам, кыдзи вӧчны тайӧс. | Тайӧ этша на. Нёль аксиома кежысь позьӧ оз сӧмын бур унапельӧсаяссӧ артмӧдны, а и пропорциялы вундӧг корсьны. Петкӧдлам, кыдзи вӧчны тайӧс. | ||
| Строка 24: | Строка 30: | ||
1. Кабаласӧ кусыньтӧмӧн артмӧдам кутшӧмкӧ пельӧс (серпасас сійӧ сьӧд рӧмӧн гижтӧма). | 1. Кабаласӧ кусыньтӧмӧн артмӧдам кутшӧмкӧ пельӧс (серпасас сійӧ сьӧд рӧмӧн гижтӧма). | ||
| + | |||
| + | [[Файл:Proporc4.jpg|thumb|center|330px|]] | ||
Пельӧс йылас пуктам ''a'', ''b'' да ''c''-лысь ӧти помнысӧ (тайӧс позьӧ вӧчны кабала кусыньтӧмӧн жӧ, 2-ӧд аксиома серти). Артмасны ''a’'' = ''a'', ''b’'' = ''b'', ''c’'' = ''c'' вундӧгъяс. | Пельӧс йылас пуктам ''a'', ''b'' да ''c''-лысь ӧти помнысӧ (тайӧс позьӧ вӧчны кабала кусыньтӧмӧн жӧ, 2-ӧд аксиома серти). Артмасны ''a’'' = ''a'', ''b’'' = ''b'', ''c’'' = ''c'' вундӧгъяс. | ||
| Строка 30: | Строка 38: | ||
2. ''a’'' да ''b’'' вундӧгъяссӧ ӧти пельӧс дор вылӧ пуктам, ''c’'' вундӧгсӧ – мӧд дор вылас (3-ӧд аксиома серти). | 2. ''a’'' да ''b’'' вундӧгъяссӧ ӧти пельӧс дор вылӧ пуктам, ''c’'' вундӧгсӧ – мӧд дор вылас (3-ӧд аксиома серти). | ||
| + | |||
| + | [[Файл:Proporc1.jpg|thumb|center|330px|]] | ||
Артмӧ: ''OA'' = ''a'', ''OB'' = ''b'', ''OC'' = ''c''. | Артмӧ: ''OA'' = ''a'', ''OB'' = ''b'', ''OC'' = ''c''. | ||
3. ''A'' да ''C'' чутъяс пыр веськыд визь нуӧдам (1-ӧд аксиома серти). Сэсся ''B'' чут пыр ''AC''-лы перпендикуляр гижтам (4-ӧд аксиома серти). Пасъям сійӧс ''k''-ӧн. Сы бӧрын ''B'' чут пыр ''k''-лы перпендикуляр нуӧдам (пасъям сійӧс m-ӧн). Миян артмӧ: ''m'' да ''AC'' – параллель нога визьяс. | 3. ''A'' да ''C'' чутъяс пыр веськыд визь нуӧдам (1-ӧд аксиома серти). Сэсся ''B'' чут пыр ''AC''-лы перпендикуляр гижтам (4-ӧд аксиома серти). Пасъям сійӧс ''k''-ӧн. Сы бӧрын ''B'' чут пыр ''k''-лы перпендикуляр нуӧдам (пасъям сійӧс m-ӧн). Миян артмӧ: ''m'' да ''AC'' – параллель нога визьяс. | ||
| + | |||
| + | [[Файл:Proporc2.jpg|thumb|center|330px|]] | ||
''OC'' да ''m'' вомӧнасьӧны ''D'' чутын. Фалес теорема серти, ''OA'' : ''OB'' = ''OC'' : ''OD'', либӧ ''a'' : ''b'' = ''c'' : ''OD''. | ''OC'' да ''m'' вомӧнасьӧны ''D'' чутын. Фалес теорема серти, ''OA'' : ''OB'' = ''OC'' : ''OD'', либӧ ''a'' : ''b'' = ''c'' : ''OD''. | ||
Со корсянторыс и сюрӧма. | Со корсянторыс и сюрӧма. | ||
| + | |||
| + | ==Мый позьӧ артмӧдны Фудзиталӧн медводдза вит аксиомаӧн вӧдитчӧмӧн?== | ||
| + | |||
| + | Ӧні петкӧдлам, мый миянлы сетас витӧд аксиомаыс. Медводз казьтыштам да гӧгӧрвоӧдам сійӧс. | ||
| + | |||
| + | Сетӧма ''A'' да ''B'' чутъяс да ''k'' веськыд визь. Витӧд аксиома серти, кабаласӧ позьӧ кусыньтны сідзи, медым ''A'' чутыс ''k'' визяс веськаліс (серпас вылас сійӧ веськалӧ ''C'' чутӧ), а кусыньтанін ''B'' чут пыр муніс. Кусыньтанін лоӧ ''AC'' вундӧглы шӧр перпендикуляр, та вӧсна ''AB'' = ''BC''. | ||
| + | |||
| + | [[Файл:Aksi1.jpg|thumb|center|330px|]] | ||
| + | |||
| + | ''B'' шӧрчута да ''AB'' радиуса кытшвизьсӧ пасъям ''w''-ӧн. Миян артмӧ: ''C'' чутыс лоӧ ''k'' веськыд визь да ''w'' кытшвизь вомӧнасянін. | ||
| + | |||
| + | [[Файл:Aksi.jpg|thumb|center|330px|]] | ||
| + | |||
| + | Дерт, витӧд аксиомасӧ колӧ стӧчмӧдны: колана кусыньтӧм эм сӧмын сэк, кор веськыд визьыс вомӧнасьӧ кытшвизьыскӧд; веськыд визьыс кӧ кытшвизьыскӧд вомӧнасьӧ кык чутын, кабаласӧ кык ногӧн позьӧ кусыньтны. | ||
| + | |||
| + | Сідзкӧ, витӧд аксиомаӧн вӧдитчӧмӧн позьӧ корсьны индӧм кытшвизьлысь да веськыд визьлысь вомӧнасян чутсӧ. Та вӧсна веськыдпельӧса куимсэрӧгсӧ сетӧм катет да гипотенуза серти лӧсьӧдны абу сьӧкыд. Петкӧдлам, кыдзи вӧчны сійӧс. Мед ''a'' – катет кузьта вундӧг, ''c'' – гипотенуза кузьта вундӧг. | ||
| + | |||
| + | 1. ''c'' вундӧглысь ӧти помсӧ ''a'' помӧ пуктам (2-ӧд аксиома серти). | ||
| + | |||
| + | 2. ''a'' вундӧглӧн мӧд пом пырыс ''h'' перпендикуляр нуӧдам (4-ӧд аксиома серти). | ||
| + | |||
| + | [[Файл:Aksi3.jpg|thumb|center|330px|]] | ||
| + | |||
| + | 3. кабаласӧ кусыньтам сідзи, медым ''A'' чут ''h''-ӧ веськаліс да кусыньтанін ''B'' чут пыр муніс (5-ӧд аксиома серти); серпас вылас ''A'' чут ''C'' чутӧ веськалӧ. Сэсся ''B'' да ''C'' чутъяс пыр веськыд визь нуӧдам. ''KBC'' – колана куимсэрӧгыс. | ||
| + | |||
| + | [[Файл:Aksi4.jpg|thumb|center|330px|]] | ||
| + | |||
| + | Подув да боквыв дор сертиыс пӧшти сэтшӧм жӧ ногӧн артмӧдӧны и ӧткодь берда куимпельӧса. Сідзкӧ, вит аксиомаӧн вӧдитчӧмӧн ӧткодь доръяса куимпельӧса позьӧ вӧчны Пифагор теоремасӧ казьтывтӧг. | ||
| + | |||
| + | Позьӧ-ӧ медводдза вит аксиома кежысь артмӧдны индӧм ''a'', ''b'' да ''c'' доръяса куимпельӧса? Вӧлӧмкӧ, позьӧ. | ||
| + | |||
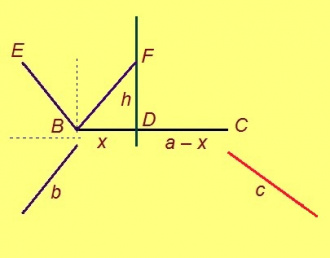
| + | Медводз со мый пасъям. Шуам, ''a'' – куимпельӧсалӧн медыджыд дорыс. Сэки сы бердса кыкнан пельӧсыс ёсьӧсь. Куимпельӧсаын ''a'' дорланьыс нуӧдӧм судтаыс юклӧ тайӧ дорсӧ ''x'' да ''a'' – ''x'' кузьта вундӧгъяс вылӧ. | ||
| + | |||
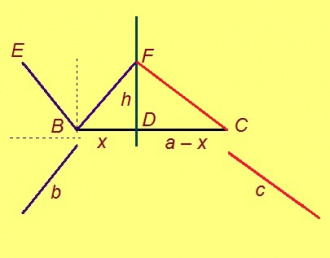
| + | [[Файл:Abc3.jpg|thumb|center|330px|]] | ||
| + | |||
| + | Артмӧдам ''x'' кузьта вундӧгсӧ. Пифагор теоремаысь позьӧ петкӧдны: ''x'' = ''a''/2 + ''b''<sup>2</sup>/2''a'' – ''c''<sup>2</sup>/2''a''. Медводдза нёль аксиоманас вӧдитчӧмӧн позьӧ содтавны, чинтавны да шӧри юклавны вундӧгъяссӧ. Сідзкӧ, миянлы колис лӧсьӧдны ''b''<sup>2</sup>/''a'' да ''c''<sup>2</sup>/''a'' кузьта вундӧгъяс. | ||
| + | |||
| + | Мед ''y'' = ''b''<sup>2</sup>/''a''. Сэки ''y'' : ''b'' = ''b'' : ''a'', либӧ ''a'' : ''b'' = ''b'' : ''y''; пропорциялы вундӧг корсьны ми кужам нин да, ''y''-сӧ артмӧдам. Сэтшӧм жӧ ногӧн ''c''<sup>2</sup>/''a'' кузьта вундӧг вӧчам. | ||
| + | |||
| + | Сідзкӧ, сетӧма ''a'', ''b'' да ''c'' вундӧгъяс. Медводз ''b''-лысь помсӧ ''a''-лӧн помӧ пуктам (2-ӧд аксиомаӧн вӧдитчӧмӧн). Сэсся лӧсьӧдам ''x'' вундӧгсӧ да пуктам сійӧс ''a'' вундӧг вылӧ, кыдзи серпасас петкӧдлӧма. | ||
| + | |||
| + | [[Файл:Abcd1.jpg|thumb|center|330px|]] | ||
| + | |||
| + | Артмӧм ''D'' чут пыр ''a'' визьлы ''h'' перпендикуляр нуӧдам (4-ӧд аксиома серти). Сы бӧрын кабаласӧ кусыньтам сідзи, медым ''E'' чут ''h'' визьӧ веськаліс да кусыньтанін ''B'' чут пыр муніс (5-ӧд аксиома серти). | ||
| + | |||
| + | [[Файл:Abcd2.jpg|thumb|center|330px|]] | ||
| + | |||
| + | ''C'' да ''F'' чутъяс пыр веськыд визь нуӧдам. Корсян куимпельӧсаыс лӧсьӧдӧма. | ||
| + | |||
| + | [[Файл:Abcd3.jpg|thumb|center|330px|]] | ||
| + | |||
| + | Сідзкӧ, куимпельӧсасӧ позьӧ лӧсьӧдны куим дор сертиыс. Та вӧсна, сетӧма кӧ кык кытшвизьлысь шӧрчутъясыс да радиусъясыс, Фудзиталӧн медводдза вит аксиомаӧн вӧдитчӧмӧн позьӧ налысь вомӧнасян чутъяссӧ корсьны. Таысь кындзи, ми вермам индӧм кытшвизьлысь да веськыд визьлысь вомӧнасянін корсьны да кык чут пыр веськыд визь нуӧдны. Мӧд ног кӧ шуны, позьӧ артмӧдны ставсӧ, мый вӧчӧны циркульӧн да линейкаӧн отсӧгӧн (кытшвизьяс гижталӧмысь кындзи). | ||
==Пасйӧд== | ==Пасйӧд== | ||
| Строка 43: | Строка 107: | ||
==Содтӧд юӧр== | ==Содтӧд юӧр== | ||
| − | [https://lovziem.blogspot.com/2020/06/blog-post_6.html Велӧдӧм паськӧдан блогын - 1.] | + | [https://lovziem.blogspot.com/2020/06/blog-post_6.html Велӧдӧм паськӧдан блогын - 1.] |
| + | [https://lovziem.blogspot.com/2020/06/1.html Велӧдӧм паськӧдан блогын - 2.] | ||
| + | [https://lovziem.blogspot.com/2020/06/2.html Велӧдӧм паськӧдан блогын - 3.] | ||
[[Category:Математика]] | [[Category:Математика]] | ||
Текущая версия на 21:57, 5 сора 2020
Содержание
Терминъяс
куимпельӧса – треугольник ӧткодь доръяса куимпельӧса – равносторонний треугольник бур унапельӧса – правильный многоугольник вундӧг – отрезок кытшвизь – окружность веськыдпельӧса куимсэрӧг – прямоугольный треугольник судта – высота
Фудзиталӧн аксиомаяс
Аксиомаяссӧ позьӧ аддзыны татысь.
Мый позьӧ артмӧдны Фудзиталӧн медводдза нёль аксиомаӧн вӧдитчӧмӧн?
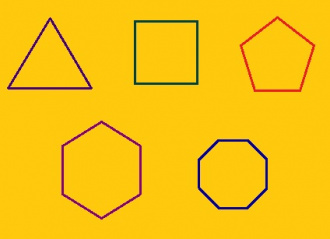
Позьӧ артмӧдны квадрат да ӧткодь доръяса куимпельӧса. Лӧсьӧдім кӧ квадрат да ӧткодь доръяса куимпельӧса – та бӧрын бур квайтпельӧса да бур кӧкъямыспельӧса артмӧдны абу нин сьӧкыд.
Дай бур витпельӧса тшӧтш позьӧ лӧсьӧдны куш нёль аксиоманас вӧдитчӧмӧн.
Таысь кындзи, позьӧ артмӧдны куимпельӧса, сетӧма кӧ сылысь кык дор да на костса пельӧс, либӧ ӧти дор да сы бердса кык пельӧс.
Тайӧ этша на. Нёль аксиома кежысь позьӧ оз сӧмын бур унапельӧсаяссӧ артмӧдны, а и пропорциялы вундӧг корсьны. Петкӧдлам, кыдзи вӧчны тайӧс.
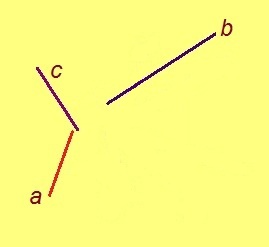
Тшӧтшкӧс вылын куим вундӧг гижтӧма: a, b, c. Колӧ артмӧдны нёльӧд вундӧг (пасъям сійӧс x-ӧн), медым a : b = c : x.
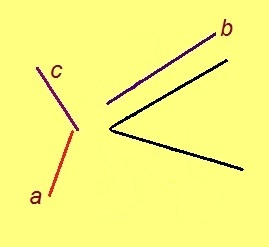
1. Кабаласӧ кусыньтӧмӧн артмӧдам кутшӧмкӧ пельӧс (серпасас сійӧ сьӧд рӧмӧн гижтӧма).
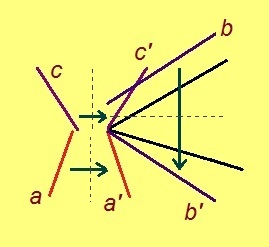
Пельӧс йылас пуктам a, b да c-лысь ӧти помнысӧ (тайӧс позьӧ вӧчны кабала кусыньтӧмӧн жӧ, 2-ӧд аксиома серти). Артмасны a’ = a, b’ = b, c’ = c вундӧгъяс.
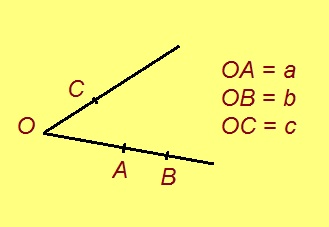
2. a’ да b’ вундӧгъяссӧ ӧти пельӧс дор вылӧ пуктам, c’ вундӧгсӧ – мӧд дор вылас (3-ӧд аксиома серти).
Артмӧ: OA = a, OB = b, OC = c.
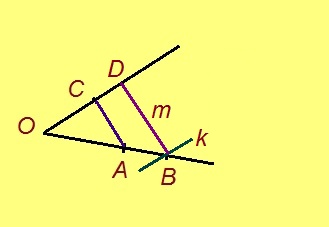
3. A да C чутъяс пыр веськыд визь нуӧдам (1-ӧд аксиома серти). Сэсся B чут пыр AC-лы перпендикуляр гижтам (4-ӧд аксиома серти). Пасъям сійӧс k-ӧн. Сы бӧрын B чут пыр k-лы перпендикуляр нуӧдам (пасъям сійӧс m-ӧн). Миян артмӧ: m да AC – параллель нога визьяс.
OC да m вомӧнасьӧны D чутын. Фалес теорема серти, OA : OB = OC : OD, либӧ a : b = c : OD.
Со корсянторыс и сюрӧма.
Мый позьӧ артмӧдны Фудзиталӧн медводдза вит аксиомаӧн вӧдитчӧмӧн?
Ӧні петкӧдлам, мый миянлы сетас витӧд аксиомаыс. Медводз казьтыштам да гӧгӧрвоӧдам сійӧс.
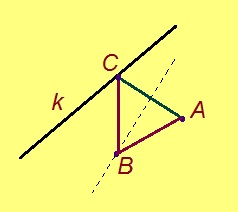
Сетӧма A да B чутъяс да k веськыд визь. Витӧд аксиома серти, кабаласӧ позьӧ кусыньтны сідзи, медым A чутыс k визяс веськаліс (серпас вылас сійӧ веськалӧ C чутӧ), а кусыньтанін B чут пыр муніс. Кусыньтанін лоӧ AC вундӧглы шӧр перпендикуляр, та вӧсна AB = BC.
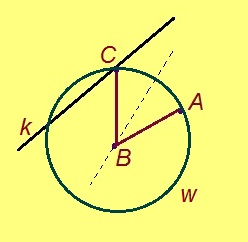
B шӧрчута да AB радиуса кытшвизьсӧ пасъям w-ӧн. Миян артмӧ: C чутыс лоӧ k веськыд визь да w кытшвизь вомӧнасянін.
Дерт, витӧд аксиомасӧ колӧ стӧчмӧдны: колана кусыньтӧм эм сӧмын сэк, кор веськыд визьыс вомӧнасьӧ кытшвизьыскӧд; веськыд визьыс кӧ кытшвизьыскӧд вомӧнасьӧ кык чутын, кабаласӧ кык ногӧн позьӧ кусыньтны.
Сідзкӧ, витӧд аксиомаӧн вӧдитчӧмӧн позьӧ корсьны индӧм кытшвизьлысь да веськыд визьлысь вомӧнасян чутсӧ. Та вӧсна веськыдпельӧса куимсэрӧгсӧ сетӧм катет да гипотенуза серти лӧсьӧдны абу сьӧкыд. Петкӧдлам, кыдзи вӧчны сійӧс. Мед a – катет кузьта вундӧг, c – гипотенуза кузьта вундӧг.
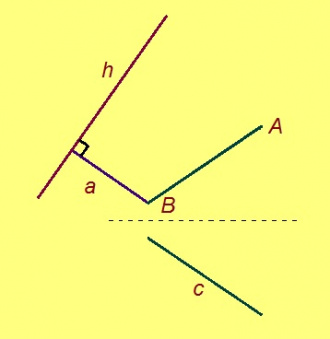
1. c вундӧглысь ӧти помсӧ a помӧ пуктам (2-ӧд аксиома серти).
2. a вундӧглӧн мӧд пом пырыс h перпендикуляр нуӧдам (4-ӧд аксиома серти).
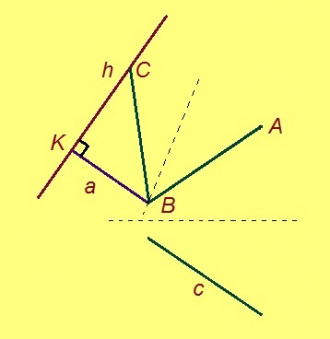
3. кабаласӧ кусыньтам сідзи, медым A чут h-ӧ веськаліс да кусыньтанін B чут пыр муніс (5-ӧд аксиома серти); серпас вылас A чут C чутӧ веськалӧ. Сэсся B да C чутъяс пыр веськыд визь нуӧдам. KBC – колана куимсэрӧгыс.
Подув да боквыв дор сертиыс пӧшти сэтшӧм жӧ ногӧн артмӧдӧны и ӧткодь берда куимпельӧса. Сідзкӧ, вит аксиомаӧн вӧдитчӧмӧн ӧткодь доръяса куимпельӧса позьӧ вӧчны Пифагор теоремасӧ казьтывтӧг.
Позьӧ-ӧ медводдза вит аксиома кежысь артмӧдны индӧм a, b да c доръяса куимпельӧса? Вӧлӧмкӧ, позьӧ.
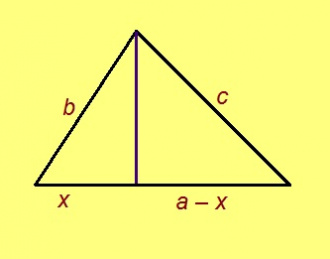
Медводз со мый пасъям. Шуам, a – куимпельӧсалӧн медыджыд дорыс. Сэки сы бердса кыкнан пельӧсыс ёсьӧсь. Куимпельӧсаын a дорланьыс нуӧдӧм судтаыс юклӧ тайӧ дорсӧ x да a – x кузьта вундӧгъяс вылӧ.
Артмӧдам x кузьта вундӧгсӧ. Пифагор теоремаысь позьӧ петкӧдны: x = a/2 + b2/2a – c2/2a. Медводдза нёль аксиоманас вӧдитчӧмӧн позьӧ содтавны, чинтавны да шӧри юклавны вундӧгъяссӧ. Сідзкӧ, миянлы колис лӧсьӧдны b2/a да c2/a кузьта вундӧгъяс.
Мед y = b2/a. Сэки y : b = b : a, либӧ a : b = b : y; пропорциялы вундӧг корсьны ми кужам нин да, y-сӧ артмӧдам. Сэтшӧм жӧ ногӧн c2/a кузьта вундӧг вӧчам.
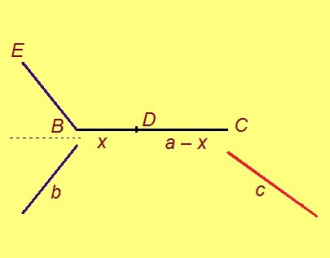
Сідзкӧ, сетӧма a, b да c вундӧгъяс. Медводз b-лысь помсӧ a-лӧн помӧ пуктам (2-ӧд аксиомаӧн вӧдитчӧмӧн). Сэсся лӧсьӧдам x вундӧгсӧ да пуктам сійӧс a вундӧг вылӧ, кыдзи серпасас петкӧдлӧма.
Артмӧм D чут пыр a визьлы h перпендикуляр нуӧдам (4-ӧд аксиома серти). Сы бӧрын кабаласӧ кусыньтам сідзи, медым E чут h визьӧ веськаліс да кусыньтанін B чут пыр муніс (5-ӧд аксиома серти).
C да F чутъяс пыр веськыд визь нуӧдам. Корсян куимпельӧсаыс лӧсьӧдӧма.
Сідзкӧ, куимпельӧсасӧ позьӧ лӧсьӧдны куим дор сертиыс. Та вӧсна, сетӧма кӧ кык кытшвизьлысь шӧрчутъясыс да радиусъясыс, Фудзиталӧн медводдза вит аксиомаӧн вӧдитчӧмӧн позьӧ налысь вомӧнасян чутъяссӧ корсьны. Таысь кындзи, ми вермам индӧм кытшвизьлысь да веськыд визьлысь вомӧнасянін корсьны да кык чут пыр веськыд визь нуӧдны. Мӧд ног кӧ шуны, позьӧ артмӧдны ставсӧ, мый вӧчӧны циркульӧн да линейкаӧн отсӧгӧн (кытшвизьяс гижталӧмысь кындзи).
Пасйӧд
Содтӧд юӧр
Велӧдӧм паськӧдан блогын - 1. Велӧдӧм паськӧдан блогын - 2. Велӧдӧм паськӧдан блогын - 3.