Комплекс лыдъяс — различия между версиями
Наста (сёрнитанін | чӧжӧс) (→...Вайӧй жӧ перъям да выль лыдъяс артмӧдам!) |
Наста (сёрнитанін | чӧжӧс) (→Геометрия боксянь гӧгӧрвоӧдӧм) |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 31: | Строка 31: | ||
Медводз минуса лыдысь квадрат вуж йылысь гижӧма италияса математик Джероламо Кардано "Ыджыд кужӧг" трактатын (Ars magna, 1545). Сійӧ со кутшӧм задача видлалӧма: колӧ корсьны кык лыд, медым налӧн суммаыс вӧлі 10, а лыдмӧдасыс вӧлі 40. Арталӧма да со кутшӧм лыдъяс артмӧдӧма: 5 + √(−15) да 5 − √(−15). На йылысь Кардано пасйӧма: "Тайӧ дзуг ыдждаясыс ковтӧмӧсь, кӧть и зэв аслыспӧлӧсӧсь". Сэсся лыдмӧдӧма найӧс да артмӧдӧма 25 − (−15) = 25 + 15 = 40. | Медводз минуса лыдысь квадрат вуж йылысь гижӧма италияса математик Джероламо Кардано "Ыджыд кужӧг" трактатын (Ars magna, 1545). Сійӧ со кутшӧм задача видлалӧма: колӧ корсьны кык лыд, медым налӧн суммаыс вӧлі 10, а лыдмӧдасыс вӧлі 40. Арталӧма да со кутшӧм лыдъяс артмӧдӧма: 5 + √(−15) да 5 − √(−15). На йылысь Кардано пасйӧма: "Тайӧ дзуг ыдждаясыс ковтӧмӧсь, кӧть и зэв аслыспӧлӧсӧсь". Сэсся лыдмӧдӧма найӧс да артмӧдӧма 25 − (−15) = 25 + 15 = 40. | ||
| + | |||
| + | [[Файл:Page 66.jpg|thumb|center|220px|]] | ||
Сёрӧнджык Кардано бара татшӧм лыдъясӧ "зурасьӧма". Сійӧ лӧсьӧдӧма куб ӧткодьлунлысь вужъяс корсян формула. Артмӧма тадз: ӧткодьлуныслӧн кӧ эм куим вуж, формулаас эм минуса лыдысь квадрат вуж. Мый водзӧ вӧчны тайӧ формуланас, Кардано эз тӧд. | Сёрӧнджык Кардано бара татшӧм лыдъясӧ "зурасьӧма". Сійӧ лӧсьӧдӧма куб ӧткодьлунлысь вужъяс корсян формула. Артмӧма тадз: ӧткодьлуныслӧн кӧ эм куим вуж, формулаас эм минуса лыдысь квадрат вуж. Мый водзӧ вӧчны тайӧ формуланас, Кардано эз тӧд. | ||
| Строка 76: | Строка 78: | ||
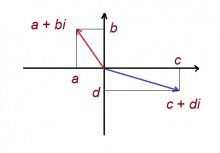
Тшӧтшкӧс вылын бӧръям координата система. Мед ''a'' + ''bi'' — комплекс лыд (''a'' да ''b'' — ина лыдъяс, ''i'' = √(−1) — интӧм ӧтик). Пуктам тшӧтшкӧс вылас ''a'' абсциссаа да ''b'' ординатаа чут. Сідзкӧ, быд комплекс лыдлы лӧсялӧ тшӧтшкӧсвывса чут (либӧ радиус-вектор). | Тшӧтшкӧс вылын бӧръям координата система. Мед ''a'' + ''bi'' — комплекс лыд (''a'' да ''b'' — ина лыдъяс, ''i'' = √(−1) — интӧм ӧтик). Пуктам тшӧтшкӧс вылас ''a'' абсциссаа да ''b'' ординатаа чут. Сідзкӧ, быд комплекс лыдлы лӧсялӧ тшӧтшкӧсвывса чут (либӧ радиус-вектор). | ||
| + | |||
| + | [[Файл:Compl coord.jpg|thumb|center|220px|]] | ||
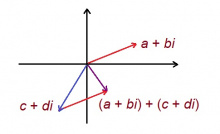
Казьтыштам: ''a'' + ''bi'' да ''c'' + ''di'' лыдъяслӧн суммаыс лоӧ | Казьтыштам: ''a'' + ''bi'' да ''c'' + ''di'' лыдъяслӧн суммаыс лоӧ | ||
| Строка 82: | Строка 86: | ||
Тшӧтшкӧсвывса чутъясыслӧн со кутшӧм координатаяс: (''a'', ''b'') да (''c'', ''d''); суммаыслӧн (''a'' + ''c'', ''b'' + ''d''). Сідзкӧ, артмӧ радиус-векторъясыслӧн сумма. | Тшӧтшкӧсвывса чутъясыслӧн со кутшӧм координатаяс: (''a'', ''b'') да (''c'', ''d''); суммаыслӧн (''a'' + ''c'', ''b'' + ''d''). Сідзкӧ, артмӧ радиус-векторъясыслӧн сумма. | ||
| + | |||
| + | [[Файл:Compl sum.jpg|thumb|center|220px|]] | ||
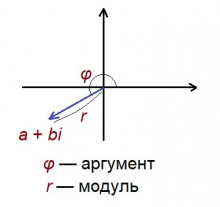
Сетӧма кӧ (''a'', ''b'') координатаяса радиус-вектор, позьӧ муртавны сылысь кузьтасӧ да тӧдмавны, кутшӧм пельӧс сійӧ артмӧдӧ абсцисса чӧрскӧд (0°-сянь 360°-ӧдз, либӧ 0-сянь 2''π''-ӧдз). Кузьтаыс шусьӧ ''a'' + ''bi'' лыдлӧн модульӧн, а пельӧсыс шусьӧ сылӧн аргументӧн. | Сетӧма кӧ (''a'', ''b'') координатаяса радиус-вектор, позьӧ муртавны сылысь кузьтасӧ да тӧдмавны, кутшӧм пельӧс сійӧ артмӧдӧ абсцисса чӧрскӧд (0°-сянь 360°-ӧдз, либӧ 0-сянь 2''π''-ӧдз). Кузьтаыс шусьӧ ''a'' + ''bi'' лыдлӧн модульӧн, а пельӧсыс шусьӧ сылӧн аргументӧн. | ||
| + | |||
| + | [[Файл:Mod arg.jpg|thumb|center|220px|]] | ||
Пифагор теоремаысь тыдовтчӧ: модульлӧн квадрат лоӧ ''a''² + ''b''². | Пифагор теоремаысь тыдовтчӧ: модульлӧн квадрат лоӧ ''a''² + ''b''². | ||
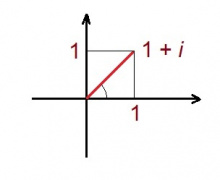
'''Видлӧг.''' 1 + ''i'' лыдлы лӧсялӧ (1, 1) координатаа радиус-вектор. Сійӧ артмӧдӧ 45° (либӧ ''π''/4) пельӧс абсцисса чӧрскӧд. Кузьтаыс лоӧ √2 (кыкысь квадрат вуж). Сідзкӧ, аргумент лоӧ ''π''/4, модуль лоӧ √2. | '''Видлӧг.''' 1 + ''i'' лыдлы лӧсялӧ (1, 1) координатаа радиус-вектор. Сійӧ артмӧдӧ 45° (либӧ ''π''/4) пельӧс абсцисса чӧрскӧд. Кузьтаыс лоӧ √2 (кыкысь квадрат вуж). Сідзкӧ, аргумент лоӧ ''π''/4, модуль лоӧ √2. | ||
| + | |||
| + | [[Файл:1 plus i.jpg|thumb|center|220px|]] | ||
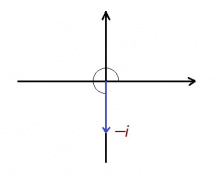
'''Видлӧг.''' −''i'' лыдлы лӧсялӧ (0, −1) координатаа радиус-вектор. Сійӧ артмӧдӧ 270° (либӧ 3''π''/2) пельӧс абсцисса чӧрскӧд. Кузьтаыс лоӧ 1. Сідзкӧ, аргумент лоӧ 3''π''/2, модуль лоӧ 1. | '''Видлӧг.''' −''i'' лыдлы лӧсялӧ (0, −1) координатаа радиус-вектор. Сійӧ артмӧдӧ 270° (либӧ 3''π''/2) пельӧс абсцисса чӧрскӧд. Кузьтаыс лоӧ 1. Сідзкӧ, аргумент лоӧ 3''π''/2, модуль лоӧ 1. | ||
| + | |||
| + | [[Файл:Minus i.jpg|thumb|center|220px|]] | ||
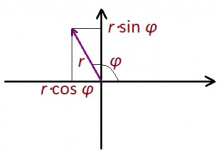
Мед ''a'' + ''bi'' лыдлӧн модуль лоӧ ''r'', а аргумент лоӧ ''φ''. Сэки | Мед ''a'' + ''bi'' лыдлӧн модуль лоӧ ''r'', а аргумент лоӧ ''φ''. Сэки | ||
''a'' = ''r''⋅cos ''φ'', ''b'' = ''r''⋅sin ''φ''. | ''a'' = ''r''⋅cos ''φ'', ''b'' = ''r''⋅sin ''φ''. | ||
| + | |||
| + | [[Файл:R.jpg|thumb|center|220px|]] | ||
Мый артмӧ, лыдмӧдам кӧ комплекс кык лыд? Казьтыштам: | Мый артмӧ, лыдмӧдам кӧ комплекс кык лыд? Казьтыштам: | ||
| Строка 116: | Строка 130: | ||
Сідзкӧ, медым лыдмӧдны комплекс кык лыд, колӧ лыдмӧдны налысь модульяссӧ да содтыны налысь аргументъяссӧ. | Сідзкӧ, медым лыдмӧдны комплекс кык лыд, колӧ лыдмӧдны налысь модульяссӧ да содтыны налысь аргументъяссӧ. | ||
| + | |||
| + | [[Файл:Compl lydm.jpg|thumb|center|220px|]] | ||
==Содтӧд юӧр== | ==Содтӧд юӧр== | ||
Текущая версия на 21:10, 2 рака 2022
Содержание
Терминъяс
минуса лыд — отрицательное число плюса лыд — положительное число минустӧм лыд — неотрицательное число квадрат вуж — квадратный корень куб вуж — кубический корень лыдмӧдны — умножить лыдмӧдас — произведение куб ӧткодьлун — кубическое уравнение куб ӧткодьлунлӧн вуж — корень кубического уравнения тшӧтшкӧс — плоскость ина лыд — вещественное число интӧм ӧтик — мнимая единица лыдмӧдас — произведение
Минуса лыдысь квадрат вуж перйыны оз позь
Школаын ми велӧдлім: "минуссӧ" кӧ "минус" пӧв босьтам, лоас "плюс" (лыдмӧдам кӧ кык минуса лыд, артмас плюса лыд). Лыдмӧдам кӧ кык плюса лыд, бара артмас плюса лыд. Та вӧсна быд лыдлӧн квадрат лоас минустӧм: a лыд кӧ плюса, артмас
a² = a⋅a > 0, (−a)² = (−a)⋅(−a) = a⋅a > 0, 0² = 0⋅0 = 0.
Сідзкӧ, минуса лыдысь квадрат вуж перйыны оз позь.
...Вайӧй жӧ перъям да выль лыдъяс артмӧдам!
Вӧлӧмкӧ, 16-ӧд нэмсянь математикъяс вӧдитчӧны татшӧм "абутӧм" вужъяснас. (Казьтыштам: 19-ӧд нэмӧдз весиг минуса лыдъяссӧ чайтӧмаӧсь "ылӧдчанаӧн", "лӧсявтӧмӧн".)
Медводз минуса лыдысь квадрат вуж йылысь гижӧма италияса математик Джероламо Кардано "Ыджыд кужӧг" трактатын (Ars magna, 1545). Сійӧ со кутшӧм задача видлалӧма: колӧ корсьны кык лыд, медым налӧн суммаыс вӧлі 10, а лыдмӧдасыс вӧлі 40. Арталӧма да со кутшӧм лыдъяс артмӧдӧма: 5 + √(−15) да 5 − √(−15). На йылысь Кардано пасйӧма: "Тайӧ дзуг ыдждаясыс ковтӧмӧсь, кӧть и зэв аслыспӧлӧсӧсь". Сэсся лыдмӧдӧма найӧс да артмӧдӧма 25 − (−15) = 25 + 15 = 40.
Сёрӧнджык Кардано бара татшӧм лыдъясӧ "зурасьӧма". Сійӧ лӧсьӧдӧма куб ӧткодьлунлысь вужъяс корсян формула. Артмӧма тадз: ӧткодьлуныслӧн кӧ эм куим вуж, формулаас эм минуса лыдысь квадрат вуж. Мый водзӧ вӧчны тайӧ формуланас, Кардано эз тӧд. Италияса мӧд математик, Рафаэль Бомбелли, 1572-ӧд воын индӧма, кыдзи содтавны, чинтавны, лыдмӧдавны да юклыны татшӧм аслыспӧлӧс лыдъяссӧ. Шуам, содталӧны да чинталӧны найӧс тадзи:
a + b√(−1) + c + d√(−1) = (a + c) + (b + d)√(−1), a + b√(−1) − [c + d√(−1)] = (a − c) + (b − d)√(−1).
А лыдмӧдӧны скобкаяс восьтӧмӧн, кыдзи алгебра урокъяс вылын ми велӧдлім:
[a + b√(−1)]⋅[c + d√(−1)] = ac + cb√(−1) + ad√(−1) + bd√(−1)⋅√(−1) = ac − bd + (cb + ad)√(−1).
Бомбелли видлалӧма со кутшӧм ӧткодьлун:
x³ = 15x + 4.
Сылӧн ӧти вужйыс лоӧ 4:
4³ = 64, 15⋅4 + 4 = 64.
Карданолӧн формулаяс серти, медым корсьны вужсӧ, колӧ содтыны кык лыд: ӧтиыс лоӧ 2 + 11√(−1)-ысь куб вуж, а мӧдыс лоӧ 2 − 11√(−1)-ысь куб вуж. Бомбелли гӧгӧрвоӧма: тайӧ куб вужъясыс лоӧны 2 + √(−1) да 2 − √(−1). Арталам индӧм правилӧ серти:
(2 + √(−1))³ = (2 + √(−1))(2 + √(−1))(2 + √(−1)) = (3 + 4√(−1))(2 + √(−1)) = 2 + 11√(−1), (2 − √(−1))³ = (2 − √(−1))(2 − √(−1))(2 − √(−1)) = (3 − 4√(−1))(2 − √(−1)) = 2 − 11√(−1).
Содтам кӧ 2 + √(−1) да 2 − √(−1), буретш 4 и артмас.
Ачыс Бомбелли, Кардано моз, чайтӧма √(−1)-а лыдъяссӧ ковтӧмӧн. Налӧн пӧльза йылысь пасйӧма Альбер Жирар (1595−1632), прансуз математик; сӧмын сылысь мӧвпъяссӧ дыр на пыдди эз пуктыны.
Ина, интӧм да комплекс лыдъяс
Анри Декарт пондӧма a + b√(−1) лыдъяссӧ шуны интӧмӧн (рочӧн кӧ, мнимые; англичан кывйӧн — imaginary). Сёрӧнджык терминология вежсьӧма:
- a + b√(−1) лыдсӧ ӧні шуӧны комплекс лыдӧн;
- a лыдсӧ шуӧны ина лыдӧн (вещественное число);
- b√(−1) лыдсӧ шуӧны интӧм лыдӧн (мнимое число).
Леонард Эйлер пондӧма пасъявны √(−1) лыдсӧ i шыпасӧн; i лыд шусьӧ "интӧм ӧтик" (мнимая единица). Ӧні a + b√(−1) пыдди гижӧны a + bi.
Геометрия боксянь гӧгӧрвоӧдӧм
Тшӧтшкӧс вылын бӧръям координата система. Мед a + bi — комплекс лыд (a да b — ина лыдъяс, i = √(−1) — интӧм ӧтик). Пуктам тшӧтшкӧс вылас a абсциссаа да b ординатаа чут. Сідзкӧ, быд комплекс лыдлы лӧсялӧ тшӧтшкӧсвывса чут (либӧ радиус-вектор).
Казьтыштам: a + bi да c + di лыдъяслӧн суммаыс лоӧ
a + c + (b + d)i.
Тшӧтшкӧсвывса чутъясыслӧн со кутшӧм координатаяс: (a, b) да (c, d); суммаыслӧн (a + c, b + d). Сідзкӧ, артмӧ радиус-векторъясыслӧн сумма.
Сетӧма кӧ (a, b) координатаяса радиус-вектор, позьӧ муртавны сылысь кузьтасӧ да тӧдмавны, кутшӧм пельӧс сійӧ артмӧдӧ абсцисса чӧрскӧд (0°-сянь 360°-ӧдз, либӧ 0-сянь 2π-ӧдз). Кузьтаыс шусьӧ a + bi лыдлӧн модульӧн, а пельӧсыс шусьӧ сылӧн аргументӧн.
Пифагор теоремаысь тыдовтчӧ: модульлӧн квадрат лоӧ a² + b².
Видлӧг. 1 + i лыдлы лӧсялӧ (1, 1) координатаа радиус-вектор. Сійӧ артмӧдӧ 45° (либӧ π/4) пельӧс абсцисса чӧрскӧд. Кузьтаыс лоӧ √2 (кыкысь квадрат вуж). Сідзкӧ, аргумент лоӧ π/4, модуль лоӧ √2.
Видлӧг. −i лыдлы лӧсялӧ (0, −1) координатаа радиус-вектор. Сійӧ артмӧдӧ 270° (либӧ 3π/2) пельӧс абсцисса чӧрскӧд. Кузьтаыс лоӧ 1. Сідзкӧ, аргумент лоӧ 3π/2, модуль лоӧ 1.
Мед a + bi лыдлӧн модуль лоӧ r, а аргумент лоӧ φ. Сэки
a = r⋅cos φ, b = r⋅sin φ.
Мый артмӧ, лыдмӧдам кӧ комплекс кык лыд? Казьтыштам:
(a + bi)(c + di) = ac − bd + (ad + bc)i.
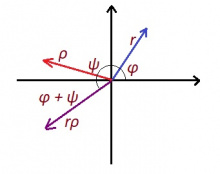
Сідзкӧ, медводдза лыдыс кӧ r модуля да φ аргумента, а мӧд лыдыс кӧ ρ модуля да ψ аргумента, налӧн лыдмӧдасыс лоӧ
rρ(cos φ⋅cos ψ − sin φ⋅sin ψ) + rρ(cos φ⋅sin ψ + sin φ⋅cos ψ)i.
Уськӧдам тӧд вылӧ тригонометрияысь формулаяс:
cos φ⋅cos ψ − sin φ⋅sin ψ = cos (φ + ψ),
cos φ⋅sin ψ + sin φ⋅cos ψ = sin (φ + ψ).
Та вӧсна лыдмӧдасыс лоӧ
rρ⋅cos (φ + ψ) + rρ⋅sin (φ + ψ)⋅i.
Сылӧн модульыс лоӧ rρ, а аргументыс лоӧ φ + ψ.
Сідзкӧ, медым лыдмӧдны комплекс кык лыд, колӧ лыдмӧдны налысь модульяссӧ да содтыны налысь аргументъяссӧ.