Жюлиалӧн чут чукӧръяс — различия между версиями
Наста (сёрнитанін | чӧжӧс) (Новая страница: «==Терминъяс== чут чукӧр — множество точек ина лыд — вещественное число интӧм ӧтик — мни…») |
Наста (сёрнитанін | чӧжӧс) (→Жюлиалӧн чут чукӧръяс) |
||
| (не показано 8 промежуточных версий этого же участника) | |||
| Строка 9: | Строка 9: | ||
==Жюлиалӧн чут чукӧръяс== | ==Жюлиалӧн чут чукӧръяс== | ||
| − | Ӧнтай ми висьтавлім комплекс лыдъяс йылысь: тайӧ ''a'' + ''bi'' лыдъяс, кӧні a да b — ина лыдъяс, i = √(−1) — интӧм ӧтик; a + bi лыдлы лӧсялӧ тшӧтшкӧсвывса (a, b) координатаяса чут. | + | [[Комплекс_лыдъяс|Ӧнтай]] ми висьтавлім комплекс лыдъяс йылысь: тайӧ ''a'' + ''bi'' лыдъяс, кӧні ''a'' да ''b'' — ина лыдъяс, ''i'' = √(−1) — интӧм ӧтик; ''a'' + ''bi'' лыдлы лӧсялӧ тшӧтшкӧсвывса (''a'', ''b'') координатаяса чут. |
Ӧні висьталам, кыдзи артмӧны тшӧтшкӧс вылас зэв мича да дзуг серпасъяс — Жюлиалӧн чут чукӧръяс (став серпасыс босьтӧма ӧтуввезйысь). | Ӧні висьталам, кыдзи артмӧны тшӧтшкӧс вылас зэв мича да дзуг серпасъяс — Жюлиалӧн чут чукӧръяс (став серпасыс босьтӧма ӧтуввезйысь). | ||
| − | + | [[Файл:800px-Julia set (highres 02).jpg|thumb|center|220px|]] | |
| − | + | Мед ''c'' да ''z'' — кутшӧмкӧ комплекс лыдъяс. Пондам артмӧдны сьӧрсьӧн-бӧрсьӧн ''zₙ'' лыдъяс: ''z''₀ = ''z'', ''z''₁ = ''z''₀² + ''c'', ''z''₂ = ''z''₁² + ''c'', ''z''₃ = ''z''₂² + ''c'', ''z''₄ = ''z''₃² + ''c'' да с. в. | |
| − | Казялам: r лыд кӧ зэв ыджыд (кутшӧмкӧ R лыдысь ыджыдджык), | + | Ӧтластитам ''zₙ'' да ''zₙ''₊₁ лыдъяслысь модульяссӧ (казьтыштам: a + bi лыдлӧн модуль — тайӧ (a, b) радиус-векторлӧн кузьта). Мед |''zₙ''| = ''r''. [[Комплекс_лыдъяс|Воддза гижӧд серти]], |''zₙ''²| = |''zₙ''|² = ''r''². Куимпельӧса ӧткодьтӧмлунысь артмӧ: |''zₙ''₊₁| = |''zₙ''² + ''c''| ≥ |''zₙ''²| − |''c''| = ''r''² − |''c''|. |
| + | |||
| + | [[Файл:Zzc.jpg|thumb|center|220px|]] | ||
| + | |||
| + | Казялам: ''r'' лыд кӧ зэв ыджыд (кутшӧмкӧ ''R'' лыдысь ыджыдджык), ''r''² − |''c''| ≥ 2''r''. Сідзкӧ, |''zₙ''₊₁| ≥ 2|''zₙ''| ≥ 2''R''. Но сэки миян артмӧ: |''zₙ''₊₂| ≥ 2|''zₙ''₊₁| ≥ 4|''zₙ''|, |''zₙ''₊₃| ≥ 2|''zₙ''₊₂| ≥ 8|''zₙ''| да с. в.; ''k'' лыд помтӧг содігас |''zₙ''₊''ₖ''| тшӧтш кутас помтӧг быдмыны. | ||
Сідзкӧ, вермӧ лоны кык вариант: | Сідзкӧ, вермӧ лоны кык вариант: | ||
| − | 1) либӧ став zₙ лыд чукӧр куйлӧ R радиуса кытшын, | + | 1) либӧ став ''zₙ'' лыд чукӧр куйлӧ ''R'' радиуса кытшын, |
| − | 2) либӧ кутшӧмкӧ здуксянь |zₙ| заводитӧны помтӧг быдмыны. | + | 2) либӧ кутшӧмкӧ здуксянь |''zₙ''| заводитӧны помтӧг быдмыны. |
| + | |||
| + | Видлалам медводдза случайлы лӧсялысь став ''z'' лыдсӧ: кор ''z'', ''z''² + ''c'', (''z''² + ''c'')² + ''c'' да с. в. куйлӧны ''R'' радиуса кытшын. Тшӧтшкӧс вылын артмӧ кутшӧмкӧ мыгӧр. Сылӧн вежтасыс и шусьӧ Жюлиалӧн чут чукӧрӧн. (Гастон Жюлиа — прансуз математик, 1893−1978.) | ||
| − | + | '''Видлӧг.''' Мед ''c'' = 0. Сэки ''z''₀ = ''z'', ''z''₁ = ''z''², ''z''₂ = ''z''⁴, ''z''₃ = ''z''⁸, ''z''₄ = ''z''¹⁶ да с. в. Сідзкӧ, кор |''z''| > 1, |''zₙ''| помтӧг быдмӧны; кор |''z''| ≤ 1, став ''zₙ'' куйлӧны 1 радиуса кытшын. Тайӧ кытшыслӧн вежтас — 1 радиуса кытшвизь. Миян артмис: кор ''c'' = 0, Жюлиалӧн чут чукӧрӧн лоас 1 радиуса кытшвизь. | |
| − | + | Босьтам кӧ кутшӧмкӧ мӧд ''c'' лыдсӧ, Жюлиалӧн чут чукӧр вермӧ лоны зэв аслыспӧлӧсӧн да дзугӧн. Серпас вылас петкӧдлӧма ӧти пример: ''c'' = 0,28+0,0113''i''; ''z'' лыд кӧ куйлӧ югыдлӧз юкӧнын, |''zₙ''| помтӧг быдмӧны; ''z'' лыд кӧ куйлӧ гӧрд юкӧнын, став ''zₙ'' куйлӧ кутшӧмкӧ кытшын; гӧрд мыгӧрлӧн вежтасыс — Жюлиалӧн чут чукӧр. | |
| − | + | [[Файл:Julia028+0,0113i.png|thumb|center|220px|]] | |
Вӧлӧмкӧ, видзӧдлам кӧ вежтасыслӧн ичӧт юкӧн вылас лупа пыр, бара аддзам сэтысь дзуг структура. Позьӧ водзӧ ичӧтмӧдны тайӧ юкӧнъяссӧ да босьтны ёнджык лупаяс — дзуг структурасӧ пыр аддзам. Татшӧм аслыссикас мыгӧръяс шусьӧны фракталъясӧн. | Вӧлӧмкӧ, видзӧдлам кӧ вежтасыслӧн ичӧт юкӧн вылас лупа пыр, бара аддзам сэтысь дзуг структура. Позьӧ водзӧ ичӧтмӧдны тайӧ юкӧнъяссӧ да босьтны ёнджык лупаяс — дзуг структурасӧ пыр аддзам. Татшӧм аслыссикас мыгӧръяс шусьӧны фракталъясӧн. | ||
| Строка 34: | Строка 40: | ||
Петкӧдлам нӧшта некымын пример. | Петкӧдлам нӧшта некымын пример. | ||
| − | 1) c = i. Артмӧ чардби сяма мыгӧр. | + | 1) ''c'' = ''i''. Артмӧ чардби сяма мыгӧр. |
| + | |||
| + | [[Файл:Julia i.jpg|thumb|center|220px|]] | ||
| − | 2) c = −0.765 + 0. | + | 2) ''c'' = −0.765 + 0.12''i''. |
| − | + | [[Файл:Julia compl.jpg|thumb|center|220px|]] | |
| − | 4) c = −0.70176 − 0. | + | 3) ''c'' = − 1.75488... |
| + | |||
| + | [[Файл:Julia 1 75488.jpg|thumb|center|220px|]] | ||
| + | |||
| + | 4) ''c'' = −0.70176 − 0.3842''i''. | ||
| + | |||
| + | [[Файл:Julia -0.70176 -0.3842.png|thumb|center|220px|]] | ||
А со — серпасъясысь таблича. | А со — серпасъясысь таблича. | ||
| + | |||
| + | [[Файл:Julia-Teppich.png|thumb|center|220px|]] | ||
| + | |||
| + | ==Содтӧд юӧр== | ||
| + | |||
| + | [http://lovziem.blogspot.com/2022/01/blog-post.html Велӧдӧм паськӧдан блогын] | ||
| + | |||
| + | [[Category:Математика]] | ||
Текущая версия на 21:49, 2 рака 2022
Терминъяс
чут чукӧр — множество точек ина лыд — вещественное число интӧм ӧтик — мнимая единица тшӧтшкӧс — плоскость куимпельӧса ӧткодьтӧмлун — неравенство треугольника вежтас — граница
Жюлиалӧн чут чукӧръяс
Ӧнтай ми висьтавлім комплекс лыдъяс йылысь: тайӧ a + bi лыдъяс, кӧні a да b — ина лыдъяс, i = √(−1) — интӧм ӧтик; a + bi лыдлы лӧсялӧ тшӧтшкӧсвывса (a, b) координатаяса чут.
Ӧні висьталам, кыдзи артмӧны тшӧтшкӧс вылас зэв мича да дзуг серпасъяс — Жюлиалӧн чут чукӧръяс (став серпасыс босьтӧма ӧтуввезйысь).
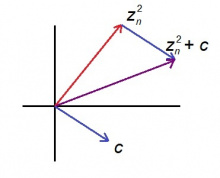
Мед c да z — кутшӧмкӧ комплекс лыдъяс. Пондам артмӧдны сьӧрсьӧн-бӧрсьӧн zₙ лыдъяс: z₀ = z, z₁ = z₀² + c, z₂ = z₁² + c, z₃ = z₂² + c, z₄ = z₃² + c да с. в.
Ӧтластитам zₙ да zₙ₊₁ лыдъяслысь модульяссӧ (казьтыштам: a + bi лыдлӧн модуль — тайӧ (a, b) радиус-векторлӧн кузьта). Мед |zₙ| = r. Воддза гижӧд серти, |zₙ²| = |zₙ|² = r². Куимпельӧса ӧткодьтӧмлунысь артмӧ: |zₙ₊₁| = |zₙ² + c| ≥ |zₙ²| − |c| = r² − |c|.
Казялам: r лыд кӧ зэв ыджыд (кутшӧмкӧ R лыдысь ыджыдджык), r² − |c| ≥ 2r. Сідзкӧ, |zₙ₊₁| ≥ 2|zₙ| ≥ 2R. Но сэки миян артмӧ: |zₙ₊₂| ≥ 2|zₙ₊₁| ≥ 4|zₙ|, |zₙ₊₃| ≥ 2|zₙ₊₂| ≥ 8|zₙ| да с. в.; k лыд помтӧг содігас |zₙ₊ₖ| тшӧтш кутас помтӧг быдмыны.
Сідзкӧ, вермӧ лоны кык вариант:
1) либӧ став zₙ лыд чукӧр куйлӧ R радиуса кытшын, 2) либӧ кутшӧмкӧ здуксянь |zₙ| заводитӧны помтӧг быдмыны.
Видлалам медводдза случайлы лӧсялысь став z лыдсӧ: кор z, z² + c, (z² + c)² + c да с. в. куйлӧны R радиуса кытшын. Тшӧтшкӧс вылын артмӧ кутшӧмкӧ мыгӧр. Сылӧн вежтасыс и шусьӧ Жюлиалӧн чут чукӧрӧн. (Гастон Жюлиа — прансуз математик, 1893−1978.)
Видлӧг. Мед c = 0. Сэки z₀ = z, z₁ = z², z₂ = z⁴, z₃ = z⁸, z₄ = z¹⁶ да с. в. Сідзкӧ, кор |z| > 1, |zₙ| помтӧг быдмӧны; кор |z| ≤ 1, став zₙ куйлӧны 1 радиуса кытшын. Тайӧ кытшыслӧн вежтас — 1 радиуса кытшвизь. Миян артмис: кор c = 0, Жюлиалӧн чут чукӧрӧн лоас 1 радиуса кытшвизь.
Босьтам кӧ кутшӧмкӧ мӧд c лыдсӧ, Жюлиалӧн чут чукӧр вермӧ лоны зэв аслыспӧлӧсӧн да дзугӧн. Серпас вылас петкӧдлӧма ӧти пример: c = 0,28+0,0113i; z лыд кӧ куйлӧ югыдлӧз юкӧнын, |zₙ| помтӧг быдмӧны; z лыд кӧ куйлӧ гӧрд юкӧнын, став zₙ куйлӧ кутшӧмкӧ кытшын; гӧрд мыгӧрлӧн вежтасыс — Жюлиалӧн чут чукӧр.
Вӧлӧмкӧ, видзӧдлам кӧ вежтасыслӧн ичӧт юкӧн вылас лупа пыр, бара аддзам сэтысь дзуг структура. Позьӧ водзӧ ичӧтмӧдны тайӧ юкӧнъяссӧ да босьтны ёнджык лупаяс — дзуг структурасӧ пыр аддзам. Татшӧм аслыссикас мыгӧръяс шусьӧны фракталъясӧн.
Петкӧдлам нӧшта некымын пример.
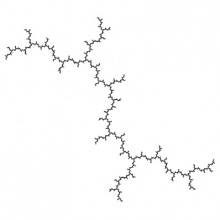
1) c = i. Артмӧ чардби сяма мыгӧр.
2) c = −0.765 + 0.12i.
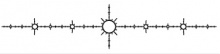
3) c = − 1.75488...
4) c = −0.70176 − 0.3842i.
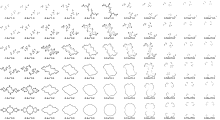
А со — серпасъясысь таблича.