Кыдзи кокньыда артавны унапельӧсалысь эрдсӧ?

Терминъяс

унапельӧса — многоугольник
эрд — площадь
мылькъя — выпуклый 
лыдмӧдны — умножить

Гаусслӧн шнуруйтан ног

Тшӧтшкӧс вылӧ гижтӧма унапельӧса. Ми тӧдам сылӧн быд йывлысь координатасӧ. Кыдзи артавны унапельӧсаыслысь эрдсӧ? Позьӧ, дерт, юклыны сійӧс куимпельӧсаяс вылӧ, быд куимпельӧсалысь артавны доръяссӧ да Герон формула отсӧгӧн эрдсӧ корсьны. Но тадзисӧ дыркодь ковмас артавны.

Вӧлӧмкӧ, эм кокньыдджык формула. Сійӧс шуӧны "Гаусслӧн шнуруйтан ногӧн".

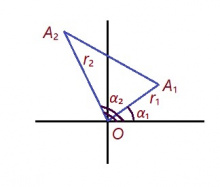
Медводз видлалам пример — OA₁A₂ куимпельӧса (сійӧс петкӧдлӧма серпас вылас); йывъясыслӧн со кутшӧм координатаяс: O = (0, 0), A₁ = (x₁, y₁), A₂ = (x₂, y₂).

Мед OA₁ вундӧглӧн кузьтаыс лоӧ r₁, а OA₂ вундӧглӧн — r₂; OA₁ да абсцисса чӧрс костын пельӧсыс лоӧ α₁, OA₂ да абсцисса чӧрс костын — α₂. Сідзкӧ

x₁ = r₁⋅cos α₁, y₁ = r₁⋅sin α₁, x₂ = r₂⋅cos α₂, y₂ = r₂⋅sin α₂,

а куимпельӧсаыслӧн эрдыс лоӧ

S = ½⋅ r₁⋅r₂⋅sin(α₂ − α₁)

= ½⋅ r₁⋅r₂⋅(sin α₂⋅cos α₁ − cos α₂⋅sin α₁)

= ½(y₂x₁ − y₁x₂).

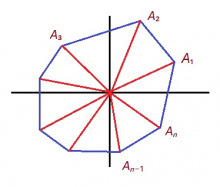
Ӧні видлалам A₁A₂...Aₙ унапельӧса; Aₖ‐лӧн координатаяс лоӧны (xₖ, yₖ); йывъяссӧ нумеруйтӧма сьӧрсьӧн-бӧрсьӧн, часі стрелка мунӧмлы паныд.

Тайӧ унапельӧсаыс кӧ мылькъя да (0, 0) чут кӧ куйлӧ сы пытшкын, ми вермам юклыны сійӧс куимпельӧсаяс вылӧ да воддза формула отсӧгӧн артавны сылысь эрдсӧ:

S = ½(y₂x₁ − y₁x₂) + ½(y₃x₂ − y₂x₃) + ... + ½(yₙxₙ₋₁ − yₙ₋₁xₙ) + ½(y₁xₙ − yₙx₁).

Вӧлӧмкӧ, кор (0, 0) чут оз куйлы унапельӧса пытшкас либӧ кор унапельӧсаыс абу мылькъя, формулаыс лоас татшӧм жӧ; бара колӧ нумеруйтны йывъяссӧ сьӧрсьӧн-бӧрсьӧн, часі стрелка мунӧмлы паныд. Медым эз ковмы тӧд вылӧ босьтны, кыдзи лыддям йывъяссӧ часі стрелка мунӧм серти, формуласӧ позьӧ гижны модульӧн:

S = ½|(y₂x₁ − y₁x₂) + ½(y₃x₂ − y₂x₃) + ... + ½(yₙxₙ₋₁ − yₙ₋₁xₙ) + ½(y₁xₙ − yₙx₁)|.

Тайӧ и эм Гаусслӧн формула. Сыӧн ёна вӧдитчӧны геодезистъяс.

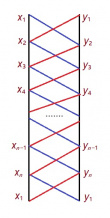
Медым формулаыс эз вун, позьӧ серпасавны татшӧм диаграмма:

Лӧз диагональяслӧн помъяс дорӧ гижӧм координатаяссӧ лыдмӧдам; сэсся гӧрд диагональяс помъяс дорӧ гижӧм координатаяссӧ лыдмӧдам да босьтам "минус" пасӧн. Сэсся став артмӧм лыдсӧ содтам. Результатсӧ юкам кык пельӧ да босьтам модуль. Диаграммаыс ботинки шнуруйтӧм кодь да, Гаусслысь формуласӧ нӧшта шуӧны "шнуруйтан ногӧн".

Содтӧд юӧр

Велӧдӧм паськӧдан блогын