Куба ӧткодьлунлӧн вужлы формула — различия между версиями
Наста (сёрнитанін | чӧжӧс) (→Италияса математикъяслӧн ног) |
Наста (сёрнитанін | чӧжӧс) (→Италияса математикъяслӧн ног) |
||
| (не показано 6 промежуточных версий этого же участника) | |||
| Строка 15: | Строка 15: | ||
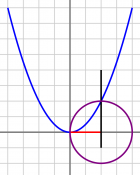
11-ӧд нэмын Омар Хайям, Персияса нималана математик да поэт, вӧзйӧма корсьны куб ӧткодьлунлысь вужсӧ геометрия ногӧн, кытшвизь да парабола отсӧгӧн. | 11-ӧд нэмын Омар Хайям, Персияса нималана математик да поэт, вӧзйӧма корсьны куб ӧткодьлунлысь вужсӧ геометрия ногӧн, кытшвизь да парабола отсӧгӧн. | ||
| + | |||
| + | [[Файл:330px-Omar Khayyam2.JPG|thumb|center|140px|]] | ||
Ӧнія терминъясӧн сылысь идеясӧ позьӧ гижны со кыдзи. Со эм ''x''³ + ''m''²''x'' − ''n'' = 0 ӧткодьлун, кӧні ''n'' > 0. Лыдмӧдам сійӧс ''x'' пӧв да гижам со кыдзи: | Ӧнія терминъясӧн сылысь идеясӧ позьӧ гижны со кыдзи. Со эм ''x''³ + ''m''²''x'' − ''n'' = 0 ӧткодьлун, кӧні ''n'' > 0. Лыдмӧдам сійӧс ''x'' пӧв да гижам со кыдзи: | ||
| Строка 21: | Строка 23: | ||
Сэсся гижтам кык чукля визь: ӧтисӧ урчитӧма ''y'' = ''x''²/''m'' ӧткодьлунӧн, мӧдсӧ урчитӧма ''y''² = ''x''(''n''/''m''² − ''x'') ӧткодьлунӧн. Медводдзаыс лоӧ парабола, мӧдыс — кытшвизь. Корсям налысь вомӧнасян чутсӧ (кодыс абу нуль); сылӧн абсциссаыс и лоас куб ӧткодьлуныслӧн вужйӧн. | Сэсся гижтам кык чукля визь: ӧтисӧ урчитӧма ''y'' = ''x''²/''m'' ӧткодьлунӧн, мӧдсӧ урчитӧма ''y''² = ''x''(''n''/''m''² − ''x'') ӧткодьлунӧн. Медводдзаыс лоӧ парабола, мӧдыс — кытшвизь. Корсям налысь вомӧнасян чутсӧ (кодыс абу нуль); сылӧн абсциссаыс и лоас куб ӧткодьлуныслӧн вужйӧн. | ||
| + | |||
| + | [[Файл:Geometric solution to cubic equation.svg.png|thumb|center|140px|]] | ||
==Италияса математикъяслӧн ног== | ==Италияса математикъяслӧн ног== | ||
| Строка 27: | Строка 31: | ||
1530-ӧд воын Никколо Тартальялы ыстасны куб ӧткодьлун кузя кык задача. Тадзи заводитчас нималана ордйысьӧм Фиор да Тарталья костын. | 1530-ӧд воын Никколо Тартальялы ыстасны куб ӧткодьлун кузя кык задача. Тадзи заводитчас нималана ордйысьӧм Фиор да Тарталья костын. | ||
| + | |||
| + | [[Файл:Tartaglia.jpg|thumb|center|140px|]] | ||
Тартальялы вӧлі вӧзйӧма ''x''³ + ''mx'' − ''n'' = 0 формаа ӧткодьлунъяслысь вуж корсьны. Сюсь математик лӧсьӧдас ӧтувъя метод да вӧзъяс Фиорлы корсьны ''x''³ + ''mx''² − ''n'' = 0 формаа ӧткодьлунлысь вужсӧ. Фиорлӧн оз артмы да ворссяс. | Тартальялы вӧлі вӧзйӧма ''x''³ + ''mx'' − ''n'' = 0 формаа ӧткодьлунъяслысь вуж корсьны. Сюсь математик лӧсьӧдас ӧтувъя метод да вӧзъяс Фиорлы корсьны ''x''³ + ''mx''² − ''n'' = 0 формаа ӧткодьлунлысь вужсӧ. Фиорлӧн оз артмы да ворссяс. | ||
1539‐ӧд воын Джероламо Кардано корас Тартальяӧс висьтавны метод йывсьыс, кӧсйысяс, ог пӧ йӧзӧд. | 1539‐ӧд воын Джероламо Кардано корас Тартальяӧс висьтавны метод йывсьыс, кӧсйысяс, ог пӧ йӧзӧд. | ||
| + | |||
| + | [[Файл:Cardano.jpg|thumb|center|140px|]] | ||
Тарталья эскас сылы да гижас вуж корсян ногсӧ кывбур формаӧн. Некымын во мысти Кардано аддзас дель Ферролысь йӧзӧдтӧм гижӧдсӧ да сюяс куба ӧткодьлун йылысь пасйӧдъяс аслас Ars Magna небӧгас. | Тарталья эскас сылы да гижас вуж корсян ногсӧ кывбур формаӧн. Некымын во мысти Кардано аддзас дель Ферролысь йӧзӧдтӧм гижӧдсӧ да сюяс куба ӧткодьлун йылысь пасйӧдъяс аслас Ars Magna небӧгас. | ||
| + | |||
| + | [[Файл:ArsMagna.jpg|thumb|center|140px|]] | ||
==Формула артмӧдӧм== | ==Формула артмӧдӧм== | ||
| Строка 38: | Строка 48: | ||
Кыдзи нӧ позьӧ артмӧдны куба ӧткодьлун вужлы формула? Гӧгӧрвоӧдам сійӧс ӧнія терминъясӧн. | Кыдзи нӧ позьӧ артмӧдны куба ӧткодьлун вужлы формула? Гӧгӧрвоӧдам сійӧс ӧнія терминъясӧн. | ||
| − | Со эм | + | Со эм ''ax''³ + ''bx''² + ''cx'' + ''d'' = 0 ӧткодьлун. Мед ''y'' = ''x'' + ''b''/3''a''. Артмас ''y''³ + ''py'' + ''q'' = 0 ӧткодьлун; ''p'' да ''q'' лыдъяссӧ позьӧ гижны ''a'', ''b'', ''c'' да ''d'' пыр — содтӧмӧн, чинтӧмӧн, лыдмӧдӧмӧн да юклӧмӧн. |
| − | Мед y = t + s. Сэки | + | Мед ''y'' = ''t'' + ''s''. Сэки |
| − | + | ''y''³ + ''py'' + ''q'' = (''t'' + ''s'')³ + ''py'' + ''q'' = ''t''³ + ''s''³ + 3''ts''(''t'' + ''s'') + ''py'' + ''q'' = | |
| − | = | + | = ''t''³ + ''s''³ + 3''tsy'' + ''py'' + ''q'' = (''t''³ + ''s''³ + ''q'') + ''y''(3''ts'' + ''p''). |
| − | Вайӧй видлам корсьны татшӧм t да s, медым | + | Вайӧй видлам корсьны татшӧм ''t'' да ''s'', медым ''t''³ + ''s''³ + ''q'' = 0 да 3''ts'' + ''p'' = 0. Вермам кӧ, ''y'' = ''t'' + ''s'' лоас ''y''³ + ''py'' + ''q'' = 0 ӧткодьлунлӧн вужйӧн. |
Сідзкӧ | Сідзкӧ | ||
| − | + | ''t''³ + ''s''³ = −''q'', ''ts'' = −''p''/3. | |
| − | Гижам кӧ u = | + | Гижам кӧ ''u'' = ''t''³, ''v'' = ''s''³, артмас: |
| − | u + v = | + | ''u'' + ''v'' = −''q'', ''uv'' = −''p''³/27, |
кытысь | кытысь | ||
| − | u( | + | ''u''(−''q'' − ''u'') = −''p''³/27. |
| − | Тайӧ квадрат ӧткодьлун, сылӧн вужйыслы вермам гижны формула. | + | Тайӧ квадрат ӧткодьлун, сылӧн вужйыслы вермам гижны формула. |
==Содтӧд юӧр== | ==Содтӧд юӧр== | ||
Текущая версия на 00:23, 10 кос му 2022
Содержание
Терминъяс
ӧткодьлун — уравнение квадрата ӧткодьлун — квадратное уравнение куба ӧткодьлун — кубическое уравнение вуж — корень лыдмӧдны — умножить
Важ история
Школаын ми велӧдлім, кыдзи гижны квадрата ӧткодьлунлысь вужсӧ формулаӧн. Тайӧ задачаыс вӧлі нин тӧдса важ Вавилонын, Египетын, Грецияын, Китайын да Индияын. Вужсӧ корсьлӧмаӧсь геометрия ногӧн (алгебра сӧвмӧдӧмаӧсь араб математикъяс, ёна сёрӧнджык).
Куба ӧткодьлунъяс паныдасьлӧны бара жӧ важ египетса, вавилонса, грецияса, китайса да индияса гижӧдъясын. Сӧмын тай уна нэм чӧжнас некодлӧн абу артмӧма лӧсьӧдны вуж корсян ногсӧ.
Омар Хайямлӧн ног
11-ӧд нэмын Омар Хайям, Персияса нималана математик да поэт, вӧзйӧма корсьны куб ӧткодьлунлысь вужсӧ геометрия ногӧн, кытшвизь да парабола отсӧгӧн.
Ӧнія терминъясӧн сылысь идеясӧ позьӧ гижны со кыдзи. Со эм x³ + m²x − n = 0 ӧткодьлун, кӧні n > 0. Лыдмӧдам сійӧс x пӧв да гижам со кыдзи:
x⁴/m² = x(n/m² − x).
Сэсся гижтам кык чукля визь: ӧтисӧ урчитӧма y = x²/m ӧткодьлунӧн, мӧдсӧ урчитӧма y² = x(n/m² − x) ӧткодьлунӧн. Медводдзаыс лоӧ парабола, мӧдыс — кытшвизь. Корсям налысь вомӧнасян чутсӧ (кодыс абу нуль); сылӧн абсциссаыс и лоас куб ӧткодьлуныслӧн вужйӧн.
Италияса математикъяслӧн ног
16-ӧд нэм заводитчигӧн италияса математик Сципионе дель Ферро гӧгӧрвоас, кыдзи корсьны x³ + mx − n = 0 ӧткодьлунлысь вужсӧ, но оз йӧзӧд ассьыс мӧвпъяссӧ. Сӧмын кулӧм водзас сійӧ юксяс тайӧ гусяторнас аслас велӧдчысьыскӧд, Антонио Фиоркӧд.
1530-ӧд воын Никколо Тартальялы ыстасны куб ӧткодьлун кузя кык задача. Тадзи заводитчас нималана ордйысьӧм Фиор да Тарталья костын.
Тартальялы вӧлі вӧзйӧма x³ + mx − n = 0 формаа ӧткодьлунъяслысь вуж корсьны. Сюсь математик лӧсьӧдас ӧтувъя метод да вӧзъяс Фиорлы корсьны x³ + mx² − n = 0 формаа ӧткодьлунлысь вужсӧ. Фиорлӧн оз артмы да ворссяс.
1539‐ӧд воын Джероламо Кардано корас Тартальяӧс висьтавны метод йывсьыс, кӧсйысяс, ог пӧ йӧзӧд.
Тарталья эскас сылы да гижас вуж корсян ногсӧ кывбур формаӧн. Некымын во мысти Кардано аддзас дель Ферролысь йӧзӧдтӧм гижӧдсӧ да сюяс куба ӧткодьлун йылысь пасйӧдъяс аслас Ars Magna небӧгас.
Формула артмӧдӧм
Кыдзи нӧ позьӧ артмӧдны куба ӧткодьлун вужлы формула? Гӧгӧрвоӧдам сійӧс ӧнія терминъясӧн.
Со эм ax³ + bx² + cx + d = 0 ӧткодьлун. Мед y = x + b/3a. Артмас y³ + py + q = 0 ӧткодьлун; p да q лыдъяссӧ позьӧ гижны a, b, c да d пыр — содтӧмӧн, чинтӧмӧн, лыдмӧдӧмӧн да юклӧмӧн.
Мед y = t + s. Сэки
y³ + py + q = (t + s)³ + py + q = t³ + s³ + 3ts(t + s) + py + q =
= t³ + s³ + 3tsy + py + q = (t³ + s³ + q) + y(3ts + p).
Вайӧй видлам корсьны татшӧм t да s, медым t³ + s³ + q = 0 да 3ts + p = 0. Вермам кӧ, y = t + s лоас y³ + py + q = 0 ӧткодьлунлӧн вужйӧн.
Сідзкӧ
t³ + s³ = −q, ts = −p/3.
Гижам кӧ u = t³, v = s³, артмас:
u + v = −q, uv = −p³/27,
кытысь
u(−q − u) = −p³/27.
Тайӧ квадрат ӧткодьлун, сылӧн вужйыслы вермам гижны формула.