Кыдзи ыдждӧдны куб кык пӧв — различия между версиями

Материал из Коми тӧданін
(→‎Кыдзи нӧ позьӧ кубсӧ кык пӧв ыдждӧны?)
(→‎Кыдзи нӧ позьӧ кубсӧ кык пӧв ыдждӧны?)
Строка 16: Строка 16:
 
==Кыдзи нӧ позьӧ кубсӧ кык пӧв ыдждӧны?==
 
==Кыдзи нӧ позьӧ кубсӧ кык пӧв ыдждӧны?==
  
−
Кублӧн кӧ дорыс a кузьта, сылӧн йӧрышыс лоӧ a<sup>3</sup>. Колӧ артмӧдны 2a<sup>3</sup> йӧрыша куб. Сылӧн дорыс <sup>3</sup>√2a ыджда. Сідзкӧ, сетӧма кӧ a кузьта вундӧг, колӧ артмӧдны <sup>3</sup>√2a кузьта вундӧгсӧ.
+
Кублӧн кӧ дорыс a кузьта, сылӧн йӧрышыс лоӧ ''a''<sup>3</sup>. Колӧ артмӧдны 2''a''<sup>3</sup> йӧрыша куб. Сылӧн дорыс <sup>3</sup>√2''a'' ыджда. Сідзкӧ, сетӧма кӧ a кузьта вундӧг, колӧ артмӧдны <sup>3</sup>√2''a'' кузьта вундӧгсӧ.
  
 
[[Файл:Cube and doubled cube.png|thumb|center|330px|]]
 
[[Файл:Cube and doubled cube.png|thumb|center|330px|]]
Строка 24: Строка 24:
 
А со кутшӧм ногӧн вундӧгсӧ <sup>3</sup>√2 пӧв ыдждӧдлӧма Исаак Ньютон. Мед сетӧма a кузьта вундӧг.
 
А со кутшӧм ногӧн вундӧгсӧ <sup>3</sup>√2 пӧв ыдждӧдлӧма Исаак Ньютон. Мед сетӧма a кузьта вундӧг.
  
−
1. Линейка вылас G, H чутъяс пасъям сідзи, медым GH = a.
+
1. Линейка вылас ''G'', ''H'' чутъяс пасъям сідзи, медым ''GH'' = ''a''.
−
2. Артмӧдам a кузьта доръяса ABC куимпельӧса.
+
 
−
3. Нюжӧдам AB да BC вундӧгъяссӧ веськыд визьясӧдз.
+
2. Артмӧдам ''a'' кузьта доръяса ''ABC'' куимпельӧса.
−
4. AB веськыд визь вылӧ пуктам D чутсӧ сідз, медым B куйліс A да D костын, AB = BD.
+
 
−
5. D да C чутъяс пыр веськыд визь нуӧдам.
+
3. Нюжӧдам ''AB'' да ''BC'' вундӧгъяссӧ веськыд визьясӧдз.
−
6. Линейкасӧ пуктам сідз, медым сійӧ муніс A чут пыр, H чут куйліс BC визьньӧв вылын, а G куйліс A да H костын, DC визьньӧв вылын.
+
 
 +
4. ''AB'' веськыд визь вылӧ пуктам ''D'' чутсӧ сідз, медым ''B'' куйліс ''A'' да ''D'' костын, ''AB'' = ''BD''.
 +
 
 +
5. ''D'' да ''C'' чутъяс пыр веськыд визь нуӧдам.
 +
6. Линейкасӧ пуктам сідз, медым сійӧ муніс ''A'' чут пыр, ''H'' чут куйліс ''BC'' визьньӧв вылын, а ''G'' куйліс ''A'' да ''H'' костын, ''DC'' визьньӧв вылын.
  
 
[[Файл:Doubling the cube.png|thumb|center|330px|]]
 
[[Файл:Doubling the cube.png|thumb|center|330px|]]
  
−
Вӧлӧмкӧ, AG = <sup>3</sup>√2.
+
Вӧлӧмкӧ, ''AG'' = <sup>3</sup>√2''a''.
  
 
===Подулалӧм===
 
===Подулалӧм===
  
−
Математика тӧдысьяслы инда, кыдзи, тайӧс аддзыны. Шуам, a = 1. Мед AG = x, HC = z. Менелай теорема серти,  
+
Математика тӧдысьяслы инда, кыдзи, тайӧс аддзыны. Шуам, ''a'' = 1. Мед ''AG'' = ''x'', ''HC'' = ''z''. Менелай теорема серти,  
−
(AG : GH)∙(HC : BC)∙(BD : DA) = 1,  
+
 
−
кытысь артмас xz = 2. Сэсся ABH куимпельӧсалы косинусъяс йылысь теоремасӧ гижам. Артмӧдам: x2 + 2x = z2 + z. Сідзкӧ, z4 + z3 – 4z – 4 = 0, кытысь z = –1 либӧ z = <sup>3</sup>√4. Минуса лыд миянлы оз лӧсяв. Та вӧсна z = <sup>3</sup>√4, x = <sup>3</sup>√2.
+
(''AG'' : ''GH'')∙(''HC'' : ''BC'')∙(''BD'' : ''DA'') = 1,  
 +
 
 +
кытысь артмас ''xz'' = 2. Сэсся ''ABH'' куимпельӧсалы косинусъяс йылысь теоремасӧ гижам. Артмӧдам: ''x''<sup>2</sup> + 2''x'' = ''z''<sup>2</sup> + ''z''. Сідзкӧ, ''z''<sup>4</sup> + ''z''<sup>3</sup> – 4''z'' – 4 = 0, кытысь ''z'' = –1 либӧ ''z'' = <sup>3</sup>√4. Минуса лыд миянлы оз лӧсяв. Та вӧсна ''z'' = <sup>3</sup>√4, ''x'' = <sup>3</sup>√2.
  
 
==Пасйӧд==
 
==Пасйӧд==

Версия 00:42, 23 кӧч 2020

Терминъяс

йӧрыш – объём
вундӧг – отрезок
куимпельӧса – треугольник
визьньӧв – луч

Важ легенда

Тайӧ мог йылысь со кутшӧм легенда кольӧма. Чума дырйи Афиныын олысьяс юалӧмаӧсь Дельфыса оракуллысь, кыдзи мынны тайӧ приччаысь. Ен тшӧктӧма налы алтарсӧ кык пӧв ыдждӧдны да вись (жертва) вайны. Алтарыс вӧлі куб кодь да, афинысаяс лӧсьӧдӧмаӧсь сэтшӧм жӧ кубсӧ да пуктӧмаӧсь алтар вылас. Сӧмын пӧрӧсыс эз быр. Сэсся найӧ Платон дорӧ шыӧдчӧмаӧсь. Сійӧ шуӧма, Ен пӧ скӧрмӧ тіян вылӧ геометрия тӧдтӧмлунсьыныд, колӧ пӧ вӧчны куб мыгӧра алтарсӧ. Афинысаяс тайӧс вӧчӧмаӧсь да сӧмын сы бӧрын чумаыд бырӧма.

Platon.jpg

Збыльысь кӧ, тайӧ мог йывсьыс водзджык тӧдӧмаӧсь — сы йылысь Хиосса Гиппократ на мӧвпалӧма.

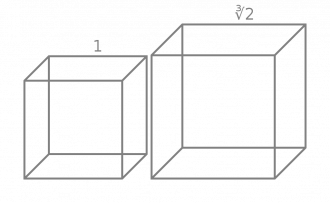
Кыдзи нӧ позьӧ кубсӧ кык пӧв ыдждӧны?

Кублӧн кӧ дорыс a кузьта, сылӧн йӧрышыс лоӧ a3. Колӧ артмӧдны 2a3 йӧрыша куб. Сылӧн дорыс 3√2a ыджда. Сідзкӧ, сетӧма кӧ a кузьта вундӧг, колӧ артмӧдны 3√2a кузьта вундӧгсӧ.

Cube and doubled cube.png

Позьӧ-ӧ татшӧм вундӧгсӧ циркульӧн да линейкаӧн артмӧдны? Вӧлӧмкӧ, оз. Тайӧс 1837-ӧд воын петкӧдлӧма Пьер Ванцель. (Ми гаравлім нин сылысь нимсӧ пельӧс трисектриса йылысь гижигӧн.)

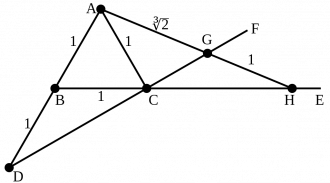
А со кутшӧм ногӧн вундӧгсӧ 3√2 пӧв ыдждӧдлӧма Исаак Ньютон. Мед сетӧма a кузьта вундӧг.

1. Линейка вылас G, H чутъяс пасъям сідзи, медым GH = a.

2. Артмӧдам a кузьта доръяса ABC куимпельӧса.

3. Нюжӧдам AB да BC вундӧгъяссӧ веськыд визьясӧдз.

4. AB веськыд визь вылӧ пуктам D чутсӧ сідз, медым B куйліс A да D костын, AB = BD.

5. D да C чутъяс пыр веськыд визь нуӧдам. 6. Линейкасӧ пуктам сідз, медым сійӧ муніс A чут пыр, H чут куйліс BC визьньӧв вылын, а G куйліс A да H костын, DC визьньӧв вылын.

Doubling the cube.png

Вӧлӧмкӧ, AG = 3√2a.

Подулалӧм

Математика тӧдысьяслы инда, кыдзи, тайӧс аддзыны. Шуам, a = 1. Мед AG = x, HC = z. Менелай теорема серти, 

(AG : GH)∙(HC : BC)∙(BD : DA) = 1,

кытысь артмас xz = 2. Сэсся ABH куимпельӧсалы косинусъяс йылысь теоремасӧ гижам. Артмӧдам: x2 + 2x = z2 + z. Сідзкӧ, z4 + z3 – 4z – 4 = 0, кытысь z = –1 либӧ z = 3√4. Минуса лыд миянлы оз лӧсяв. Та вӧсна z = 3√4, x = 3√2.

Пасйӧд

Содтӧд юӧр

Велӧдӧм паськӧдан блогын.

Источник — «http://wiki.komikyv.org/index.php?title=Кыдзи_ыдждӧдны_куб_кык_пӧв&oldid=74365»