Планиметрия курс — различия между версиями
Наста (сёрнитанін | чӧжӧс) (→Ӧтнырвизя (параллель) веськыдъяс) |
Наста (сёрнитанін | чӧжӧс) (→Параллель веськыдъяс торъяланлунъяс) |
||
| Строка 463: | Строка 463: | ||
===Параллель веськыдъяс торъяланлунъяс=== | ===Параллель веськыдъяс торъяланлунъяс=== | ||
| + | |||
| + | '''Теорема.''' Сетӧма кык ӧтнырвизя веськыд да найӧс вундысь. Сэки артмӧм пытшкӧсса падвежӧнкуйлысь пельӧсъяс ӧтыдждаӧсь. | ||
| + | |||
| + | '''Эскӧдӧм.''' Мед ∠''DAB'' да ∠''CBA'' абу ӧтыдждаӧсь. Нуӧдам ''A'' чут пыр ''AE'' веськыдӧс сідзи, медым ∠''EAB'' = ∠''CBA''. Сідзкӧ, ''EA'' да ''BC'' веськыдъяс ӧтнырвизяӧсь. Та вӧсна ''A'' чут пыр мунӧ ''BC''-кӧд ӧтнырвизя кык веськыд: ''AD'' да ''AE''. Тайӧ кыв вожалӧм. | ||
| + | |||
| + | '''Кывкӧртӧд.''' Сетӧма кык ӧтнырвизя веськыд да найӧс вундысь. Сэки | ||
| + | 1) артмӧм ортсыса падвежӧнкуйлысь пельӧсъяс ӧтыдждаӧсь; | ||
| + | 2) артмӧм весьтаса пельӧсъяс ӧтыдждаӧсь; | ||
| + | 3) артмӧм пытшкӧсса ӧтарбокса пельӧсъяс содтасыс 180° ыджда; | ||
| + | 4) артмӧм ортсыса ӧтарбокса пельӧсъяс содтасыс 180° ыджда. | ||
==Содтӧд юӧр== | ==Содтӧд юӧр== | ||
[[Category:Математика школаын]] | [[Category:Математика школаын]] | ||
Версия 00:48, 12 вӧльгым 2020
Содержание
- 1 Веськыд визь йылысь
- 2 Пельӧс йылысь
- 3 Куимпельӧсаяс
- 3.1 Куимпельӧсаяс ӧткодьлун йылысь медводдза тӧдмӧс
- 3.2 Ӧткодь берда да ӧткодь доръяса куимпельӧсаяс
- 3.3 Куимпельӧсаяс ӧткодьлун йылысь мӧд тӧдмӧс
- 3.4 Биссектриса, медиана да судта
- 3.5 Куимпельӧсаяс ӧткодьлун йылысь коймӧд тӧдмӧс
- 3.6 Веськыд визьысь ортсыын куйлысь чут пыр гижтӧм ӧшанвизь
- 3.7 Ортсыса пельӧс
- 3.8 Куимпельӧса доръяс да пельӧсъяс ӧтластитӧм
- 3.9 Куимпельӧса ӧткодьтӧмлун
- 4 Ӧтнырвизя (параллель) веськыдъяс
- 5 Содтӧд юӧр
Веськыд визь йылысь
тшӧтшкӧс – плоскость веськыд визь – прямая чут – точка мыгӧр – фигура кывкӧртӧд – следствие эскӧдӧм – доказательство кыв вожалӧм – противоречие
Планиметрияӧн шусьӧ геометриялӧн юкӧн, кӧні велӧдӧны тшӧтшкӧсвывса мыгӧръяс.
Тшӧтшкӧслысь, веськыд визьлысь, чутлысь медшӧр торъяланлунъяссӧ индам аксиомаяс пыр.
Аксиома. Эм кӧ тшӧтшкӧсын веськыд визь, сэк тшӧтшкӧсса чутъяс пӧвстысь кодсюрӧяс лоасны тайӧ визьын, а мукӧдыс сыысь ортсын.
Аксиома. Кык торъялана чут пыр позьӧ нуӧдны веськыд визь; татшӧм визьыс овлӧ сӧмын ӧти.
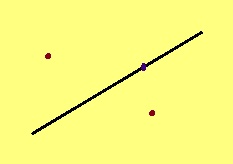
Кывкӧртӧд. Вомӧнасьӧны кӧ кык торъялана веськыд визь, вомӧнасян чутныс лоӧ сӧмын ӧти.
Эскӧдӧм. Мед, шуам, веськыд визьясыс вомӧнасьӧны торъялана кык чутын. Сідзкӧ, тайӧ чутъяс пырыс позьӧ гижтыны кык торъялана веськыд визь. А аксиомаыд серти, татшӧм визьыс на пыр вермас мунны сӧмын ӧти. Артмӧ кыв вожалӧм.
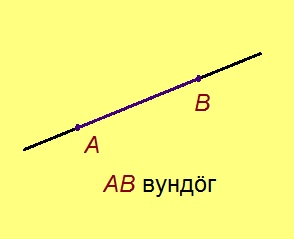
Вундӧг
вундӧг – отрезок
Аксиома. Ӧти веськыд визьса куим торъялан чут пиысь ӧтиыс лоӧ мӧд кык костас; татшӧм чутыс овлӧ сӧмын ӧти.
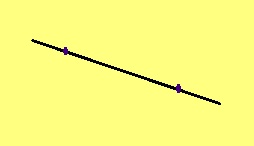
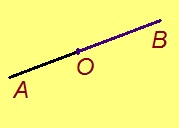
Кык чут на костса став чутыскӧд ӧтув артмӧдӧны вундӧг. Индӧм кык чутыс шусьӧны вундӧг помъясӧн.
Аксиома. Быд вундӧглӧн эм кузьта – плюса лыд.
Вундӧг помъясын кӧ А да В чутъяс, шуам татшӧм вундӧгсӧ АВ; тадзи жӧ и сылысь кузьтасӧ шуам.
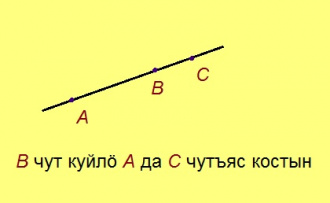
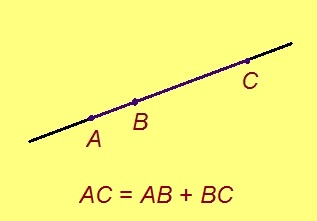
Аксиома. Мед ӧти веськыд визьын эм куим торъя чут: A, B да C; B-ыс куйлӧ A да C костас. Сэки AC = AB + BC.
Кывкӧртӧд. Мед ӧти веськыд визьын эм куим торъя чут: A, B да C; B-ыс куйлӧ A да C костас. Сэки AC > AB, AC > BC.
Кывкӧртӧд. Мед ӧти веськыд визьын эм куим торъя чут: A, B да C; AC = AB + BC. Сэки B-ыс куйлӧ A да C костас.
Эскӧдӧм. Миян артмӧ: AC > AB, AC > BC. A чутыс кӧ куйлӧ B да C костас, BC > AC; C чутыс кӧ куйлӧ A да B костас, AB > AC. Сідзкӧ, B-ыс куйлӧ A да C костас.
Тшӧтшкӧсджын
тшӧтшкӧсджын – полуплоскость
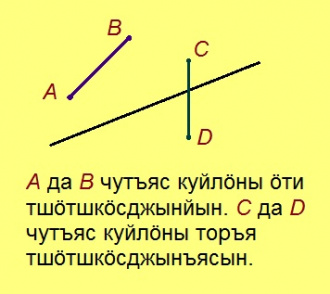
Аксиома. Быд веськыд визь юклӧ тшӧтшкӧссӧ кык тшӧтшкӧсджын вылӧ. Кык чут A да B куйлӧны ӧти тшӧтшкӧсджынйын, оз кӧ AB вундӧгыс вомӧнав индӧм веськыд визьсӧ.
Сідзкӧ, AB-ыс кӧ вомӧналӧ тайӧ веськыд визьсӧ, A да B чутъясыс куйлӧны торъя тшӧтшкӧсджынъясын.
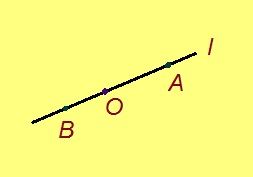
Аксиома. Сетӧма кӧ l веськыд визь да сы вылын куйлысь O чут, быть сюрасны и сэтшӧм A да B чутъяс, кодъяслы лӧсялӧ татшӧмтор: A, O, B абу ӧтилаынӧсь, A да B куйлӧны l вылын да O чутыс куйлӧ A да B чутъяс костын.
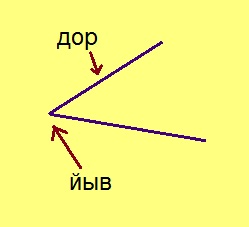
Визьньӧв
визьньӧв – луч веськыд визьджын – полупрямая
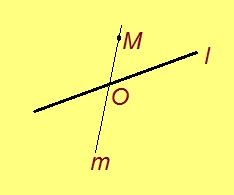
Мед O чут куйлӧ l веськыд визь вылын. Босьтам l сайын куйлысь M чутсӧ. Нуӧдам O да M чутъяс пыр m веськыд визьсӧ. Сэки m юклӧ тшӧтшкӧссӧ кык тшӧтшкӧсджын вылӧ.
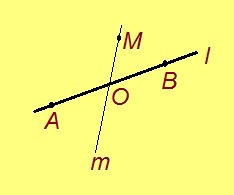
Мед A да B чутъяс куйлӧны l веськыд визь вылын. Аксиома серти, найӧ куйлӧны торъя тшӧтшкӧсджынъясын сэк да сӧмын сэк, кор O чут куйлӧ AB вундӧгын. Сідзкӧ, O чут юклӧ l веськыдсӧ кык юкӧн вылӧ; тайӧ юкӧнъясыс шусьӧны визьньӧвъясӧн либӧ веськыд визьджынъясӧн.
OA да OB – кык визьньӧв:
Аксиома. Быд визьньӧвйӧ сы йывсяньыс сетӧм кузьтаӧн позьӧ гижтыны дзик ӧти вундӧг.
Пельӧс йылысь
пельӧс – угол пельӧс дор – сторона угла пельӧс йыв – вершина угла павтыртӧм пельӧс – развёрнутый угол ёсь пельӧс – острый угол веськыд пельӧс – прямой угол тшӧтшыд пельӧс – тупой угол орчча пельӧсъяс – смежные углы вертикаль пельӧсъяс – вертикальные углы
Ӧти чутысь петысь кык визьньӧв артмӧдӧны пельӧс. Тайӧ визьньӧвъясыс шусьӧны пельӧс доръясӧн, а налӧн ӧтувъя чутыс – пельӧс йылӧн.
Пельӧс доръяс костса визьньӧв
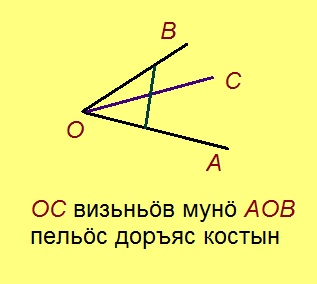
Урчитӧм. Визьньӧв мунӧ пельӧс доръяс костӧд, сылӧн помыс кӧ лӧсялӧ пельӧс йывкӧд да сійӧ кӧ вомӧнасьӧ кутшӧмкӧ вундӧгкӧд, кодлӧн помъясыс куйлӧны пельӧс доръяс вылас.
Висьталӧм. Визьньӧв кӧ мунӧ пельӧс доръяс костӧд, сійӧ вомӧнасьӧ быд вундӧгкӧд, кодлӧн помъясыс куйлӧны пельӧс доръяс вылас.
Эскӧдӧм. Мед O – кутшӧмкӧ пельӧслӧн йыв, OM – визьньӧв, коді мунӧ пельӧс доръяс костӧд. Урчитӧм серти, OM вомӧнасьӧ кутшӧмкӧ AB вундӧгкӧд, кӧні A да B чутъясыс куйлӧны пельӧс доръяс вылас. Мед CD – мӧд вундӧг, C куйлӧ OA визьньӧв вылын, D куйлӧ OB визьньӧв вылын.
OM веськыд визь юкӧ тшӧтшкӧссӧ кык тшӧтшкӧсджынйӧ; аксиома серти, A да B чутъяс оз ӧти тшӧтшкӧсджынас куйлыны. A да C чутъяс куйлӧны OA визьньӧв вылын, та вӧсна найӧ куйлӧны ӧти тшӧтшкӧсджынйын, OM веськыд визь серти кӧ. Сідзи жӧ артмӧ: B да D чутъяс куйлӧны ӧти тшӧтшкӧсджынйын, OM веськыд визь серти жӧ. Сідзкӧ, CD вундӧг вомӧнасьӧ OM веськыд визьыскӧд. Пасъям вомӧнасян чутсӧ N шыпасӧн.
Петкӧдлам, мый "ОМ" веськыд визьвывса N чут куйлӧ ОМ визьньӧв вылын. N кӧ тайӧ визьньӧв вылас эз куйлы, O чут куйліс эськӧ M да N костын. Сэки, босьтам кӧ тшӧтшкӧссӧ кык джынйӧ юкысь пыдди OB веськыд визь, M да N эз эськӧ куйлыны ӧти тшӧтшкӧсджынас. Но CA, CN, AM вундӧгъяс оз вомӧнасьны OB веськыд визьыскӧд. Сідзкӧ, OB веськыд визь серти кӧ, N, C, A, М чутъяс куйлӧны ӧти тшӧтшкӧсджынйын. Артмис кыв вожалӧм.
Пельӧс градуса муртӧс
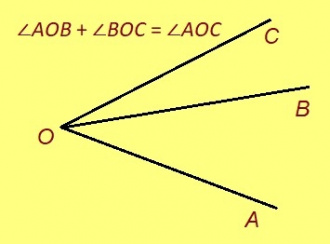
Урчитӧм. Пельӧслӧн доръясыс кӧ артмӧдӧны веськыд визь, сійӧ шусьӧ павтыртӧм пельӧсӧн. Аксиомаяс. 1. Быд пельӧс позьӧ муртавны плюса градусӧн. 2. Визьньӧв кӧ мунӧ пельӧс доръяс костӧд, сэки тайӧ пельӧсас сымда жӧ градус, мыйта визьньӧвнас артмӧдӧм кыкнан пельӧсас ӧтув босьтӧмӧн.
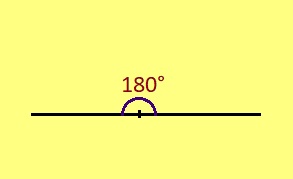
3. Павтыртӧм пельӧсыс лоӧ 180° ыджда.
4. Быд визьньӧвсянь позьӧ бӧрйӧм тшӧтшкӧсджынйӧ пуктыны сетӧм муртӧсӧн дзик ӧти пельӧс (медтыкӧ 180°-ысь ыджыдджык эз вӧв-а).
Орчча пельӧсъяс
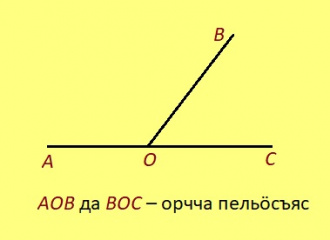
Урчитӧм. Кык пельӧс шусьӧ орччаӧн, налӧн кӧ эм ӧтувъя дор, а мӧд доръяс кӧ артмӧдӧны веськыд визь.
Теорема. Ӧтувтам кӧ орчча пельӧсъяслысь ыджданысӧ, лоӧ 180°. Эскӧдӧм. Орчча пельӧсъяс артмӧдӧны павтыртӧм пельӧссӧ, кодлӧн ыдждаыс 180°. Сідзкӧ, 2-ӧд аксиома серти, налӧн суммаыс лоас 180°. Кывкӧртӧд. Пельӧсыс кӧ 90° ыджда, сыкӧд орчча пельӧсыс сідзжӧ 90° ыджда.
Веськыд, ёсь да тшӧтшыд пельӧсъяс
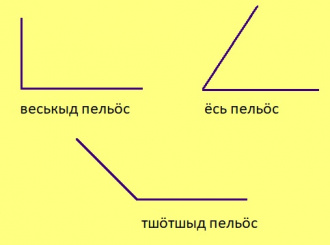
Урчитӧм. Пельӧс шусьӧ ёсьӧн, сылӧн градуса муртӧсыс кӧ 90°-ысь этшаджык; веськыдӧн, сійӧ кӧ 90° ыджда; тшӧтшыдӧн, сійӧ кӧ 90°-ысь ыджыдджык.
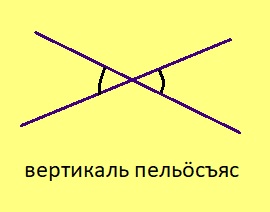
Вертикаль пельӧсъяс
Урчитӧм. Кык пельӧс шусьӧ вертикаль пельӧсъясӧн, ӧтиыслӧн доръясыс кӧ лоӧны мӧд пельӧсса доръяслӧн нюжӧдӧмӧн.
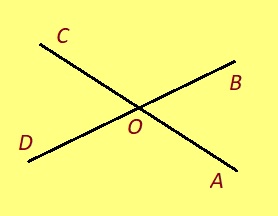
Теорема. Вертикаль пельӧсъяс ӧтыдждаӧсь. Эскӧдӧм. Серпас серти, ∠AOB да ∠BOC орччаӧсь, ∠BOC да ∠COD орччаӧсь. Та вӧсна ∠AOB + ∠BOC = 180°, ∠BOC + ∠COD = 180°. Сідзкӧ, ∠AOB = 180° – ∠BOC = ∠COD.
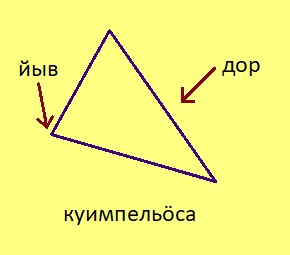
Куимпельӧсаяс
куимпельӧса – треугольник ӧткодь куимпельӧсаяс – равные треугольники
Урчитӧм. Куимпельӧсаӧн шусьӧ куим чутысь (кодъяс оз куйлыны ӧти веськыд визь вылын) да найӧс йитан вундӧгъясысь тэчӧм мыгӧр. Чутъясыс шусьӧны куимпельӧса йывъясӧн, вундӧгъясыс шусьӧны куимпельӧса доръясӧн.
A йывбердса пельӧсӧн ABC куимпельӧсаын шусьӧ AB да AС визьньӧвъясӧн артмӧм пельӧс.
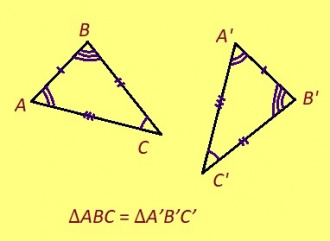
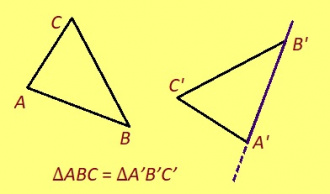
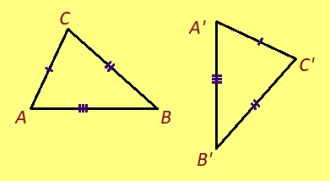
Урчитӧм. ABC да A’B’C’ куимпельӧсаяс ӧткодьӧсь, налӧн кӧ ӧта-мӧдыслы лӧсялана пельӧсъяс ӧтыдждаӧсь да ӧта-мӧдыслы лӧсялана доръясыс ӧтыдждаӧсь: ∠A = ∠A’, ∠B = ∠B’, ∠C = ∠C’, AB = A’B’, AC = A’C’, BC = B’C’.
Сетӧма визьньӧв. Сылӧн нюжӧдӧмыс – веськыд визь; сійӧ юклӧ тшӧтшкӧссӧ кык тшӧтшкӧсджын вылӧ. Бӧръям на пиысь ӧтиӧс. Мед нӧшта сетӧма ABC куимпельӧса.
Аксиома. Индӧм тшӧтшкӧсджынйӧ позьӧ пуктыны ABC-кӧд ӧткодь A’B’C’ куимпельӧса сідзи, медым A’B’ вундӧг куйліс индӧм визьньӧвйын да A’ ӧтлаасис сылӧн воддза чуткӧд.
Куимпельӧсаяс ӧткодьлун йылысь медводдза тӧдмӧс
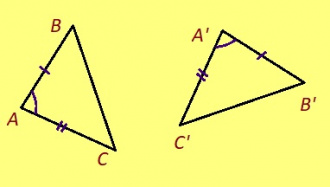
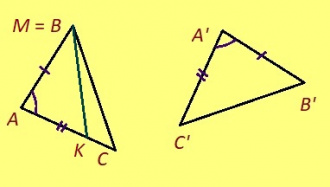
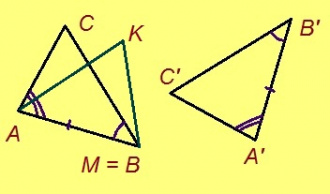
Теорема. Мед ABC да A’B’C’ – куимпельӧсаяс, AB = A’B’, AC = A’C’, ∠A = ∠A’. Сэки ∆ABC = ∆A’B’C’.
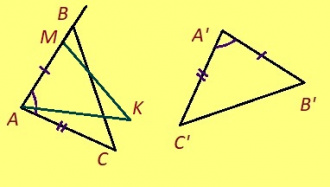
Эскӧдӧм. Аксиомаысь петӧ: эм сэтшӧм торъяланлуна AMK куимпельӧса: 1) ∆AMK = ∆A’B’C’, 2) AM куйлӧ AB визьньӧв пытшкын, 3) AMK да ABC куйлӧны ӧти тшӧтшкӧсджынйын AB веськыд визь серти.
∆AMK = ∆A’B’C’, та вӧсна AM = A’B’, AK = A’C’, ∠B’A’C’ = ∠MAK. Сідзкӧ:
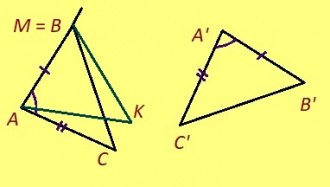
1) AB = A’B’ = AM да, M = B;
2) ∠BAC = ∠B’A’C’ = ∠BAK, та вӧсна AK да AC визьньӧвъяс лӧсялӧны;
3) AC = A’C’ = AK да, K = C.
Кык чут пыр мунӧ сӧмын ӧти веськыд визь. Сідзкӧ, AMK да ABC куимпельӧсаяс лӧсялӧны. Та вӧсна ∆ABC = ∆A’B’C’.
Ӧткодь берда да ӧткодь доръяса куимпельӧсаяс
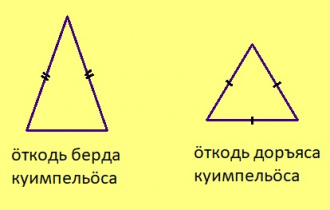
ӧткодь берда куимпельӧса – равнобедренный треугольник ӧткодь доръяса куимпельӧса – равносторонний треугольник боквыв доръяс – боковые стороны подув – основание
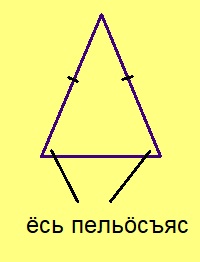
Урчитӧм. Куимпельӧса шусьӧ ӧткодь бердаӧн, сылӧн кӧ эм кык ӧтыджда дор. Куимпельӧса шусьӧ ӧткодь доръясаӧн, сылӧн кӧ куимнан дорыс ӧтыджда.
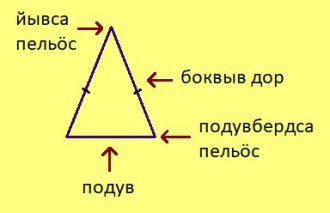
Ӧткодь берда куимпельӧсаын ӧткодь доръясыс шусьӧны боквыв доръясӧн, коймӧд дорыс шусьӧ подулӧн. Подувлы паныд куйлысь пельӧс шусьӧ йывса пельӧсӧн, боквыв дорлы паныд куйлысь пельӧс шусьӧ подувбердса пельӧсӧн.
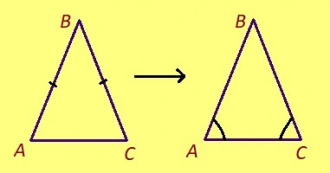
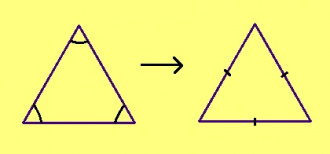
Теорема. Ӧткодь берда куимпельӧсаын подувбердса пельӧсъяс ӧтыдждаӧсь.
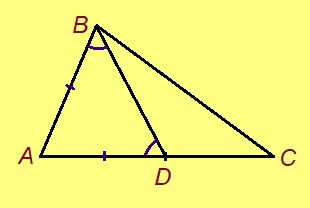
Эскӧдӧм. Мед ABC – ӧткодь берда куимпельӧса, AB = BC. Лыддям куимпельӧсаыслысь йывъяссӧ торъя ногӧн: ABC да CBA. Артмӧдам кык торъя куимпельӧса. ∆ABC = ∆CBA медводдза тӧдмӧс серти: AB = BC, CB = BA, на костса B пельӧс ӧтувъя. Сідзкӧ, ∠BAC = ∠BCA.
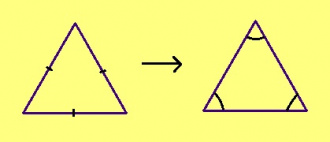
Кывкӧртӧд. Ӧткодь доръяса куимпельӧсалӧн куимнан пельӧсыс ӧтыджда.
Куимпельӧсаяс ӧткодьлун йылысь мӧд тӧдмӧс
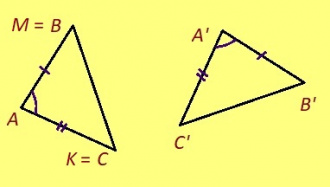
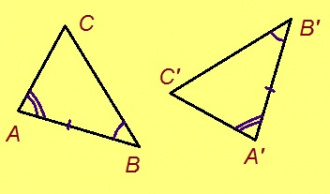
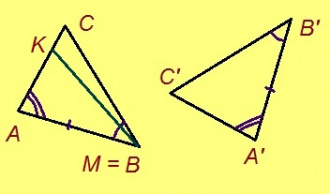
Теорема. Мед ABC да A’B’C’ – куимпельӧсаяс, AB = A’B’, ∠A = ∠A’, ∠B = ∠B’. Сэки ∆ABC = ∆A’B’C’.
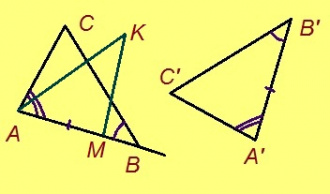
Эскӧдӧм. Аксиомаысь петӧ: эм сэтшӧм торъяланлуна AMK куимпельӧса: 1) ∆AMK = ∆A’B’C’, 2) AM куйлӧ AB визьньӧв пытшкын, 3) AMK да ABC куйлӧны ӧти тшӧтшкӧсджынйын AB веськыд визь серти.
∆AMK = ∆A’B’C’, та вӧсна AM = A’B’, ∠B’A’C’ = ∠MAK, ∠A’B’C’ = ∠AMK. Сідзкӧ:
1) AB = A’B’ = AM да, M = B;
2) ∠BAC = ∠B’A’C’ = ∠BAK, та вӧсна AK да AC визьньӧвъяс лӧсялӧны;
3) ∠ABC = ∠A’B’C’ = ∠ABK, та вӧсна BK да BC визьньӧвъяс лӧсялӧны.
Кык торъялана веськыд визь вомӧнасьӧны сӧмын ӧти чутын. Сідзкӧ, K = C. Та вӧсна AMK да ABC куимпельӧсаяс лӧсялӧны да ∆ABC = ∆A’B’C’.
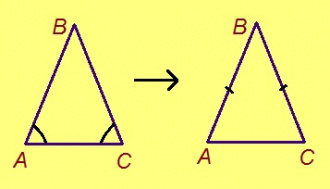
Теорема. Куимпельӧсаын кӧ эм кык ӧтыджда пельӧсыс, сійӧ ӧткодь берда.
Эскӧдӧм. Мед ABC – куимпельӧса, ∠A = ∠C. Лыддям куимпельӧсаыслысь йывъяссӧ торъя ногӧн: ABC да CBA. ∆ABC = ∆CBA мӧд тӧдмӧс серти: AB дорыс налӧн ӧтувъя, ∠A = ∠C, ∠C = ∠A. Сідзкӧ, AB = BC.
Кывкӧртӧд. Куимпельӧса ӧткодь берда сэк да сӧмын сэк, кор сылӧн эм кык ӧтыжда пельӧс.
Кывкӧртӧд. Куимпельӧса ӧткодь доръяса сэк да сӧмын сэк, кор сылӧн куимнан пельӧсыс ӧтыдждаӧсь.
Биссектриса, медиана да судта
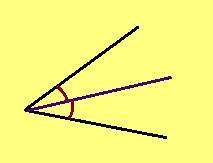
Урчитӧм. Пельӧс биссектрисаӧн шусьӧ сылӧн йылысь петысь визьньӧв, коді юклӧ тайӧ пельӧссӧ шӧрипӧв.
Урчитӧм. Куимпельӧсаса индӧм йылысь гижтӧм биссектрисаӧн шусьӧ тайӧ йыла пельӧс биссектрисаса вундӧг, коді йитӧ йывсӧ да сылы паныда куйлысь дорвывса чутсӧ.
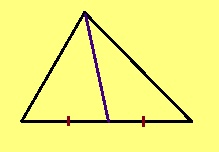
Урчитӧм. Куимпельӧсаса индӧм йылысь гижтӧм медианаӧн шусьӧ тайӧ йывсӧ паныда дорса шӧркӧд йитысь вундӧг.
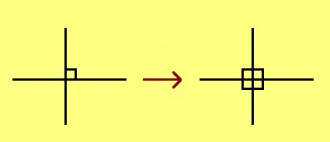
Мед кык веськыд визь вомӧнасьӧны да ӧти артмӧм пельӧс веськыд. Сэки сыкӧд орчча пельӧсъясыс веськыдӧсь да сылы вертикаль пельӧсыс веськыд.
Урчитӧм. Веськыд визь шусьӧ ӧшанвизьӧн мӧд веськыд визьлы, найӧ кӧ артмӧдӧны веськыд пельӧс.
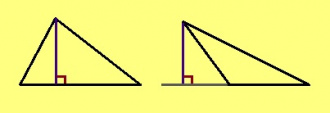
Урчитӧм. Куимпельӧсаса индӧм йылысь петысь судтаӧн шусьӧ тайӧ йывсянь паныда дорсӧ кутысь веськыд визьӧ гижтӧм ӧшанвизь.
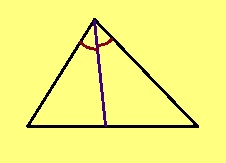
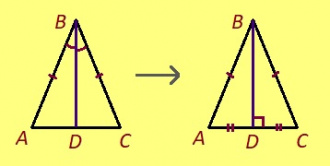
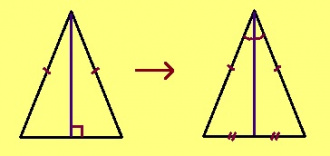
Теорема. Ӧткодь берда куимпельӧсаын йывса пельӧсыслӧн биссектриса лоӧ медианаӧн да судтаӧн.
Эскӧдӧм. Мед ABC – индӧм куимпельӧса, AB = BC, BD – биссектрисаыс. Сідзкӧ, ABD да CBD куимпельӧсаяс ӧткодьӧсь медводдза тӧдмӧс серти: AB = CB, ∠ABD = ∠CBD, BD – ӧтувъя дор. Та вӧсна AD = DC, ∠BDA = ∠BDC. Сіздкӧ, ∠BDA = ∠BDC = 90° кыдз орччаяс.
Куимпельӧсаяс ӧткодьлун йылысь коймӧд тӧдмӧс
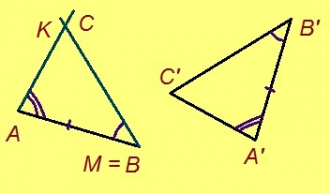
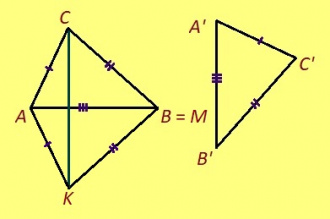
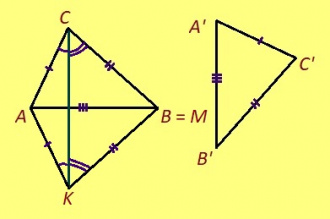
Теорема. Мед ABC да A’B’C’ – куимпельӧсаяс, AB = A’B’, BC = B’C’, AC = A’C’. Сэки ∆ABC = ∆A’B’C’.
Эскӧдӧм. Аксиома серти, эм сэтшӧм торъяланлуна AMK куимпельӧса: 1) ∆AMK = ∆A’B’C’; 2) AM куйлӧ AB визьньӧв пытшкын; 3) K да C чутъяс куйлӧны торъя тшӧтшкӧсджынъясын AB веськыд визь серти.
AB = A’B’ = AM, та вӧсна M = B.
AC = A’C’ = AK; сідзкӧ, AC да AK – боквыв доръяс ӧткодь берда CAK куимпельӧсаын. Та вӧсна ∠AKC = ∠ACK. Сэтшӧм жӧ ногӧн артмӧдам: ∠BKC = ∠BCK.
Сідзкӧ, ∠ACB = ∠ACK + ∠BCK = ∠AKC + ∠BKC = ∠AKB. Таысь кындзи, AC = AK, BC = BK. Сы вӧсна ABC да ABK куимпельӧсаяс ӧткодьӧсь медводдза тӧдмӧс серти да ∆A’B’C’ = ∆ABK = ∆ABC.
Веськыд визьысь ортсыын куйлысь чут пыр гижтӧм ӧшанвизь
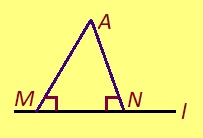
Теорема. Веськыд визьысь ортсыын куйлысь чут пыр оз позь нуӧдны кык торъялана ӧшанвизь.
Эскӧдӧм. Мед A чут лоӧ l веськыд визьысь ортсыын, AM да AN – кык торъялана ӧшанвизь, M да N чутъяс куйлӧны l-ын.
Аксиома серти, эм сэтшӧм торъяланлуна MBN куимпельӧса: 1) ∆MBN = ∆MAN, 2) A да B чутъяс куйлӧны торъя тшӧтшкӧсджынъясын l веськыд визь серти.
Миян артмӧ: ∠AMN = ∠BMN = 90°; та вӧсна ∠AMB = 180° да M чут куйлӧ AB веськыд визь вылын. Сэтшӧм жӧ ногӧн артмӧдам: N чут куйлӧ AB веськыд визь вылын. AB да l веськыдъяс вомӧнасьӧны сӧмын ӧти чутын. Сідзкӧ, M = N. Тайӧ кыв вожалӧм.
Кывкӧртӧд. Ӧткодь берда куимпельӧсаын йывса пельӧсысь нуӧдӧм судта лоӧ биссектрисаӧн да медианаӧн.
Эскӧдӧм (паныдсянь). Мед судтаыс оз ло биссектрисаӧн. Нуӧдам йывса пельӧслысь биссектрисасӧ. Сійӧ лоӧ судтаӧн. Сідзкӧ, йывса пельӧсысь позьӧ гижтыны подувлы ӧшанвизьлуна кык торъялана веськыд визь. Тайӧ кыв вожалӧм.
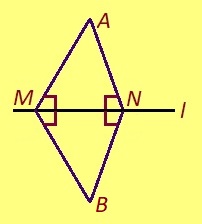
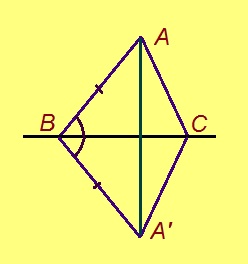
Теорема. Веськыд визьысь ортсыын куйлысь чут пыр позьӧ нуӧдны ӧшанвизь.
Эскӧдӧм. Мед A чут куйлӧ l веськыд визьысь ортсыын, B да C чутъяс лоӧны l вылын. Аксиома серти, эм BAC-кӧд ӧткодь BA’C куимпельӧса, A да A’ чутъясыс куйлӧны торъя тшӧтшкӧсджынъясын l веськыд визь серти. Сідзкӧ, ABA’ куимпельӧсаын AB = A’B, BC визьньӧв – ∠ABA’-лӧн биссектриса. Сідзкӧ, AA’ ӧшанвизьлуна l-лы.
Ортсыса пельӧс
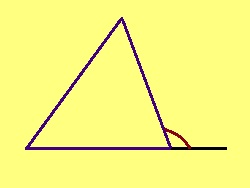
Урчитӧм. Куимпельӧсалӧн йыв бердын ортсыса пельӧсӧн шусьӧ индӧм йывса пельӧскӧд орчча пельӧс.
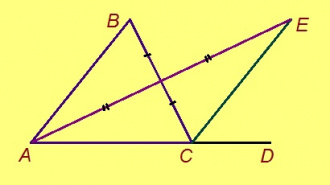
Теорема. Ортсыса пельӧс ыджыдджык куимпельӧсаса пельӧсысь, коді сыкӧд абу орчча.
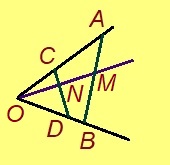
Эскӧдӧм. Мед ABC – куимпельӧса, ∠BCD лоӧ ∠BCA-кӧд орчча пельӧс (C чут куйлӧ A да D костын). Петкӧдлам: ∠ABC < ∠BCD.
Мед O чут – BC вундӧглӧн шӧр, E чут куйлӧ AO визьньӧв вылын, AO = OE. Сідзкӧ, ∆AOB = ∆EOC медводдза тӧдмӧс серти (∠AOB да ∠EOC – вертикаль пельӧсъяс да, найӧ ӧтыдждаӧсь). Та вӧсна ∠ABC = ∠BCE. O, B да E чутъяс куйлӧны ӧти тшӧтшкӧсджынйын AD веськыд визь серти. Миян артмӧ: ∠BCD = 180° – ∠BCA (кыдз орчча); ∠ABC = ∠BCE = ∠ACE – ∠BCA < 180° – ∠BCA. Та вӧсна ∠ABC < ∠BCD.
Куимпельӧса доръяс да пельӧсъяс ӧтластитӧм
Теорема. Куимпельӧсаын ыджыдджык дорлы паныд куйлӧ ыджыдджык пельӧс.
Эскӧдӧм. Мед ABC куимпельӧсаын AB < AC. Петкӧдлам: ∠B > ∠C. Мед D чут куйлӧ AC вундӧг вылын, AD = AB. Сідзкӧ, ∠ABD = ∠BDA. ∠BDA лоӧ ∆BCD куимпельӧсалӧн ортсыса пельӧс. Сідзкӧ, ∠BDA > ∠BCD. Миян артмӧ: ∠ABC > ∠ABD = ∠BDA > ∠BCD.
Кывкӧртӧд. Куимпельӧсаын ыджыдджык пельӧслы паныд куйлӧ ыджыдджык дор.
Сідзкӧ, куимпельӧсаын ӧти дор ыджыдджык мӧд дорысь сэк да сӧмын сэк, кор медводдза дорлы паныд куйлысь пельӧс ыджыдджык мӧд дорлы паныд куйлысь пельӧсысь.
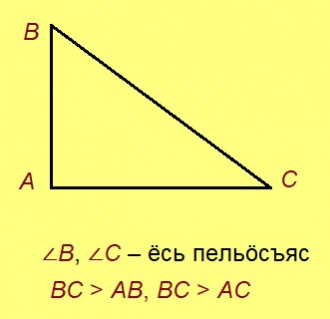
Теорема. 1) Веськыдпельӧса куимсэрӧгын гипотенузабердса пельӧсъяс ёсьӧсь. 2) Гипотенуза ыджыдджык катетысь.
Эскӧдӧм. 1) Веськыд пельӧскӧд орчча пельӧс веськыд; теорема серти, сійӧ ыджыдджык гипотенузабердса пельӧсысь. 2) Веськыд пельӧсыс куимпельӧсаын медыджыд, та вӧсна сылы паныд куйлысь дор медыджыд.
Висьталӧм. Тшӧтшыдпельӧса куимсэрӧгын эм кык ёсь пельӧс.
Эскӧдӧм. Ӧти пельӧсыс кӧ тшӧтшыд, сыкӧд орчча пельӧсыс ёсь. Куимпельӧсалӧн мукӧд пельӧсъяс тайӧ ортсыса пельӧссьыс ичӧтджыкӧсь; та вӧсна, найӧ ёсьӧсь.
Кывкӧртӧд. Ӧткодь берда куимпельӧсаын подувбердса пельӧсъяс ёсьӧсь.
Куимпельӧса ӧткодьтӧмлун
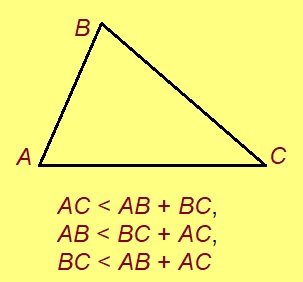
Теорема. Куимпельӧсалӧн кык дор кузьта содтасыс ыджыдджык коймӧд дор кузьтасьыс.
Эскӧдӧм. Мед ABC куимпельӧсаын AC дор медыджыд. Мед D чут куйлӧ AC вундӧг вылын, AB = AD.
Сідзкӧ, ∠ADB ёсь кыдз подув бердса пельӧс ӧткодь берда куимпельӧсаын. Та вӧсна ∠BDC тшӧтшыд. Миян артмӧ: BDC куимпельӧсаын ∠BDC медыджыд, сы понда BC > DC. Сідзкӧ, AC = AD + CD < AB + BC.
Ӧтнырвизя (параллель) веськыдъяс
Урчитӧм. Кык веськыд визь шусьӧ ӧтнырвизяӧн (параллельӧн), найӧ кӧ оз вомӧнасьны.
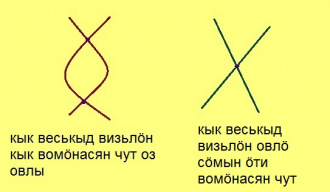
Теорема. Кык торъялана веськыд визь кӧ ӧшанвизьлунаӧсь коймӧд веськыдлы, найӧ ӧтнырвизяӧсь.
Эскӧдӧм (паныдсянь). Веськыд визьясыс кӧ вомӧнасьӧны, налӧн вомӧнасян чутысь позис эськӧ нуӧдны коймӧд веськыдӧ кык торъялана ӧшанвизь.
Кывкӧртӧд. Веськыд визьысь ортсыын куйлысь чут пыр позьӧ нуӧдны ӧтнырвизя веськыдсӧ.
Эскӧдӧм. Нуӧдам сетӧм A чутысь индӧм m веськыдӧ l ӧшанвизь. Сэсся A чут пыр нуӧдам l-лы ӧшанвизьлуна n веськыдсӧ. Миян артмӧ: l ӧшанвизьлуна m-лы да n-лы. Сідзкӧ, m да n ӧтнырвизяӧсь.
Параллельлун йылысь тӧдмӧсъяс
пытшкӧсса падвежӧнкуйлысь пельӧсъяс – внутренние накрест лежащие углы ортсыса падвежӧнкуйлысь пельӧсъяс – внешние накрест лежащие углы весьтаса пельӧсъяс – соответственные углы пытшкӧсса ӧтарбокса пельӧсъяс – внутренние односторонние углы ортсыса ӧтарбокса пельӧсъяс – внешние односторонние углы
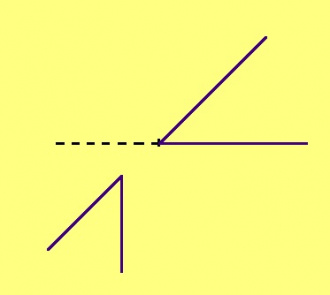
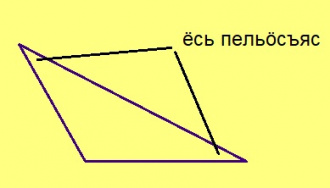
Сетӧма торъялана кык веськыд визь да найӧс вундысь (накӧд вомӧнасьысь веськыд визь). Пытшкӧсса падвежӧнкуйлысь пельӧсъяс, ортсыса падвежӧнкуйлысь пельӧсъяс, весьтаса пельӧсъяс, пытшкӧсса ӧтарбокса пельӧсъяс, ортсыса ӧтарбокса пельӧсъяс петкӧдлӧмаӧсь серпас вылын.
Теорема. Сетӧма кык веськыд визь да найӧс вундысь. Артмӧм пытшкӧсса падвежӧнкуйлысь пельӧсъяс кӧ ӧтыдждаӧсь, веськыдъясыс ӧтнырвизяӧсь.
Эскӧдӧм. Мед AC да BD – сетӧм веськыдъяс, AB – вундысь, ∠ABD = ∠BAC. Мед M – AB вундӧглӧн шӧр. Нуӧдам M чут пыр AC веськыдӧ MP ӧшанвизь. Мед сійӧ вомӧнасьӧ BD-кӧд Q чутын. ∠AMP = ∠BMQ кыдз сувтсаяс. Сідзкӧ, ∆AMP = ∆BMQ мӧд тӧдмӧс серти. Та вӧсна ∠BQM = ∠APM = 90°. Миян артмӧ: BQ да AP веськыдъяс ӧшанвизьлунаӧсь PQ веськыдлы. Сідзкӧ, найӧ ӧтнырвизяӧсь.
Кывкӧртӧд. Сетӧма кык веськыд визь да найӧс вундысь. Артмӧм ортсыса падвежӧнкуйлысь пельӧсъяс кӧ ӧтыдждаӧсь, веськыдъясыс ӧтнырвизяӧсь.
Эскӧдӧм. Мед ∠1, ∠2 – ортсыса падвежӧнкуйлысь пельӧсъяс, ∠1 = ∠2. ∠1 = ∠3, ∠2 = ∠4 кыдз сувтсаяс. Сідзкӧ, ∠3 = ∠4. Тайӧ пельӧсъясыс – пытшкӧсса падвежӧнкуйлысьяс. Сідзкӧ, веськыдъясыс ӧтнырвизяӧсь.
Кывкӧртӧд. Сетӧма кык веськыд визь да найӧс вундысь. Артмӧм пытшкӧсса (ортсыса) ӧтарбокса пельӧсъяс содтасыс кӧ 180° ыджда, веськыдъясыс ӧтнырвизяӧсь.
Эскӧдӧм. Мед ∠1, ∠2 – пытшкӧсса ӧтарбокса пельӧсъяс, ∠1 + ∠2 = 180°. ∠2 да ∠3 орччаӧсь, та вӧсна ∠2 + ∠3 = 180°. Сідзкӧ, ∠1 = ∠3. ∠1 да ∠3 пытшкӧсса падвежӧнкуйлысьяс; теорема серти, сетӧм веськыдъясыс ӧтнырвизяӧсь. Ортсыса ӧтарбокса пельӧсъяс содтасыс кӧ 180° ыджда, подулалам кывкӧртӧдсӧ сэтшӧм жӧ ногӧн.
Кывкӧртӧд. Сетӧма кык веськыд визь да найӧс вундысь. Весьтаса пельӧсъяс кӧ ӧтыдждаӧсь, веськыдъясыс ӧтнырвизяӧсь.
Эскӧдӧм. Мед ∠1, ∠2 – весьтаса пельӧсъяс, ∠1 = ∠2. ∠1 да ∠3 сувтсаяс, та вӧсна ∠1 = ∠3. Сідзкӧ, пытшкӧсса падвежӧнкуйлысь пельӧсъяс, ∠2 да ∠3, ӧтыдждаӧсь. Теорема серти, веськыдъясыс ӧтнырвизяӧсь.
Параллель веськыд йылысь аксиома
Аксиома. Веськыд визьысь ортсыын куйлысь чут пыр позьӧ нуӧдны сӧмын ӧти ӧтнырвизя веськыдӧс.
Кывкӧртӧд. Кык торъялана веськыд визь кӧ ӧтнырвизяӧсь коймӧд веськыдкӧд, найӧ ӧтнырвизяӧсь ӧта-мӧдыскӧд.
Эскӧдӧм. Мед a да b веськыдъяс ӧтнырвизяӧсь c веськыдкӧд да вомӧнасьӧны M чутын. Сідзкӧ, M чут пыр позьӧ нуӧдны кык торъялана веськыд визь, кодъяс c-кӧд ӧтнырвизяӧсь. Аксиома серти, позьӧ нуӧдны сӧмын ӧтиӧс. Тайӧ кыв вожалӧм.
Параллель веськыдъяс торъяланлунъяс
Теорема. Сетӧма кык ӧтнырвизя веськыд да найӧс вундысь. Сэки артмӧм пытшкӧсса падвежӧнкуйлысь пельӧсъяс ӧтыдждаӧсь.
Эскӧдӧм. Мед ∠DAB да ∠CBA абу ӧтыдждаӧсь. Нуӧдам A чут пыр AE веськыдӧс сідзи, медым ∠EAB = ∠CBA. Сідзкӧ, EA да BC веськыдъяс ӧтнырвизяӧсь. Та вӧсна A чут пыр мунӧ BC-кӧд ӧтнырвизя кык веськыд: AD да AE. Тайӧ кыв вожалӧм.
Кывкӧртӧд. Сетӧма кык ӧтнырвизя веськыд да найӧс вундысь. Сэки 1) артмӧм ортсыса падвежӧнкуйлысь пельӧсъяс ӧтыдждаӧсь; 2) артмӧм весьтаса пельӧсъяс ӧтыдждаӧсь; 3) артмӧм пытшкӧсса ӧтарбокса пельӧсъяс содтасыс 180° ыджда; 4) артмӧм ортсыса ӧтарбокса пельӧсъяс содтасыс 180° ыджда.