Унабана йылысь Эйлер теорема — различия между версиями
Наста (сёрнитанін | чӧжӧс) |
Наста (сёрнитанін | чӧжӧс) |
||
| Строка 89: | Строка 89: | ||
Мед унабана абу мылькъя, но сылӧн веркӧсыс “сфера сяма”: нюжӧдӧмӧн да топӧдӧмӧн (но орйӧдлытӧг да лемавтӧг) сыысь позьӧ вӧчны сфера. Вӧлӧмкӧ, сэки Эйлер теорема лӧсялӧ. | Мед унабана абу мылькъя, но сылӧн веркӧсыс “сфера сяма”: нюжӧдӧмӧн да топӧдӧмӧн (но орйӧдлытӧг да лемавтӧг) сыысь позьӧ вӧчны сфера. Вӧлӧмкӧ, сэки Эйлер теорема лӧсялӧ. | ||
| + | |||
| + | [[Файл:Aby mylkja1.jpg|thumb|center|440px|]] | ||
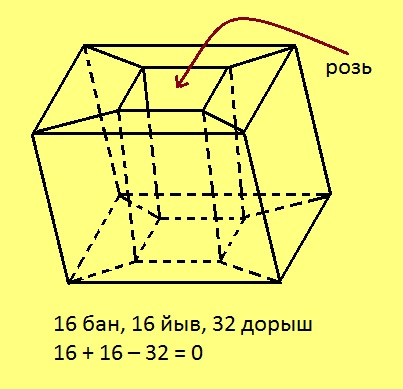
Веркӧсыс кӧ абу “сфера сяма” (шуам, сійӧ ӧшинь рама кодь), теорема торксьӧ. | Веркӧсыс кӧ абу “сфера сяма” (шуам, сійӧ ӧшинь рама кодь), теорема торксьӧ. | ||
| + | |||
| + | [[Файл:Tor .jpg|thumb|center|440px|]] | ||
[[Category:Математика]] | [[Category:Математика]] | ||
Версия 21:41, 25 кӧч 2018
Терминъяс
мылькъя унабана – выпуклый многогранник бан – грань дорыш – ребро йыв – вершина мыччӧд – пример тшӧтшкӧс – плоскость, плоский унапельӧса – многоугольник вундӧг – отрезок висьталӧм – утверждение
Эйлер теорема
Эйлер теорема. Мед мылькъя унабаналӧн b бан, d дорыш да j йыв. Сэки b + j – d = 2.
Медводз видлалам некымын мыччӧд.
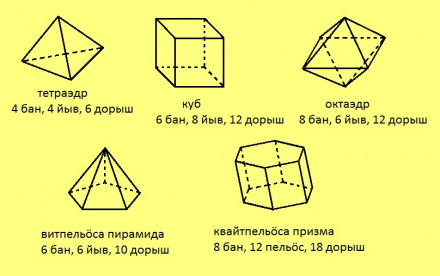
Тетраэдрлӧн 4 бан, 4 йыв, 6 дорыш; b + j – d = 4 + 4 – 6 = 2.
Кублӧн 6 бан, 8 йыв, 12 дорыш; b + j – d = 6 + 8 – 12 = 2.
Витпельӧса пирамидалӧн 6 бан, 6 йыв, 10 дорыш; b + j – d = 6 + 6 – 10 = 2.
Квайтпельӧса призмалӧн 8 бан, 12 йыв, 18 дорыш; b + j – d = 8 + 12 – 18 = 2.
Октаэдрлӧн 8 бан, 6 йыв, 12 дорыш; b + j – d = 8 + 6 – 12 = 2.
Эйлер эскӧдӧмын тыдовтчисны тырмытӧмторъяс. Колана ногӧн теоремасӧ вермис подулавны прансуз Огюстен Луи Коши. Математиклӧн шӧр мӧвпыс вӧлі татшӧм.
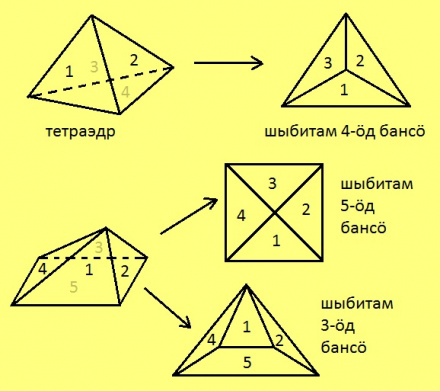
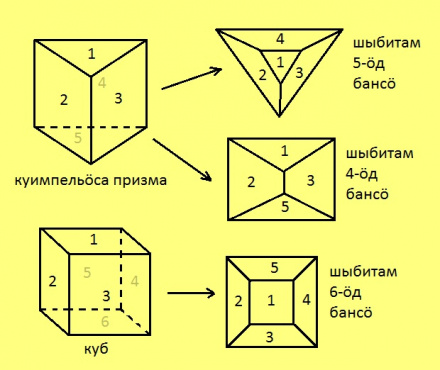
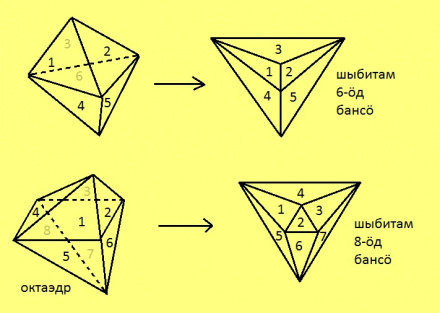
Унабанасӧ “лямӧдам” либӧ “нюжӧдам” да видзӧдлам “артмӧм” тшӧтшкӧс серпас. Думыштам, мый унабанасӧ вӧчӧма резинаысь да быд дорышті ручкаӧн нуӧдӧма визь. Ӧти бансӧ вундам, а кольӧм веркӧссӧ нюжӧдам сідзи, медым сійӧ лои тшӧтшкӧсӧн да быд чертитӧм визь лои вундӧгӧн.
Петкӧдлам некымын пример.
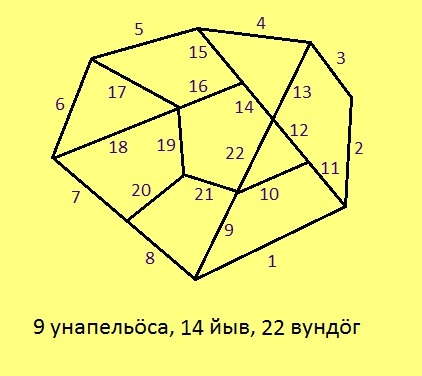
Мед унабаналӧн эм b бан, d дорыш да j йыв. Тшӧтшкӧс серпас вылын лоӧ b – 1 унапельӧса, d вундӧг да j йыв. (Ӧти бан ми вундім, а йыв-дорышсӧ колим.) Сідзкӧ, миянлы колӧ петкӧдлыны: (b – 1) + d – j = 1.
Висьталӧм. Мед унапельӧсасӧ юклӧма u мылькъя унапельӧса вылӧ; тайӧ фигураын ставыс лоӧ v вундӧг да j йыв. Сэки u + j – v = 1.
Эскӧдӧм идеяыс татшӧм. Ми некымынысь содтам либӧ чышкам вундӧгъяс да йывъяс сідзи, медым u + j – v лыд эз вежсьы, да бӧръяпомыс миян артмас ӧти куимпельӧса.
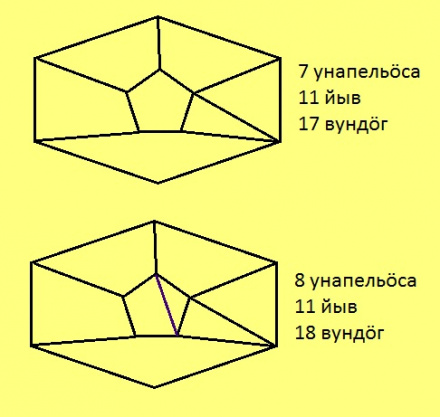
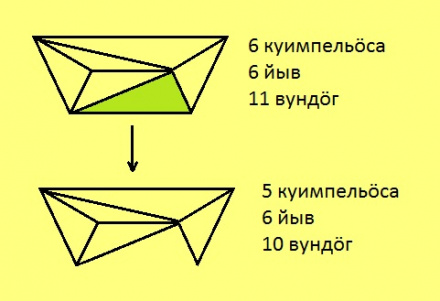
Куимпельӧсаяс вылӧ юклӧм. Босьтам ӧти унапельӧса да нуӧдам сылысь кутшӧмкӧ диагональ. Воддза серпасын кӧ вӧлі u = m, j = n, v = k, выль серпасын лоас u = m + 1, j = n да v = k + 1.
Сідзкӧ, выль серпасын u + j – v = (m + 1) + n – (k + 1) = m + n – k. Та вӧсна диагональ нуӧдӧм бӧрын u + j – v лыд оз вежсьы.
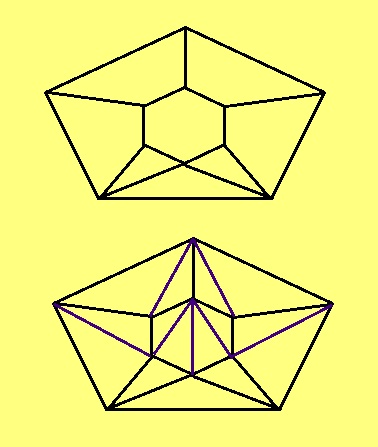
Диагональяс нуӧдігӧн став унапельӧсасӧ юклам некымын куимпельӧса вылӧ.
Куимпельӧса чышкалӧм. Мед унапельӧса юклӧма u куимпельӧса вылӧ; тайӧ серпасын ставыс лоӧ v вундӧг да j йыв. Миянлы колӧ петкӧдлыны: u + j – v = 1.
Босьтам куимпельӧса, кодлӧн кӧть ӧти дор оз куйлы унапельӧса пытшкас, да чышкам сійӧс. Мыйла u + j – v оз вежсьы?
Мед u = m, j = n, v = k. Видлам кык ног.
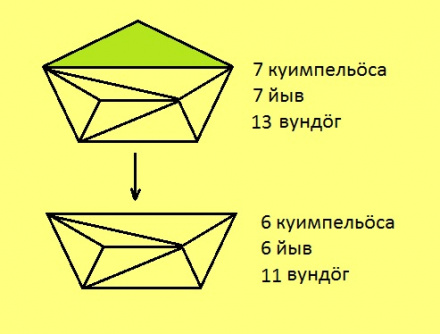
1) Чышкӧм куимпельӧсаыслӧн кык дор оз куйлы унапельӧса пытшкас. Сэки ми чышкам ӧти куимпельӧса, ӧти йыв да кык дор; выль серпасын u + j – v = (m – 1) + (n – 1) – (k – 2) = m + n – k.
2) Чышкӧм куимпельӧсалӧн сӧмын ӧти дор оз куйлы унапельӧса пытшкас. Сэки ми чышкам ӧти куимпельӧса да ӧти вундӧг; выль серпасын u + j – v = (m – 1) + n – (k – 1) = m + n – k.
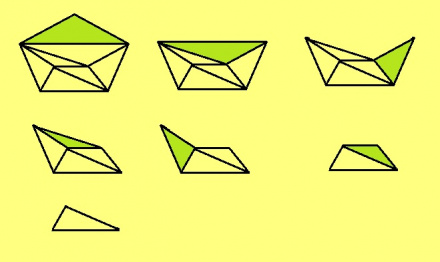
Куимпельӧсаяссӧ сьӧрсьӧн-бӧрсьӧн чышкалам да бӧръяпомыс миян коляс ӧти куимпельӧса.
Лоас u = 1, j = 3, v = 3, та вӧсна u + j – v = 1 + 3 – 3 = 1. Тайӧн эскӧдӧмсӧ сигӧртам.
Мый лоас, унабана кӧ абу мылькъя?
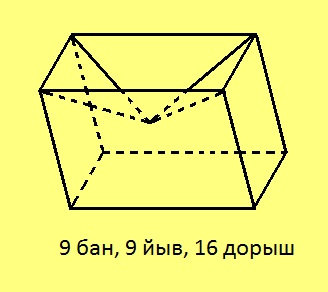
Мед унабана абу мылькъя, но сылӧн веркӧсыс “сфера сяма”: нюжӧдӧмӧн да топӧдӧмӧн (но орйӧдлытӧг да лемавтӧг) сыысь позьӧ вӧчны сфера. Вӧлӧмкӧ, сэки Эйлер теорема лӧсялӧ.
Веркӧсыс кӧ абу “сфера сяма” (шуам, сійӧ ӧшинь рама кодь), теорема торксьӧ.