Планиметрия курс

Веськыд визь йылысь аксиомаяс

тшӧтшкӧс – плоскость
веськыд визь – прямая
чут – точка
мыгӧр – фигура
кывкӧртӧд – следствие
эскӧдӧм – доказательство
кыв вожалӧм – противоречие

Планиметрия – тайӧ тшӧтшкӧс пытшкын куйлысь мыгӧръяс тӧдмалан геометрия юкӧн.

Тшӧтшкӧслысь, веськыд визьлысь, чутлысь медшӧр торъяланлунъяссӧ индам аксиомаяс пыр.

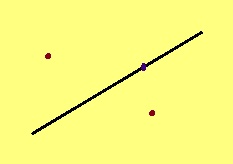
Аксиома. Эм кӧ тшӧтшкӧсын веськыд визь, сэк тшӧтшкӧсса чутъяс пӧвстысь кодсюрӧяс лоасны тайӧ визьын, а мукӧдыс сыысь ортсын.

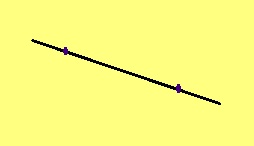
Аксиома. Кык торъя чут пыр позьӧ нуӧдны веськыд визь да сӧмын ӧтиӧс.

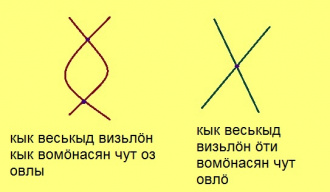
Кывкӧртӧд. Кык торъя веськыдлӧн кӧ эм вомӧнасян чут, тайӧ чутыс ӧтка.

Эскӧдӧм. Мед веськыд визьясыс вомӧнасьӧны торъя кык чутын. Сідзкӧ, тайӧ чутъяс пырыс мунӧ торъя кык веськыд визь. Аксиома серти, позьӧ нуӧдны сӧмын ӧти веськыд визьӧс. Тайӧ кыв вожалӧм.

Вундӧг

вундӧг – отрезок

Аксиома. Ӧти веськыд визь вылын куйлысь торъя куим чут пиысь ӧти да сӧмын ӧти чут куйлӧ мӧд кык чут костын.

Кык чут на костын став куйлысь чутъяскӧд артмӧдӧны вундӧг.

Аксиома. Быд вундӧглӧн эм кузьта – плюса лыд.

Вундӧг кӧ артмӧдӧма A да B чутъясӧн, пасъям сійӧс AB; сідзи жӧ пасъям сылысь кузьтасӧ. A да B чутъясыс шусьӧны AB вундӧг помъясӧн.

Аксиома. Мед торъя A, B да C чутъяс куйлӧны ӧти веськыд визь вылын, B куйлӧ A да C костын. Сэки AC = AB + BC.

Кывкӧртӧд. Мед торъя A, B да C чутъяс куйлӧны ӧти веськыд визь вылын, B куйлӧ A да C костын. Сэки AC > AB, AC > BC.

Кывкӧртӧд. Мед торъя A, B да C чутъяс куйлӧны ӧти веськыд визь вылын, AC = AB + BC. Сэки B куйлӧ A да C костын.

Эскӧдӧм. Миян артмӧ: AC > AB, AC > BC. A чут кӧ куйлӧ B да C костын, BC > AC; C чут кӧ куйлӧ A да B костын, AB > AC. Сідзкӧ, B куйлӧ A да C костын.