Фудзиталӧн аксиомаяс йылысь

Терминъяс

ӧткодь доръяса куимпельӧса – равносторонний треугольник
бур унапельӧса – правильный многоугольник
вундӧг – отрезок

Фудзиталӧн аксиомаяс

Аксиомаяссӧ позьӧ аддзыны татысь.

Мый нӧшта артмӧдны Фудзиталӧн медводдза нёль аксиомаӧн вӧдитчӧмӧн?

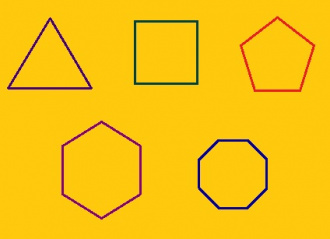
Позьӧ артмӧдны квадрат да ӧткодь доръяса куимпельӧса. Лӧсьӧдім кӧ квадрат да ӧткодь доръяса куимпельӧса – та бӧрын бур квайтпельӧса да бур кӧкъямыспельӧса артмӧдны абу нин сьӧкыд.

Дай бур витпельӧса тшӧтш позьӧ лӧсьӧдны куш нёль аксиоманас вӧдитчӧмӧн.

Тайӧ этша на. Нёль аксиома кежысь позьӧ оз сӧмын бур унапельӧсаяссӧ артмӧдны, а и пропорциялы вундӧг корсьны. Петкӧдлам, кыдзи вӧчны тайӧс.

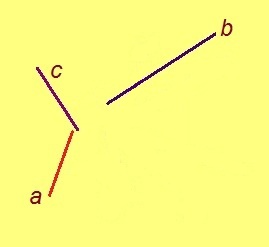
Тшӧтшкӧс вылын куим вундӧг гижтӧма: a, b, c. Колӧ артмӧдны нёльӧд вундӧг (пасъям сійӧс x-ӧн), медым a : b = c : x.

1. Кабаласӧ кусыньтӧмӧн артмӧдам кутшӧмкӧ пельӧс (серпасас сійӧ сьӧд рӧмӧн гижтӧма).

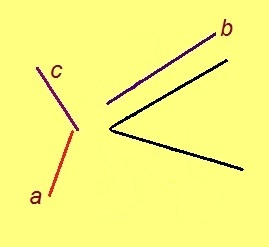
Пельӧс йылас пуктам a, b да c-лысь ӧти помнысӧ (тайӧс позьӧ вӧчны кабала кусыньтӧмӧн жӧ, 2-ӧд аксиома серти). Артмасны a’ = a, b’ = b, c’ = c вундӧгъяс.

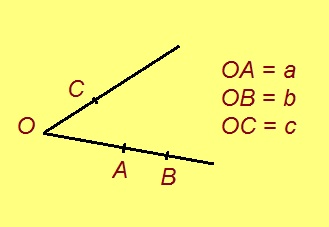
2. a’ да b’ вундӧгъяссӧ ӧти пельӧс дор вылӧ пуктам, c’ вундӧгсӧ – мӧд дор вылас (3-ӧд аксиома серти).

Артмӧ: OA = a, OB = b, OC = c.

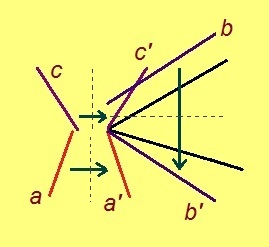
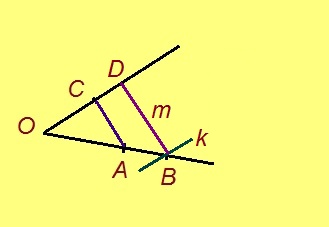
3. A да C чутъяс пыр веськыд визь нуӧдам (1-ӧд аксиома серти). Сэсся B чут пыр AC-лы перпендикуляр гижтам (4-ӧд аксиома серти). Пасъям сійӧс k-ӧн. Сы бӧрын B чут пыр k-лы перпендикуляр нуӧдам (пасъям сійӧс m-ӧн). Миян артмӧ: m да AC – параллель нога визьяс.

OC да m вомӧнасьӧны D чутын. Фалес теорема серти, OA : OB = OC : OD, либӧ a : b = c : OD.

Со корсянторыс и сюрӧма.

Содтӧд юӧр

Велӧдӧм паськӧдан блогын - 1.