Кыдзи оригами ногӧн ыдждӧдны куб кык пӧв — различия между версиями
Наста (сёрнитанін | чӧжӧс) (Новая страница: «==Терминъяс== веськыдсэрӧг – прямоугольник вундӧг – отрезок ӧтсяма куимпельӧсаяс – по…») |
Наста (сёрнитанін | чӧжӧс) (→Артмӧдӧм) |
||
| Строка 11: | Строка 11: | ||
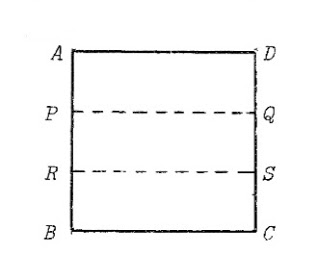
1. Гижтам ''ABCD'' квадрат да юклам сійӧс ӧткодь куим веськыдсэрӧг вылӧ: ''ADQP'', ''PQSR'' да ''RSCB''. | 1. Гижтам ''ABCD'' квадрат да юклам сійӧс ӧткодь куим веськыдсэрӧг вылӧ: ''ADQP'', ''PQSR'' да ''RSCB''. | ||
| + | |||
| + | [[Файл:Figure1.jpg|thumb|center|330px|]] | ||
2. Кабаласӧ кусыньтам сідзи, медым ''C'' чут веськаліс ''AB'' дор вылӧ, а ''S'' чут лоис ''PQ'' вундӧг вылын (Фудзиталӧн 6-ӧд аксиома серти). | 2. Кабаласӧ кусыньтам сідзи, медым ''C'' чут веськаліс ''AB'' дор вылӧ, а ''S'' чут лоис ''PQ'' вундӧг вылын (Фудзиталӧн 6-ӧд аксиома серти). | ||
Версия 00:27, 14 йирым 2020
Содержание
Терминъяс
веськыдсэрӧг – прямоугольник вундӧг – отрезок ӧтсяма куимпельӧсаяс – подобные треугольники
Артмӧдӧм
Оригами ногӧн позьӧ вӧчны кык вундӧг, кодъяс лӧсялӧны ∛2 да 1 моз. Та вӧсна позьӧ и куб кык пӧв ыдждӧдны.
Артмӧдны татшӧм кык вундӧг вӧзйӧма Питер Месснер Crux Mathematicorum журналын 1985-ӧд воын (гижӧма лыддьысьысьяслы задача пыдди). А мыйла буретш тадзи колӧ вӧчны, вӧлі гӧгӧрвоӧдӧма сёрӧнджык, 1986-ӧд воын.
1. Гижтам ABCD квадрат да юклам сійӧс ӧткодь куим веськыдсэрӧг вылӧ: ADQP, PQSR да RSCB.
2. Кабаласӧ кусыньтам сідзи, медым C чут веськаліс AB дор вылӧ, а S чут лоис PQ вундӧг вылын (Фудзиталӧн 6-ӧд аксиома серти).
Вӧлӧмкӧ, AC : BC = ∛2.
Подулалӧм
Дзоньнас подулалӧмсӧ ог вайӧд, сӧмын идеясӧ петкӧдла.
Казялам: SPC да CBT куимпельӧсаяс ӧтсямаӧсь кык пельӧс серти (∠CTB = 90° – ∠TCB = ∠SCP). Сідзкӧ, CS : PC = CT : BT.
Мед CB = 1, AC = x, BT = y. Сідзкӧ, CT = 1 + x – y, CS = (1 + x)/3, CP = (2x – 1)/3. Та вӧсна артмӧ пропорция:
(1 + x) : (2x – 1) = (1 + x – y) : y.
Пифагор теорема серти, 1 + y2 = (1 + x – y)2. Медбӧръя кык ӧткодьлунысь позьӧ петкӧдны: x3 = 2.