Планиметрия курс

Веськыд визь йылысь

тшӧтшкӧс – плоскость
веськыд визь – прямая
чут – точка
мыгӧр – фигура
кывкӧртӧд – следствие
эскӧдӧм – доказательство
кыв вожалӧм – противоречие

Планиметрияӧн шусьӧ геометриялӧн юкӧн, кӧні велӧдӧны тшӧтшкӧсвывса мыгӧръяс.

Тшӧтшкӧслысь, веськыд визьлысь, чутлысь медшӧр торъяланлунъяссӧ индам аксиомаяс пыр.

Аксиома. Эм кӧ тшӧтшкӧсын веськыд визь, сэк тшӧтшкӧсса чутъяс пӧвстысь кодсюрӧяс лоасны тайӧ визьын, а мукӧдыс сыысь ортсын.

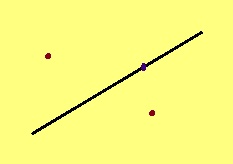
Аксиома. Кык торъялана чут пыр позьӧ нуӧдны веськыд визь; татшӧм визьыс овлӧ сӧмын ӧти.

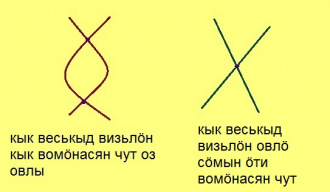
Кывкӧртӧд. Вомӧнасьӧны кӧ кык торъялана веськыд визь, вомӧнасян чутныс лоӧ сӧмын ӧти.

Эскӧдӧм. Мед, шуам, веськыд визьясыс вомӧнасьӧны торъялана кык чутын. Сідзкӧ, тайӧ чутъяс пырыс позьӧ гижтыны кык торъялана веськыд визь. А аксиомаыд серти, татшӧм визьыс на пыр вермас мунны сӧмын ӧти. Артмӧ кыв вожалӧм.

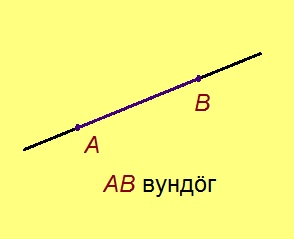
Вундӧг

вундӧг – отрезок

Аксиома. Ӧти веськыд визьса куим торъялан чут пиысь ӧтиыс лоӧ мӧд кык костас; татшӧм чутыс овлӧ сӧмын ӧти.

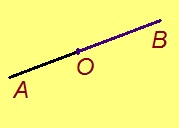
Кык чут на костса став чутыскӧд ӧтув артмӧдӧны вундӧг. Индӧм кык чутыс шусьӧны вундӧг помъясӧн.

Аксиома. Быд вундӧглӧн эм кузьта – плюса лыд.

Вундӧг помъясын кӧ А да В чутъяс, шуам татшӧм вундӧгсӧ АВ; тадзи жӧ и сылысь кузьтасӧ шуам.

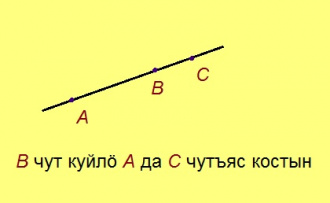
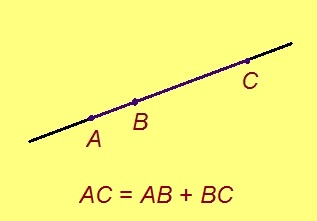
Аксиома. Мед ӧти веськыд визьын эм куим торъя чут: A, B да C; B-ыс куйлӧ A да C костас. Сэки AC = AB + BC.

Кывкӧртӧд. Мед ӧти веськыд визьын эм куим торъя чут: A, B да C; B-ыс куйлӧ A да C костас. Сэки AC > AB, AC > BC.

Кывкӧртӧд. Мед ӧти веськыд визьын эм куим торъя чут: A, B да C; AC = AB + BC. Сэки B-ыс куйлӧ A да C костас.

Эскӧдӧм. Миян артмӧ: AC > AB, AC > BC. A чутыс кӧ куйлӧ B да C костас, BC > AC; C чутыс кӧ куйлӧ A да B костас, AB > AC. Сідзкӧ, B-ыс куйлӧ A да C костас.

Тшӧтшкӧсджын

тшӧтшкӧсджын – полуплоскость

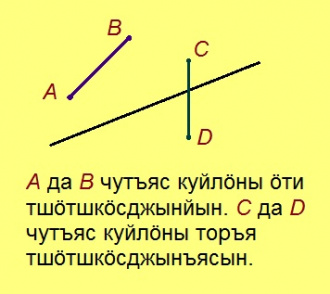
Аксиома. Быд веськыд визь юклӧ тшӧтшкӧссӧ кык тшӧтшкӧсджын вылӧ. Кык чут A да B куйлӧны ӧти тшӧтшкӧсджынйын, оз кӧ AB вундӧгыс вомӧнав индӧм веськыд визьсӧ.

Сідзкӧ, AB-ыс кӧ вомӧналӧ тайӧ веськыд визьсӧ, A да B чутъясыс куйлӧны торъя тшӧтшкӧсджынъясын.

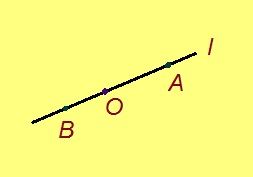
Аксиома. Сетӧма кӧ l веськыд визь да сы вылын куйлысь O чут, быть сюрасны и сэтшӧм A да B чутъяс, кодъяслы лӧсялӧ татшӧмтор: A, O, B абу ӧтилаынӧсь, A да B куйлӧны l вылын да O чутыс куйлӧ A да B чутъяс костын.

Визьньӧв

визьньӧв – луч
веськыд визьджын – полупрямая

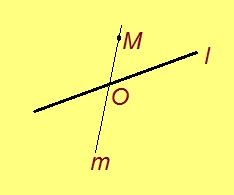
Мед O чут куйлӧ l веськыд визь вылын. Босьтам l сайын куйлысь M чутсӧ. Нуӧдам O да M чутъяс пыр m веськыд визьсӧ. Сэки m юклӧ тшӧтшкӧссӧ кык тшӧтшкӧсджын вылӧ.

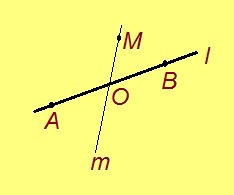
Мед A да B чутъяс куйлӧны l веськыд визь вылын. Аксиома серти, найӧ куйлӧны торъя тшӧтшкӧсджынъясын сэк да сӧмын сэк, кор O чут куйлӧ AB вундӧгын. Сідзкӧ, O чут юклӧ l веськыдсӧ кык юкӧн вылӧ; тайӧ юкӧнъясыс шусьӧны визьньӧвъясӧн либӧ веськыд визьджынъясӧн.

OA да OB – кык визьньӧв:

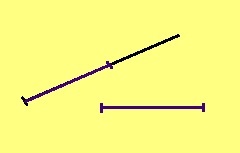
Аксиома. Быд визьньӧвйӧ сы йывсяньыс сетӧм кузьтаӧн позьӧ гижтыны дзик ӧти вундӧг.

Пельӧс йылысь

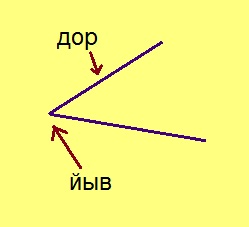
пельӧс – угол
пельӧс дор – сторона угла
пельӧс йыв – вершина угла
павтыртӧм пельӧс – развёрнутый угол
ёсь пельӧс – острый угол
веськыд пельӧс – прямой угол
ныж пельӧс – тупой угол
орчча пельӧсъяс – смежные углы
вертикаль пельӧсъяс – вертикальные углы

Ӧти чутысь петысь кык визьньӧв артмӧдӧны пельӧс. Тайӧ визьньӧвъясыс шусьӧны пельӧс доръясӧн, а налӧн ӧтувъя чутыс – пельӧс йылӧн.

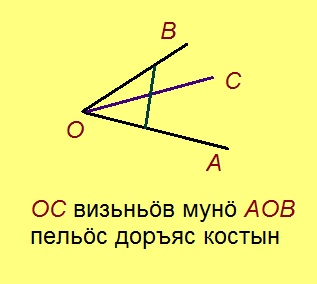
Пельӧс доръяс костса визьньӧв

Урчитӧм. Визьньӧв мунӧ пельӧс доръяс костӧд, сылӧн помыс кӧ лӧсялӧ пельӧс йывкӧд да сійӧ кӧ вомӧнасьӧ кутшӧмкӧ вундӧгкӧд, кодлӧн помъясыс куйлӧны пельӧс доръяс вылас.

Висьталӧм. Визьньӧв кӧ мунӧ пельӧс доръяс костӧд, сійӧ вомӧнасьӧ быд вундӧгкӧд, кодлӧн помъясыс куйлӧны пельӧс доръяс вылас.

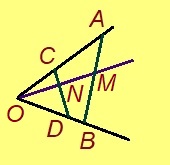
Эскӧдӧм. Мед O – кутшӧмкӧ пельӧслӧн йыв, OM – визьньӧв, коді мунӧ пельӧс доръяс костӧд. Урчитӧм серти, OM вомӧнасьӧ кутшӧмкӧ AB вундӧгкӧд, кӧні A да B чутъясыс куйлӧны пельӧс доръяс вылас. Мед CD – мӧд вундӧг, C куйлӧ OA визьньӧв вылын, D куйлӧ OB визьньӧв вылын.

OM веськыд визь юкӧ тшӧтшкӧссӧ кык тшӧтшкӧсджынйӧ; аксиома серти, A да B чутъяс оз ӧти тшӧтшкӧсджынас куйлыны. A да C чутъяс куйлӧны OA визьньӧв вылын, та вӧсна найӧ куйлӧны ӧти тшӧтшкӧсджынйын, OM веськыд визь серти кӧ. Сідзи жӧ артмӧ: B да D чутъяс куйлӧны ӧти тшӧтшкӧсджынйын, OM веськыд визь серти жӧ. Сідзкӧ, CD вундӧг вомӧнасьӧ OM веськыд визьыскӧд. Пасъям вомӧнасян чутсӧ N шыпасӧн.

Петкӧдлам, мый ОМ веськыд визьвывса N чут куйлӧ ОМ визьньӧв вылын. N кӧ тайӧ визьньӧв вылас эз куйлы, O чут куйліс эськӧ M да N костын. Сэки, босьтам кӧ тшӧтшкӧссӧ кык джынйӧ юкысь пыдди OB веськыд визь, M да N эз эськӧ куйлыны ӧти тшӧтшкӧсджынас. Но CA, CN, AM вундӧгъяс оз вомӧнасьны OB веськыд визьыскӧд. Сідзкӧ, OB веськыд визь серти кӧ, N, C, A, М чутъяс куйлӧны ӧти тшӧтшкӧсджынйын. Артмис кыв вожалӧм.

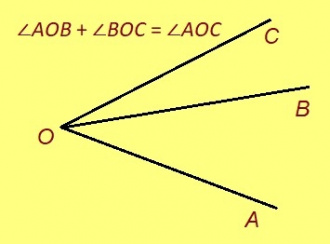
Пельӧс градуса муртӧс

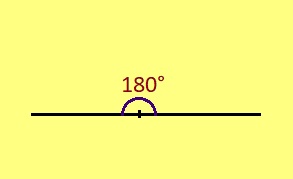
Урчитӧм. Пельӧслӧн доръясыс кӧ артмӧдӧны веськыд визь, сійӧ шусьӧ павтыртӧм пельӧсӧн.

Аксиомаяс. 
1. Быд пельӧс позьӧ муртавны плюса градусӧн. 
2. Визьньӧв кӧ мунӧ пельӧс доръяс костӧд, сэки тайӧ пельӧсас сымда жӧ градус, мыйта визьньӧвнас артмӧдӧм кыкнан пельӧсас ӧтув босьтӧмӧн.

3. Павтыртӧм пельӧсыс лоӧ 180° ыджда.

4. Быд визьньӧвсянь позьӧ бӧрйӧм тшӧтшкӧсджынйӧ пуктыны сетӧм муртӧсӧн дзик ӧти пельӧс (медтыкӧ 180°-ысь ыджыдджык эз вӧв-а).

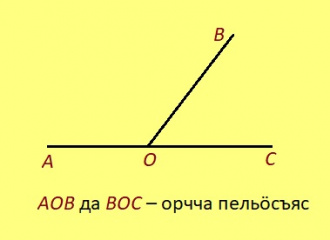
Орчча пельӧсъяс

Урчитӧм. Кык пельӧс шусьӧ орччаӧн, налӧн кӧ эм ӧтувъя дор, а мӧд доръяс кӧ артмӧдӧны веськыд визь.

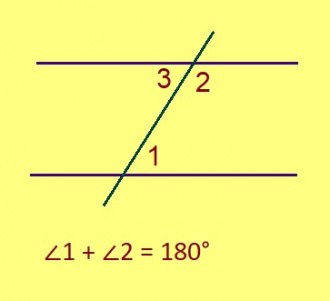
Теорема. Ӧтувтам кӧ орчча пельӧсъяслысь ыджданысӧ, лоӧ 180°.
Эскӧдӧм. Орчча пельӧсъяс артмӧдӧны павтыртӧм пельӧссӧ, кодлӧн ыдждаыс 180°. Сідзкӧ, 2-ӧд аксиома серти, налӧн суммаыс лоас 180°.
Кывкӧртӧд.  Пельӧсыс кӧ 90° ыджда, сыкӧд орчча пельӧсыс сідзжӧ 90° ыджда.

Бур (веськыд), ёсь да ныж пельӧсъяс

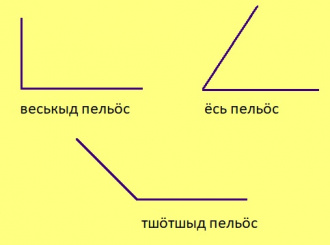
Урчитӧм. Пельӧс шусьӧ ёсьӧн, сылӧн градуса муртӧсыс кӧ 90°-ысь этшаджык; бур пельӧсӧн (рочӧн моз веськыд пельӧс), сійӧ кӧ 90° ыджда; ныж пельӧсӧн, сійӧ кӧ 90°-ысь ыджыдджык.

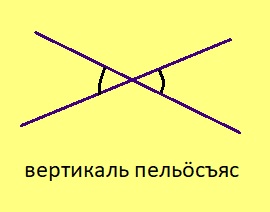
Вертикаль пельӧсъяс

Урчитӧм. Кык пельӧс шусьӧ вертикаль пельӧсъясӧн, ӧтиыслӧн доръясыс кӧ лоӧны мӧд пельӧсса доръяслӧн нюжӧдӧмӧн.

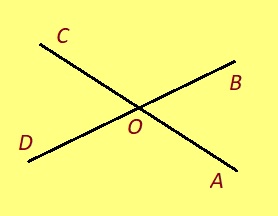
Теорема. Вертикаль пельӧсъяс ӧтыдждаӧсь.
Эскӧдӧм. Серпас серти, ∠AOB да ∠BOC орччаӧсь, ∠BOC да ∠COD орччаӧсь. Та вӧсна ∠AOB + ∠BOC = 180°, ∠BOC + ∠COD = 180°. Сідзкӧ, ∠AOB = 180° – ∠BOC = ∠COD.

Куимсэрӧгъяс

куимпельӧса, куимсэрӧг — треугольник

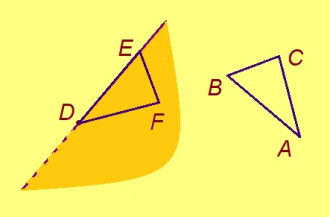
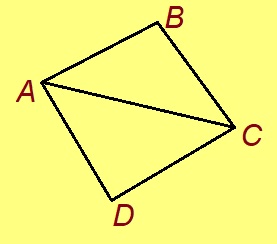
Куимпельӧсаӧн либӧ куимсэрӧгӧн шусьӧ куим чутысь (кодъяс оз куйлыны ӧти веськыд визь вылын) да найӧс йитан вундӧгъясысь тэчӧм мыгӧр. Индӧм куим чутсӧ куимсэрӧгын шуам йывъяснас, а вундӧгъяссӧ — доръяснас.

ABC куимсэрӧгын AB да AС визьньӧвъяс костын куйлысь пельӧс шусьӧ A йывбердса пельӧсӧн.

Ӧткодь куимсэрӧгъяс

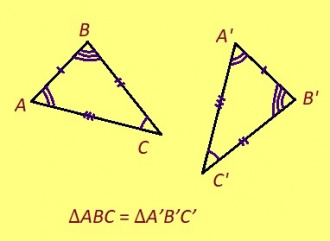
ӧткодь куимсэрӧгъяс – равные треугольники

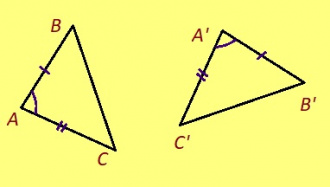
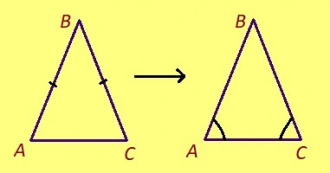
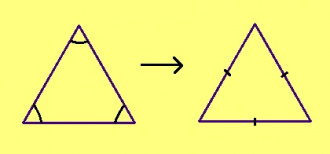
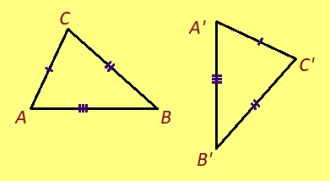
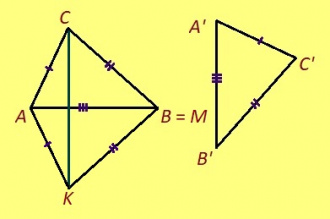
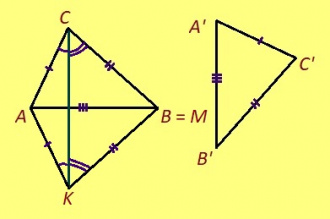
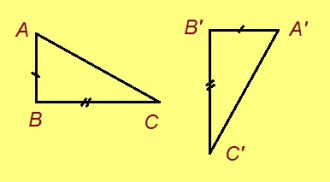
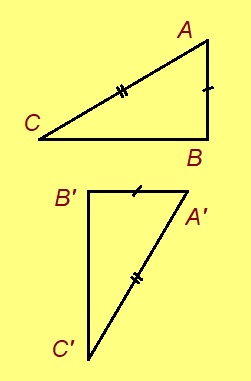
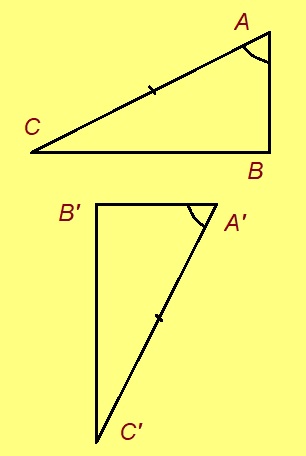
ABC да A’B’C’ куимсэрӧгъяс ӧткодьӧсь, налӧн кӧ ӧта-мӧдыслы лӧсялана пельӧсъяс ӧтыдждаӧсь, а ӧта-мӧдыслы лӧсялана доръясыс ӧткузяӧсь: ∠A = ∠A’, ∠B = ∠B’, ∠C = ∠C’, AB = A’B’, AC = A’C’, BC = B’C’.

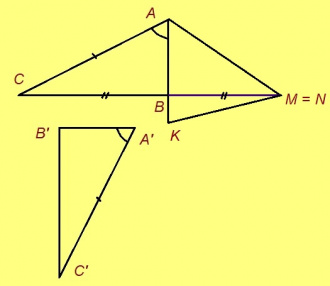
Гижтам визьньӧв. Нюжӧдам кӧ сійӧс, лоӧ веськыд визь, коді юклӧ тшӧтшкӧссӧ кык джынйӧ. Бӧръям тайӧ тшӧтшкӧсджынъяс письыс ӧтиӧс. Сэсся гижтам ABC куимсэрӧг да бӧръям сылысь дорсӧ (шуам, AB вундӧгсӧ), а тайӧ вундӧгыслысь пасъям ӧти помсӧ (шуам, A).

Аксиома. Бӧрйӧм тшӧтшкӧсджынйӧ позьӧ пуктыны ABC-кӧд ӧткодь DEF куимсэрӧг сэтшӧм ногӧн, медым DE вундӧг куйліс индӧм визьньӧвйын да D помыс ӧтлаасис визьньӧвйыслӧн воддза чуткӧд.

Ӧткодь куимсэрӧгъяслӧн медводдза тӧдмӧг

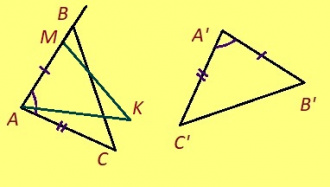
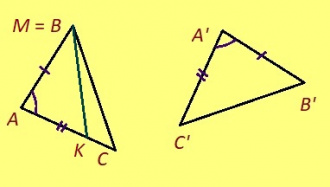
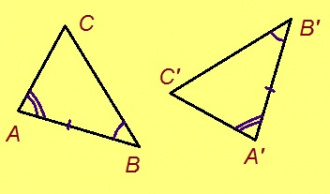
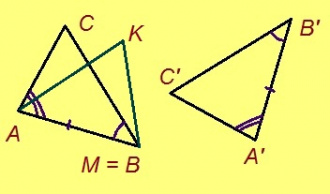
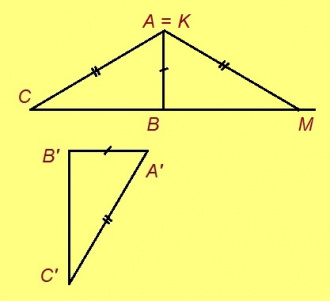
Теорема. Кор ABC да A’B’C’ – куимсэрӧгъяс, AB = A’B’, AC = A’C’, ∠A = ∠A’, сэки ∆ABC = ∆A’B’C’.

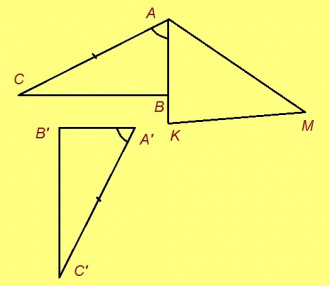
Эскӧдӧм. Аксиомаысь петӧ: позьӧ гижтыны сэтшӧм AMK куимсэрӧг, кӧні: 1) ∆AMK = ∆A’B’C’, 2) AM куйлӧ AB визьньӧвйын, 3) AMK да ABC куйлӧны AB веськыд визь серти ӧти тшӧтшкӧсджынйын.

Кык куимсэрӧгыс (тані ∆AMK да ∆A’B’C’) кӧ ӧткодьӧсь, сэки и налӧн лӧсялана доръясыс да пельӧсъясыс тшӧтш ӧткодьӧсь: AM = A’B’, AK = A’C’, ∠B’A’C’ = ∠MAK. Сідзкӧ:

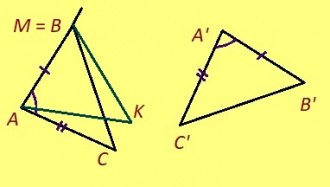
1) AB = A’B’ = AM, сійӧ и M = B;

2) ∠BAC = ∠B’A’C’ = ∠BAK, та вӧсна AK да AC визьньӧвъяс тшӧтш лӧсялӧны;

3) AC = A’C’ = AK, сійӧн и K = C.

Кык чут пыр вермӧ мунны сӧмын ӧти веськыд визь. Сідзкӧ, AMK да ABC куимсэрӧгъяс ӧта-мӧдкӧд лӧсялӧны. Та вӧсна ∆ABC = ∆A’B’C’.

Ӧткодь берда да ӧткодь доръяса куимсэрӧгъяс

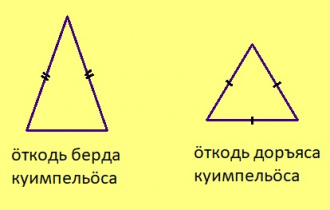
ӧткодь берда куимсэрӧг – равнобедренный треугольник
ӧткодь доръяса куимсэрӧг – равносторонний треугольник
боквыв доръяс – боковые стороны
подув – основание

• Куимсэрӧгын кӧ кык дорыс ӧтыдждаӧсь, шуам сійӧс ӧткодь берда куимсэрӧгӧн.
• Куимсэрӧгын кӧ куимнан дорыс ӧтыдждаӧсь, шуам сійӧс ӧткодь доръяса куимсэрӧгӧн.

Пасйӧд. Ӧткодь берда куимсэрӧгын коймӧд дорыс вермӧ торъявны кык ӧткодь дорсьыс, а вермӧ лоны и на кузьта жӧ. Сэки татшӧм ӧткодь берда куимсэрӧгыс лоӧ тшӧтш ӧткодь доръясаӧн. Сідзкӧ, ӧткодь доръяса куимсэрӧг лоӧ тшӧтш ӧткодь бердаӧн, сылӧн быд кык дорыс ӧтыдждаӧсь да.

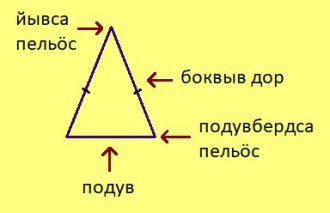
• Ӧткодь берда куимсэрӧгын ӧткодь доръяссӧ шуам боквыв доръясӧн, а коймӧд дорсӧ — подулӧн.
• Подувлы паныд куйлысь пельӧссӧ шуам йывса пельӧсӧн, а боквыв дорлы паныд куйлысь пельӧссӧ — подувбердса пельӧсӧн.

Теорема. Ӧткодь берда куимсэрӧгын подувбердса пельӧсъяс ӧтыдждаӧсь.

Эскӧдӧм. Мед ABC – ӧткодь берда куимсэрӧг, AB = BC. Лыддям куимсэрӧгыслысь йывъяссӧ ӧтарлань да мӧдарлань: ABC да CBA. Пуктам ∆ABC да ∆CBA орччӧн. Казялам: AB = BC, CB = BA, а на костса B пельӧс ӧтувъя. Сідзкӧ, ӧткодьлунсӧ медводдза тӧдмӧг серти, ∆ABC = ∆CBA. А та вӧсна и ∠BAC = ∠BCA.

☼ ☼ ☼

Ӧткодь доръяса куимсэрӧглысь куимнан дорсӧ позьӧ шуны кӧть подулӧн, кӧть боквыв дорӧн, а куимнан пельӧссӧ — кӧть подувбердса, кӧть йывса пельӧсӧн.

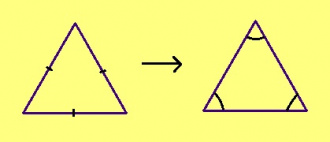
Теорема. Ӧткодь доръяса куимсэрӧгын куимнан пельӧсыс ӧтыджда.

Эскӧдӧм. Мед ABC – ӧткодь доръяса куимсэрӧг. Лыддям кӧ AC дорсӧ подулӧн, сэки ∠BAC = ∠BCA, найӧ подувбердса пельӧсъяс да; BC дорсӧ сідзжӧ позьӧ лыддьыны подулӧн, сэки подувбердса пельӧсъясӧн лоӧны ∠ACB да ∠ABC, сідзкӧ найӧ тшӧтш ӧткодьӧсь. Та дырйи ∠BCA да ∠ACB — ӧти сійӧ жӧ пельӧс (видзӧд серпассӧ). Кык ӧткодьлунсьыс (∠BAC = ∠BCA да ∠BCA = ∠ABC) артмӧ: ∠BAC = ∠BCA = ∠ABC.

Ӧткодь куимсэрӧгъяслӧн мӧд тӧдмӧг

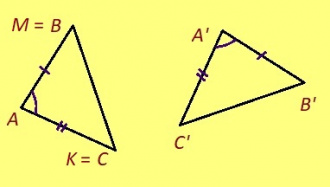
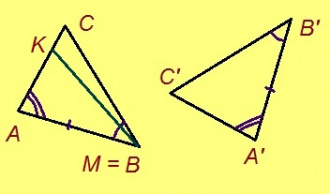
Теорема. Кор ABC да A’B’C’ – куимсэрӧгъяс, AB = A’B’, ∠A = ∠A’, ∠B = ∠B’, сэки ∆ABC = ∆A’B’C’.

Эскӧдӧм. Аксиомаысь петӧ: позьӧ гижтыны сэтшӧм AMK куимсэрӧг, кӧні: 1) ∆AMK = ∆A’B’C’, 2) AM куйлӧ AB визьньӧвйын, 3) AMK да ABC куйлӧны AB веськыд визь серти ӧти тшӧтшкӧсджынйын.

Кык куимсэрӧгыс (тані ∆AMK да ∆A’B’C’) кӧ ӧткодьӧсь, сэки и налӧн лӧсялана доръясыс да пельӧсъясыс тшӧтш ӧткодьӧсь: AM = A’B’, ∠B’A’C’ = ∠MAK, ∠A’B’C’ = ∠AMK. Сідзкӧ:

1) AB = A’B’ = AM, сійӧн и M = B;

2) ∠BAC = ∠B’A’C’ = ∠BAK, та вӧсна AK да AC визьньӧвъяс тшӧтш лӧсялӧны;

3) ∠ABC = ∠A’B’C’ = ∠ABK, та вӧсна BK да BC визьньӧвъяс лӧсялӧны жӧ.

Кык торъялана веськыд визь вермӧ вомӧнасьны сӧмын ӧти чутын. Сідзкӧ, миян K да C ӧти и сійӧ жӧ чут. Вылынджык аддзим: M да B тшӧтш ӧти чут. Со и петӧ, мый AMK да ABC куимсэрӧгъяс лӧсялӧны. А казьтыштам кӧ, мый ∆AMK да ∆A’B’C’ ӧткодьӧсь, сэки и воам кывкӧртӧдӧ: ∆ABC = ∆A’B’C’.

☼ ☼ ☼

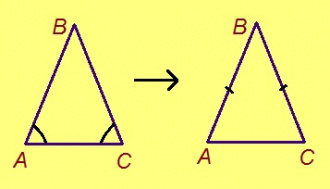
Теорема. Куимсэрӧгыс лоӧ ӧткодь бердаӧн, сыын кӧ эм кык ӧтыджда пельӧс.

Эскӧдӧм. Мед ABC – куимсэрӧг, ∠A = ∠C. Лыддям куимсэрӧгыслысь йывъяссӧ ӧтарлань да мӧдарлань: ABC да CBA. Пуктам ∆ABC да ∆CBA орччӧн. Казялам: ∠A = ∠C, ∠C = ∠A, а на костса AC дорыс ӧтувъя. Сідзкӧ, ӧткодьлунсӧ мӧд тӧдмӧг серти, ∆ABC = ∆CBA. А та вӧсна и AB = BC.

☼ ☼ ☼

Кывкӧртӧд 1. Куимсэрӧгын кӧ эм кык ӧтыджда пельӧс, татшӧм куимсэрӧгыс быть лоӧ ӧткодь бердаӧн; и мӧдарӧ, куимсэрӧгыс кӧ ӧткодь берда, сыын быть эм кык ӧтыджда пельӧс. (Дженьдӧдӧм могысь шуӧны тадзи: куимсэрӧг ӧткодь берда сэк да сӧмын сэк, кор сыын эм кык ӧтыджда пельӧс.)

Кывкӧртӧд 2. Куимсэрӧгын кӧ куимнан пельӧсыс ӧтыдждаӧсь, татшӧм куимсэрӧгыс быть лоӧ ӧткодь доръясаӧн; и мӧдарӧ, куимсэрӧгыс кӧ ӧткодь доръяса, сылӧн куимнан пельӧсыс ӧтыдждаӧсь. (Дженьдӧдӧм могысь шуӧны тадзи: куимсэрӧг ӧткодь доръяса сэк да сӧмын сэк, кор сыын куимнан пельӧсыс ӧтыдждаӧсь.)

Биссектриса, медиана да судта

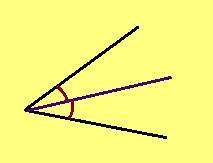
• Биссектрисаӧн шуӧны визьньӧв, коді петӧ пельӧс йылысь да юклӧ тайӧ пельӧссӧ шӧрипӧв.

• Куимсэрӧгын биссектрисаӧн шуӧны вундӧг, коді юклӧ сылысь ӧти пельӧссӧ шӧрипӧв да йитӧ тайӧ пельӧс йывсӧ паныда дор вылын куйлысь чуткӧд.

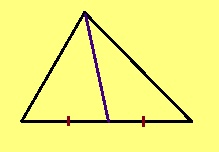
• Куимсэрӧгын медианаӧн шуӧны вундӧг, коді йитӧ сылысь ӧти йывсӧ паныда дорвывса шӧр чуткӧд.

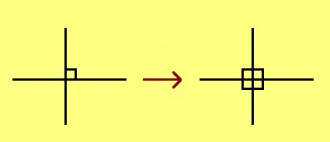
Теорема. Кык веськыд визь кӧ вомӧнасьӧны да та дырйи артмӧм нёль пельӧсысь ӧтиыс кӧ лоӧ бур, сэки мукӧд куим пельӧсыс тшӧтш бурӧсь.

Эскӧдӧм. Тайӧ куим пельӧс пӧвстысь ӧтиыс куйлӧ 90°‐а пельӧскӧд вертикаль ногӧн, та вӧсна сійӧ лоӧ тшӧтш бур (вертикаль пельӧсъяс ӧткодьӧсь да). Мӧд кыкыс 90°‐а пельӧскӧд орччаӧсь, та вӧсна и найӧ бурӧсь (кыдзи ми тӧдам нин).

• Веськыд визь шусьӧ перпендикулярӧн мӧд веськыд визьлы, найӧ кӧ артмӧдӧны бур пельӧс.

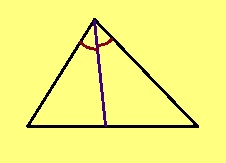
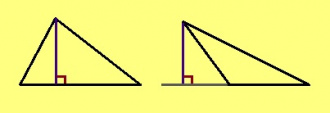
• Куимсэрӧгын судтаӧн шуӧны вундӧг, коді йитӧ сылысь ӧти йывсӧ паныда дор визь вылын куйлысь чуткӧд да лоӧ тайӧ дорыслы перпендикулярӧн.

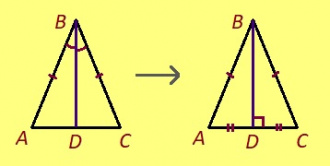
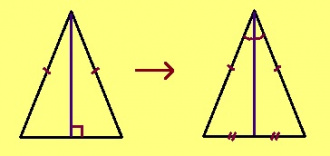
Теорема. Ӧткодь берда куимсэрӧгын йывса пельӧсса биссектрисаыс лоӧ ӧттшӧтш медианаӧн да судтанас.

Эскӧдӧм. Мед ABC – куимсэрӧг, кӧні AB = BC, а BD – биссектрисаыс, коді юклӧ ABC-сӧ кык пельӧ: ∆ABD да ∆CBD. Казялам: AB = CB, ∠ABD = ∠CBD, а BD – налӧн ӧтувъя дор. Ӧткодьлунсӧ медводдза тӧдмӧг серти, ∆ABD = ∆CBD. Таысь петӧ кык тор:

1. AD = DC, а сідзкӧ, BD — медиана;
2. ∠BDA = ∠BDC; серпасысь позьӧ аддзыны, мый тайӧ ӧткодь пельӧсъясыс орччаӧсь. Кыдзи ми тӧдам, орчча пельӧсъяслӧн суммаыс 180°, та вӧсна ∠BDA = 90° да ∠BDC = 90°, а сідзкӧ, BD — судта.

Ӧткодь куимсэрӧгъяслӧн коймӧд тӧдмӧг

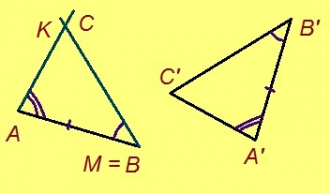
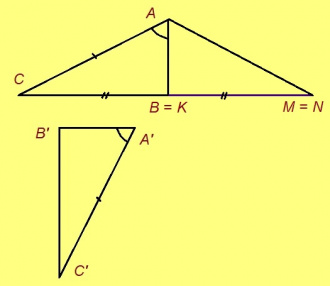
Теорема. Кор ABC да A’B’C’ – куимсэрӧгъяс, кӧні AB = A’B’, BC = B’C’, AC = A’C’, сэки ∆ABC = ∆A’B’C’.

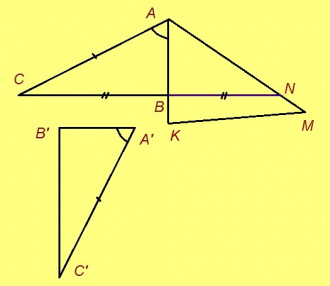
Эскӧдӧм. Аксиомаысь петӧ: позьӧ гижтыны сэтшӧм AMK куимсэрӧг, кӧні: 1) ∆AMK = ∆A’B’C’; 2) AM куйлӧ AB визьньӧвйын; 3) K да C чутъяс куйлӧны торъя тшӧтшкӧсджынъясын AB веськыд визь серти.

(колӧ серпас)

AB = A’B’ = AM, та вӧсна M = B.

AC = A’C’ = AK; сідзкӧ, AC да AK – боквыв доръяс ӧткодь берда CAK куимсэрӧгын. Та вӧсна ∠AKC = ∠ACK. Сэтшӧм жӧ ногӧн артмӧдам: ∠BKC = ∠BCK.

Сідзкӧ, ∠ACB = ∠ACK + ∠BCK = ∠AKC + ∠BKC = ∠AKB. Таысь кындзи, AC = AK, BC = BK. Сы вӧсна ABC да ABK куимсэрӧгъяс ӧткодьӧсь медводдза тӧдмӧг серти да ∆A’B’C’ = ∆ABK = ∆ABC.

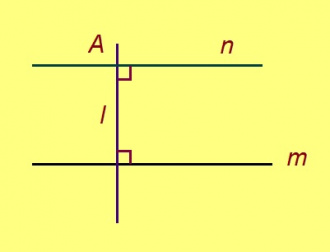
Веськыд визьлань ортсы чут пыр гижтӧм перпендикуляр

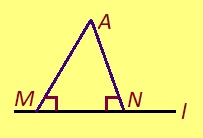
Теорема. Веськыд визьысь ортсыын куйлысь чут пыр оз позь гижтыны сы дорӧ кык торъялана перпендикуляр.

Эскӧдӧм (паныдсянь). Мед A чут лоӧ l веськыд визьысь ортсыын, а AM да AN – тайӧ визь дорас кык торъялана перпендикуляр, кодъяс вомӧналӧны l-сӧ M да N чутъясын. Та дырйи M да N – кык торъялана чут.

Аксиомаысь петӧ: позьӧ гижтыны сэтшӧм MBN куимсэрӧг, кӧні: 1) ∆MBN = ∆MAN, 2) A да B чутъяс куйлӧны l веськыд визь серти торъя тшӧтшкӧсджынъясын.

Миян артмӧ: ∠AMN = ∠BMN = 90°; та вӧсна ∠AMB = 180° да M чут куйлӧ AB веськыд визь вылын. Сэтшӧм жӧ ногӧн артмӧдам: N чут куйлӧ AB веськыд визь вылын. AB да l веськыдъяс вомӧнасьӧны сӧмын ӧти чутын. Сідзкӧ, M = N, а тайӧ оз лӧсяв миян воддза шуӧмкӧд, код серти M да N – кык торъялана чут.

Теорема. Ӧткодь берда куимсэрӧгын йывса пельӧсса судта лоӧ ӧттшӧтш биссектрисаӧн да медианаӧн.

Эскӧдӧм (паныдсянь). Мед судтаыс оз ло биссектрисаӧн. Гижтам йывса пельӧслысь биссектрисасӧ. Кыдзи ми тӧдам нин, ӧткодь берда куимсэрӧгын йывса пельӧслӧн биссектрисаыс ӧттшӧтш лоӧ сылы судтаӧн. Сідзкӧ, йывса пельӧсысь позьӧ гижтыны подувлы кык торъялана перпендикуляр, а тайӧ оз лӧсяв воддза теоремакӧд.

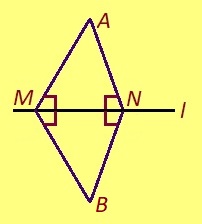
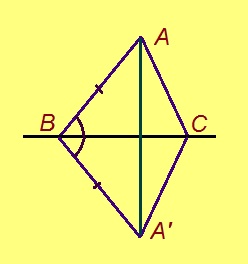
Теорема. Веськыд визь дорӧ сыысь ортсыын куйлысь чут пырыс позьӧ гижтыны перпендикуляр.

Эскӧдӧм. Мед A чут куйлӧ l веськыд визьысь ортсыын, B да C чутъяс лоӧны l вылын. Аксиомаысь петӧ: позьӧ гижтыны сэтшӧм BA’C куимсэрӧг, кӧні: 1) ∆BA’C = ∆BAC, 2) A да A’ чутъяс куйлӧны l веськыд визь серти торъя тшӧтшкӧсджынъясын. Сідзкӧ, ABA’ куимсэрӧгын AB = A’B, BC визьньӧв – ∠ABA’-лӧн биссектриса. Кыдзи ми тӧдам нин, ӧткодь берда куимсэрӧгын йывса пельӧслӧн биссектрисаыс ӧттшӧтш лоӧ сылы судтаӧн. Сідзкӧ, AA’ лоӧ l-лы перпендикулярӧн.

Ортсыса пельӧс

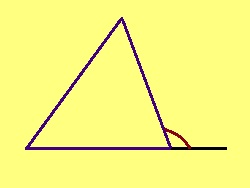
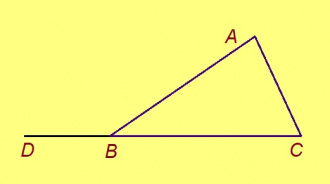
Куимсэрӧглысь став видлалӧм сикас пельӧсъяссӧ позьӧ шуны тшӧтш пытшкӧс пельӧсъясӧн. Куимсэрӧг бердын куимнан пытшкӧс пельӧскӧд орччӧн куйлӧны ортсы пельӧсъяс. Мӧд ногӧн шуны, куимсэрӧглӧн ортсы пельӧсӧн шусьӧ быд пытшкӧс пельӧскӧд орчча пельӧс.

Теорема. Ортсыса пельӧс ыджыдджык куимсэрӧгса кыкнан пельӧсысь, коді сыкӧд абу орччӧн.

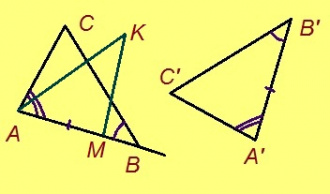
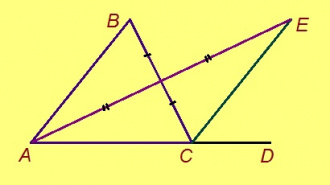
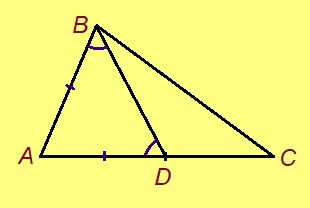
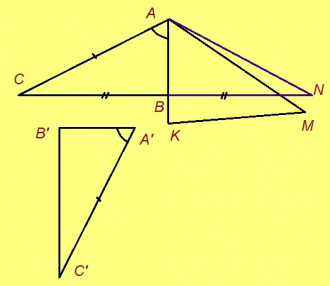
Эскӧдӧм. Мед ABC — куимсэрӧг, ∠BCD — сылӧн ортсы пельӧс, коді куйлӧ ∠BCA-кӧд орччӧн; та дырйи C чут куйлӧ A да D костын. Петкӧдлам: ∠ABC < ∠BCD.

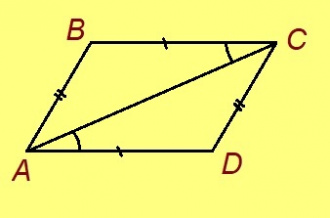
Та могысь гижтам ∠BCD пельӧс доръяс костӧд сэтшӧм CE визьньӧв, медым ∠ABC = ∠BCE. Кытысь лоӧ E чутыс? BC вундӧг шӧрын куйлысь чут пыр (пасъям сійӧс O) гижтам AO визьньӧв. Тайӧ визьньӧв вылас пасъям E чут, коді куйлӧ O чутсянь сы ылнаын жӧ, кыдзи и A чут. Миян артмӧ: 1) OC = OB; 2) AO = OE; 3) ∠AOB = ∠EOC кыдзи вертикаль пельӧсъяс. Сідзкӧ ∆AOB = ∆EOC медводдза тӧдмӧг серти. Та вӧсна ∠ABC = ∠BCE, кыдзи ӧткодь куимсэрӧгъясын лӧсялана пельӧсъяс.

O, B да E чутъяс куйлӧны ӧти тшӧтшкӧсджынйын AD веськыд визь серти. Миян артмӧ: 1) ∠BCD = 180° – ∠BCA (кыдз орчча); 2) ВС да AE вундӧгъяс вомӧнасьӧны, мӧд ног шуны, CB визьньӧв мунӧ ∠ACE пельӧс доръяс костӧд. Сідзкӧ ∠ACE = ∠BCE + ∠BCA. 3) ∠ACE < 180°, та вӧсна ∠ACE-ысь кӧ чинтам ∠BCA да 180°-ысь сійӧ жӧ ∠BCA чинтам, медводдза чинтасыс лоас этшаджык мӧд чинтассьыс (формулаӧн кӧ пасъям, ∠ACE – ∠BCA < 180° – ∠BCA).

Ӧтувтам кӧ став артмӧм формула, лоас:

∠ABC = ∠BCE;

∠BCE = ∠ACE – ∠BCA;

∠ACE – ∠BCA < 180° – ∠BCA;

180° – ∠BCA = ∠BCD.

Сідзкӧ ∠ABC < ∠BCD.

Сэтшӧм жӧ ногӧн артмӧдам, мый ∠BAC < ∠BCD.

Куимсэрӧглысь доръяс да пельӧсъяс ӧтластитӧм

Теорема. Куимсэрӧгын ыджыдджык дорлы паныд куйлӧ ыджыдджык пельӧс.

Эскӧдӧм. Мед ABC куимсэрӧгын AC > AB. Петкӧдлам: ∠ABC > ∠ACB. Пасъям AC вундӧг вылын сэтшӧм D чут, медым AD = AB. Сідзкӧ, ∠ABD = ∠BDA, ӧд найӧ ӧткодь берда куимсэрӧгын подувбердса пельӧсъяс.

BD вундӧг юкӧ ∆ABC-сӧ кык пельӧ; сы пытшкын ӧні эм кык куимсэрӧг: ∆ABD да ∆BCD. ∠BDA лоӧ ∆BCD куимсэрӧглы ортсыса пельӧс. Кыдзи ми тӧдам нин, ортсыса пельӧс век ыджыдджык пытшкӧсса пельӧсысь, коді сыкӧд абу орчча. Сідзкӧ ∠BDA > ∠BCD. Ӧтувтам кӧ став артмӧм формула, лоас:

∠ABC > ∠ABD,

∠ABD = ∠BDA,

∠BDA > ∠BCD,

∠BCD = ∠ACB.

Сідзкӧ, ∠ABC > ∠ACB.

Теорема. Куимсэрӧгын ыджыдджык пельӧслы паныд куйлӧ ыджыдджык дор.

(татчӧ колӧ серпас)

Эскӧдӧм. Мед ABC куимсэрӧгын ∠ABC > ∠ACB. Петкӧдлам: AC > AB.

Тайӧ кӧ абу сідз, либӧ AC = AB, либӧ AC < AB. Кыдзи ми тӧдам нин, кор AC = AB, сэки ∠ABC = ∠ACB; кор AC < AB, сэки ∠ABC < ∠ACB. Тайӧ оз лӧсяв ∠ABC > ∠ACB ӧткодьтӧмлункӧд.

☼ ☼ ☼

Сідзкӧ, куимсэрӧгын ӧти дор кузьджык мӧд дорсьыс сэк да сӧмын сэк, кор медводдза дорыслы паныд куйлан пельӧс ыджыдджык мӧд дорыслы паныд куйлан пельӧсысь.

Ёсь пельӧса, бур (веськыд) пельӧса да ныж пельӧса куимсэрӧгъяс

ёсь пельӧса куимсэрӧг — остроугольный треугольник
бур (веськыд) пельӧса куимсэрӧг — прямоугольный треугольник
ныж пельӧса куимсэрӧг — тупоугольный треугольник

Куимсэрӧг шусьӧ ёсь пельӧсаӧн, сыын кӧ куимнан пельӧсыс ёсь.

Куимсэрӧг шусьӧ бур (веськыд) пельӧсаӧн, сыын кӧ ӧти пельӧсыс бур (веськыд).

Куимсэрӧг шусьӧ ныж пельӧсаӧн, сыын кӧ ӧти пельӧсыс ныж.

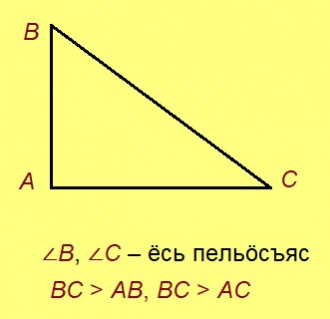
Теорема. 1) Бур пельӧса куимсэрӧгын гипотенузабердса пельӧсъяс ёсьӧсь. 2) Гипотенуза кузьджык катетысь.

Эскӧдӧм. 1) Бур пельӧскӧд орчча пельӧс тшӧтш бур; теорема серти, сійӧ ыджыдджык гипотенузабердса пельӧсысь. 2) Бур (веськыд) пельӧсыс куимсэрӧгын медыджыд, та вӧсна сылы паныд куйлысь дор медкузь.

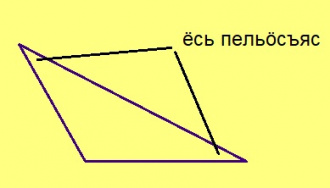
Висьталӧм. Ныж пельӧса куимсэрӧгын эм кык ёсь пельӧс.

Эскӧдӧм. Ӧти пельӧсыс кӧ ныж, сыкӧд орчча пельӧсыс ёсь. Кыдз ми тӧдам нин, ортсыса пельӧс ыджыдджык пытшкӧсса пельӧсысь, коді абу сыкӧд орччӧн. Сідзкӧ куимсэрӧгыслӧн мукӧд пытшкӧсса пельӧсъяс ёсь пельӧсысь ичӧтджыкӧсь; та вӧсна найӧ асьныс ёсьӧсь.

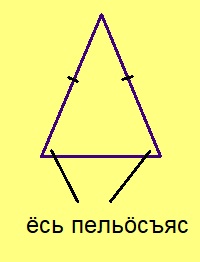
Висьталӧм. Ӧткодь берда куимсэрӧгын подувбердса пельӧсъяс ёсьӧсь.

Эскӧдӧм. Кыдз ми тӧдам нин, 1) ӧткодь берда куимсэрӧгын подувбердса пельӧсъяс ӧтыдждаӧсь, 2) бур пельӧса либӧ ныж пельӧса куимсэрӧгын эм кык ёсь пельӧс. Сідзкӧ, подувбердса пельӧс оз вермы лоны бурӧн ни ныжӧн.

Бур пельӧса ӧткодь куимсэрӧгъяслӧн тӧдмӧг

Кык катет серти.

Теорема. Кор ABC да A’B’C’ — бур пельӧса куимсэрӧгъяс, кӧні AB, BC, A’B’, B’C’ — катетъяс, AB = A’B’, BC = B’C’, сэки ∆ABC = ∆A’B’C’.

Эскӧдӧм. ∠ABC = ∠A’B’C’ = 90°, AB = A’B’, BC = B’C’; сідзкӧ, куимсэрӧгъясыс ӧткодьӧсь медводдза тӧдмӧг серти.

Катет да гипотенуза серти.

Теорема. Кор ABC да A’B’C’ — бур пельӧса куимсэрӧгъяс, кӧні AB да A’B’ — катетъяс, AC да A’C’ — гипотенузаяс, AB = A’B’, AC = A’C’, сэки ∆ABC = ∆A’B’C’.

Эскӧдӧм. Аксиомаысь петӧ: позьӧ гижтыны сэтшӧм KBM куимсэрӧг, кӧні: 1) ∆KBM = ∆A’B’C’, 2) M чут куйлӧ куйлӧ BC визь вылын, B чут куйлӧ C да M чутъяс костын, 3) ∆KBM да ∆ABC куйлӧны BC веськыд визь серти ӧти тшӧтшкӧсджынйын.

Медводдза серпас вылас ылӧсас индӧма, кутшӧм тшӧтшкӧсджынйын куйлӧ K чут. Сэсся ми сьӧрсьӧн-бӧрсьӧн кутам стӧчмӧдны сылысь инсӧ.

Но кыдзи ми тӧдам, ∆KBM = ∆A’B’C’. Таысь петӧ некымынтор:

1) ∠KBM = ∠A’B’C’ = 90°, ∠ABM = 180° − ∠ABC = 90°; сійӧн K чутлы быть куйлыны BA визьньӧв вылын.

2) AB = A’B’, A’B’ = KB; та вӧсна AB = KB да K чутлы быть лӧсявны A-кӧд.

(серпас)

3) AC = A’C’, A’C’ = KM = AM; сійӧн AC = AM.

Миян артмӧ ∆CAM. Сійӧ — ӧткодь берда куимсэрӧг, кӧні AC да AM — боквыв доръяс, AB — судта. Кыдзи ми тӧдам нин, подувлань гижтӧм судта лоӧ биссектрисаӧн. Миян артмӧ: AC = AM, ∠CAB = ∠MAB. Сідзкӧ, ∆ABC = ∆ABM медводдза тӧдмӧг серти. Но ∆ABM = ∆KBM = ∆A’B’C’. Сійӧн ∆ABC = ∆A’B’C’.

Катет да сы бердса ёсь пельӧс серти.

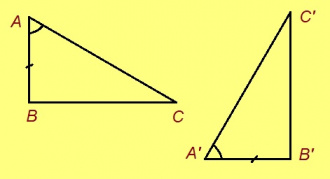
Теорема. Кор ABC да A’B’C’ — бур пельӧса куимсэрӧгъяс, кӧні AB да A’B’ — катетъяс, ∠A да ∠A’ — ёсь пельӧсъяс, AB = A’B’, ∠A = ∠A’, сэки ∆ABC = ∆A’B’C’.

Эскӧдӧм. ∠B = ∠B’ = 90°, AB = A’B’, ∠A = ∠A’; сідзкӧ, куимсэрӧгъясыс ӧткодьӧсь мӧд тӧдмӧг серти.

Катет да сылы паныд куйлысь ёсь пельӧс серти.

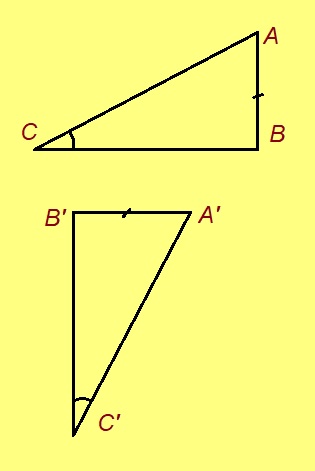
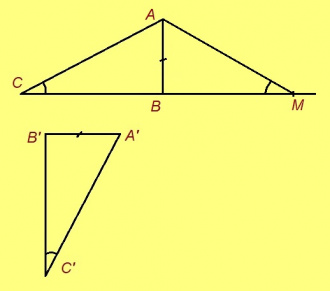
Теорема. Кор ABC да A’B’C’ — бур пельӧса куимсэрӧгъяс, кӧні AB да A’B’ — катетъяс, AB = A’B’, ∠B = ∠B’ = 90°, ∠C = ∠C’, сэки ∆ABC = ∆A’B’C’.

Эскӧдӧм. Аксиомаысь петӧ: позьӧ гижтыны сэтшӧм KBM куимсэрӧг, кӧні: 1) ∆KBM = ∆A’B’C’, 2) M чут куйлӧ куйлӧ BC визь вылын, B чут куйлӧ C да M чутъяс костын, 3) ∆KBM да ∆ABC куйлӧны BC веськыд визь серти ӧти тшӧтшкӧсджынйын.

Татшӧм KBM куимсэрӧгсӧ миян лӧсьӧдлім мӧд теоремасӧ подулалігӧн. Сэки миян артмис: K = A.

Сідзкӧ ∆ABM = ∆A’B’C’. Та вӧсна ∠AMB = ∠A’C’B’. Но ∠A’C’B’ = ∠ACB. Сійӧн ∠AMB = ∠ACB.

Кыдзи ми тӧдам нин, куимсэрӧгын кӧ эм кык ӧткодь пельӧс, тайӧ куимсэрӧгыс ӧткодь берда. Сідзкӧ ACM — ӧткодь берда куимсэрӧг, CM — сылӧн подулыс, AB — сылӧн судтаыс. Татшӧмтор миян бара жӧ артмыліс нин мӧд теоремасӧ подулалігӧн; сыысь ми тӧдан нин, мый ∆ABC = ∆ABM = ∆A’B’C’.

Гипотенуза да ёсь пельӧс серти.

Теорема. Кор ABC да A’B’C’ — бур пельӧса куимсэрӧгъяс, кӧні AC да A’C’ — гипотенузаяс, AC = A’C’, ∠A = ∠A’, сэки ∆ABC = ∆A’B’C’.

Эскӧдӧм. Аксиомаысь петӧ: позьӧ гижтыны сэтшӧм AKM куимсэрӧг, кӧні: 1) ∆AKM = ∆A’B’C’, 2) AK куйлӧ AB визьньӧвйын, 3) ∆AKM да ∆ABC куйлӧны AB веськыд визь серти торъя тшӧтшкӧсджынъясын.

Медводдза серпас вылас ылӧсас индӧма, кутшӧм визьньӧв вылын куйлӧ K чут да кутшӧм тшӧтшкӧсджынйын куйлӧ M чут. Сэсся ми сьӧрсьӧн-бӧрсьӧн кутам стӧчмӧдны налысь инсӧ.

Пуктам N чут CB визьньӧв вылӧ тадзи, медым BC = BN. Сэки ∆ABC = ∆ABN кык катет серти.

Миян артмӧ:

1) ∠BAN = ∠BAC;

2) ∠BAC = ∠B’A’C’;

3) ∠B’A’C’ = ∠KAM = ∠BAM.

Сідзкӧ ∠BAN = ∠BAM; та вӧсна N чут куйлӧ AM визьньӧв вылын. Пасъям тайӧс выль серпас вылын, сэсся водзӧ кутам стӧчмӧдны K‐лысь да M‐лысь инсӧ.

∆ABC = ∆ABN, та вӧсна AC = AN; но AC = A’C’ да A’C’ = AM. Сідзкӧ AM = AN, кытысь M = N. Вӧчам выль серпас, кӧні M = N; колис сӧмын стӧчмӧдны K чутлысь инсӧ.

∠AKM = ∠A’B’C’ = 90°, ∠ABM = ∠ABC = 90°. Сійӧн MB да MK лоӧны AB‐лы перпендикуляръясӧн. Кыдзи ми тӧдам нин, ӧти чутысь позьӧ гижтыны сӧмын ӧти перпендикуляр. Сідзкӧ, K = B.

Миян артмӧ:

1) ∆ABC = ∆ABM;

2) ∆ABM = ∆A’B’C’.

Та вӧсна ∆ABC = ∆A’B’C’.

Куимсэрӧг ӧткодьтӧмлун

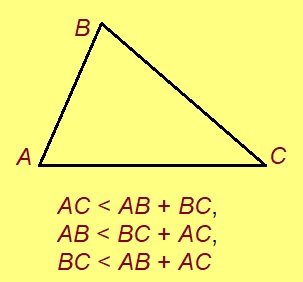
Теорема. Куимсэрӧгын кык дорыслӧн ӧтувъя кузьта век лоӧ ыджыдджык коймӧд дор кузьтасьыс.

Эскӧдӧм. Шуам, ABC куимсэрӧгын AC дор лоӧ медкузьӧн. Сідзкӧ AC вундӧгас позьӧ пуктыны D чут, медым AB = AD. Миян артмӧ: ∆DAB — ӧткодь берда куимсэрӧг, DB — сылӧн подулыс, ∠ADB да ∠ABD — сылӧн подувбердса пельӧсъяс.

Кыдзи ми тӧдам нин, подувбердса пельӧсыд век лоӧ ёсь. Сідзкӧ, ∠ADB тшӧтш ёсь. Ёсь пельӧскӧд орчча пельӧс век лоӧ ныж. Сійӧн ∠BDC — ныж пельӧс. Миян артмӧ: BDC куимсэрӧгын ∠BDC медыджыд. Кыдзи ми тӧдам нин, медыджыд пельӧслы паныд куйлӧ медкузь дор. Сы понда BC > DC.

Миян артмӧ:

• AC = AD + DC;
• AD = AB (сійӧн вылысджык формула позьӧ гижны: AC = AB + DC);
• DC < BC.

Сідзкӧ, AC < AB + BC.

Параллель (ӧтнырвизя) веськыд визьяс

Кык веськыд визь шусьӧны параллельясӧн, найӧ кӧ оз вомӧнасьны.

Кор a да b веськыд визьяс куйлӧны параллель ногӧн, гижӧны a ∥ b.

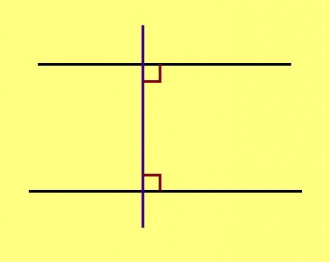
Теорема. Кык торъялана веськыд визь кӧ лоӧны перпендикуляръясӧн коймӧд веськыд визьлы, найӧ параллель ногаӧсь.

Эскӧдӧм (паныдсянь). Тайӧ кык веськыд визь кӧ вомӧнасисны, найӧ вомӧнасянінысь позис эськӧ гижтыны коймӧд веськыд визьлань кык торъялана перпендикуляр. Но, кыдзи ми тӧдам нин, тайӧс вӧчны он вермы.

(татчӧ колӧ серпас)

Теорема. Чутыс кӧ оз куйлы веськыд визь вылын, сэтшӧм чут пыр позьӧ гижтыны тайӧ веськыд визьлы параллель.

Эскӧдӧм. Мед миян эм m веськыд визь да A чут, коді оз куйлы сы вылын. Гижтам A чутысь m-лань перпендикуляр (пасъям сійӧс l). Сэсся A чут пыр гижтам l-лы перпендикуляр (пасъям сійӧс n). Миян артмӧ: l лоӧ перпендикулярӧн m-лы да n-лы. Сідзкӧ, m да n параллельяс (воддза теорема серти).

Параллель визьяслӧн тӧдмӧг

пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс – внутренние накрест лежащие углы
ортсыса ӧтар-мӧдар куйлысь пельӧсъяс – внешние накрест лежащие углы
пытшкӧсса ӧтарбокса пельӧсъяс – внутренние односторонние углы
ортсыса ӧтарбокса пельӧсъяс – внешние односторонние углы
весьтаса пельӧсъяс – соответственные углы

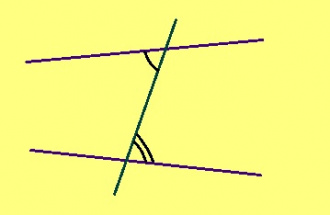
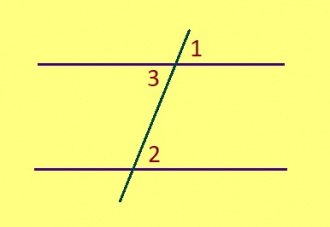
Гижтам кык веськыд визь да нӧшта ӧти визь, коді найӧс вомӧналӧ. Тайӧ вомӧналысь визь серти позьӧ пасйыны татшӧм пельӧсъяс (петкӧдлӧма серпас вылын):

• пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс,

• ортсыса ӧтар-мӧдар куйлысь пельӧсъяс,

• пытшкӧсса ӧтарбокса пельӧсъяс,

• ортсыса ӧтарбокса пельӧсъяс,

• весьтаса пельӧсъяс.

(петкӧдлыны серпас вылын став вариант − 2, 2, 2, 2, 4)

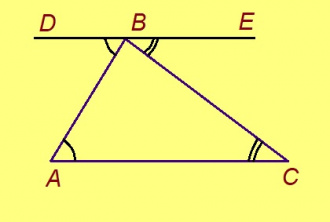
Теорема. Эм кык веськыд визь, найӧс вомӧналӧ нӧшта ӧти визь. Вомӧналысь визь серти пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс кӧ ӧтыдждаӧсь, веськыд визьясыс параллель ногаӧсь.

Эскӧдӧм. Эм кык веськыд визь: AC да BD; найӧс вомӧналӧ нӧшта ӧти визь: AB; та дырйи ∠ABD = ∠BAC. Пасъям AB вундӧглысь шӧрчутсӧ M шыпасӧн. Гижтам M чут пыр AC веськыд визьлань MP перпендикуляр. Чут, кӧні сійӧ вомӧнасьӧ BD-кӧд, пасъям Q шыпасӧн. ∠AMP да ∠BMQ — вертикаль пельӧсъяс, та вӧсна найӧ ӧтыдждаӧсь. Сідзкӧ, ∆AMP = ∆BMQ мӧд тӧдмӧг серти. Сэк и ∠BQM = ∠APM. MP лоӧ AC‐лы перпендикуляр, сійӧн ∠APM = 90°; сідзкӧ и ∠BQM = 90°. Миян артмӧ: BQ да AP веськыд визьяс лоӧны PQ веськыд визьлы перпендикуляръясӧн. Сідзкӧ, найӧ куйлӧны мӧда-мӧдлы параллель ногӧн водзджык подулалӧм теорема серти.

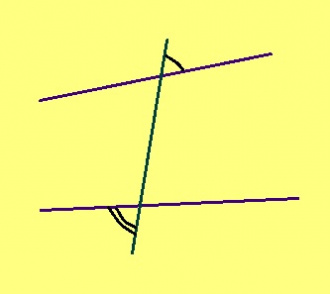
Теорема. Эм кык веськыд визь, найӧс вомӧналӧ нӧшта ӧти визь. Вомӧналысь визь серти ортсыса ӧтар-мӧдар куйлысь пельӧсъяс кӧ ӧтыдждаӧсь, веськыд визьясыс параллель ногаӧсь.

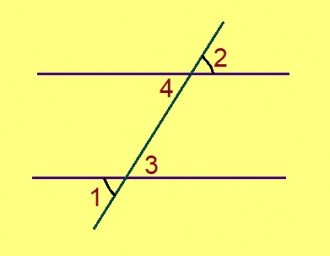
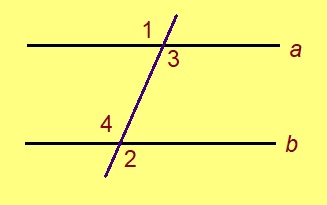
Эскӧдӧм. Мед ∠1, ∠2 – ортсыса ӧтар-мӧдар куйлысь пельӧсъяс, ∠1 = ∠2.

∠1 = ∠3, ∠2 = ∠4 кыдзи вертикаль пельӧсъяс. Сідзкӧ, ∠3 = ∠4. Тайӧ пельӧсъясыс – пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс. Воддза теорема серти, веськыд визьясыс параллель ногаӧсь.

Теорема. Эм кык веськыд визь, найӧс вомӧналӧ нӧшта ӧти визь. Вомӧналысь визь серти ӧтарбокса пытшкӧсса либӧ ортсыса пельӧсъяслӧн суммаыс кӧ 180°, веськыд визьясыс параллель ногаӧсь.

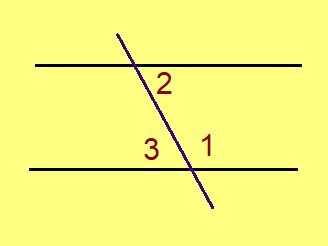
Эскӧдӧм. Мед ∠1, ∠2 – пытшкӧсса ӧтарбокса пельӧсъяс, ∠1 + ∠2 = 180°.

∠2 да ∠3 орччаӧсь, та вӧсна ∠2 + ∠3 = 180°. Сідзкӧ, ∠1 = ∠3. ∠1 да ∠3 пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс; водзджык подулалӧм теорема серти та дырйи веськыд визьясыс лоӧны параллель ногаӧсь.

Ортсыса ӧтарбокса пельӧсъяслӧн суммаыс кӧ 180° ыджда, теоремасӧ подулалам сэтшӧм жӧ ногӧн.

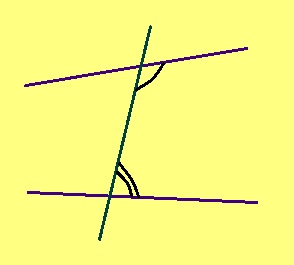
Теорема. Эм кык веськыд визь, найӧс вомӧналӧ нӧшта ӧти визь. Вомӧналысь визь серти весьтаса пельӧсъяс кӧ ӧтыдждаӧсь, веськыд визьясыс параллель ногаӧсь.

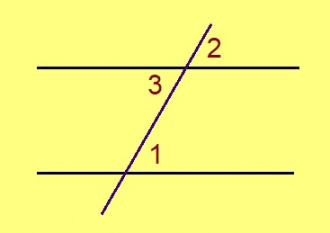
Эскӧдӧм. Мед ∠1, ∠2 – весьтаса пельӧсъяс, ∠1 = ∠2.

∠1 да ∠3 — вертикаль пельӧсъяс, та вӧсна ∠1 = ∠3. Сідзкӧ ∠2 = ∠3. Но ∠2 да ∠3 — пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс. А водзджык подулалӧм теорема серти та дырйи веськыд визьясыс лоӧны параллель ногаӧсь.

Параллель йылысь аксиома

Аксиома. Веськыд визьысь ортсыын куйлысь чут пыр позьӧ гижтыны дзик ӧти параллель.

Теорема. Кык торъялана веськыд визь кӧ лоӧны параллельясӧн коймӧд веськыд визьлы, найӧ лоӧны ӧта-мӧдыслы параллельясӧн.

Эскӧдӧм. Мед a да b веськыд визьяс лоӧны c веськыд визьлы параллельясӧн. Найӧ кӧ вомӧнасьӧны кутшӧмкӧ чутын, тайӧ чут пырыс мунӧ c-лы кык торъялана параллель. Тайӧ оз лӧсяв аксиомакӧд.

Параллель нога веськыд визьяслӧн аслунъяс

Теорема. Кор параллель ногӧн куйлысь кык веськыд визьсӧ вомӧналӧ коймӧд веськыд визь, сэки артмӧм пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс ӧтыдждаӧсь.

Эскӧдӧм. Мед AD да BC параллельяс, AB веськыд визь найӧс вомӧналӧ. Миянлы колӧ петкӧдлыны: ∠DAB = ∠CBA.

(серпас)

Гижтам A чут пыр AE веськыд визь сідзи, медым ∠EAB = ∠CBA. Кыдзи ми тӧдам нин, пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс кӧ ӧтыдждаӧсь, веськыд визьясыс лоӧны параллельясӧн. Сійӧн EA-лы да BC-лы быть лоны параллельясӧн.

Мый эськӧ вӧлі, ∠DAB да ∠CBA кӧ эз вӧвны ӧтыдждаӧсь? Сэки AD да AE вӧліны эськӧ торъялана веськыд визьясӧн, кыдзи петкӧдлӧма серпас вылын.

Та дырйи A чут пыр муніс эськӧ BC-лы торъялана кык параллель: AD да AE, а тайӧ оз лӧсяв аксиомакӧд.

Теорема. Параллель ногӧн куйлысь кык веськыд визьсӧ кӧ вомӧналӧ коймӧд веськыд визь, сысянь ортсыса ӧтар-мӧдар куйлысь пельӧсъяс ӧтыдждаӧсь.

Эскӧдӧм. Гижтам серпас, кӧні ∠1 да ∠2 – ортсыса ӧтар-мӧдар куйлысь пельӧсъяс.

• Та дырйи ∠1 = ∠3, ∠2 = ∠4, ставныс вертикаль пельӧсъяс да сійӧн;
• а ∠3 = ∠4, найӧ пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс да (воддза теорема серти).

Сідзкӧ ∠1 = ∠2.

Теорема. Кор параллель ногӧн куйлысь кык веськыд визьсӧ вомӧналӧ коймӧд веськыд визь, сэки ӧтарбокса пытшкӧс (ортсы) пельӧсъяслӧн суммаыс лоӧ 180°.

Эскӧдӧм. Мед ∠1 да ∠2 — пытшкӧсса ӧтарбокса пельӧсъяс. Серпас вылысь ми аддзам:

• ∠1 да ∠3 орчча пельӧсъяс, та вӧсна ∠1 + ∠3 = 180°;
• ∠3 = ∠2, найӧ пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс да сійӧн ӧткодьӧсь (теорема серти).

Сідзкӧ ∠1 + ∠2 = 180°.

Ортсыса ӧтарбокса пельӧсъяс йылысь теоремасӧ подулалам сэтшӧм жӧ ногӧн.

Теорема. Кор параллель ногӧн куйлысь кык веськыд визьсӧ вомӧналӧ коймӧд веськыд визь, сэки весьтаса пельӧсъяс ӧтыдждаӧсь.

Эскӧдӧм. Мед ∠1 да ∠2 — весьтаса пельӧсъяс. Серпас вылысь ми аддзам:

• ∠2 = ∠3, найӧ вертикаль пельӧсъяс да сійӧн ӧтыдждаӧсь;
• ∠1 = ∠3, найӧ пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс да сійӧн ӧткодьӧсь (теорема серти).

Сідзкӧ ∠1 = ∠2.

Куимсэрӧгын пельӧсъяслӧн суммаыс

Теорема. Куимсэрӧгын став пельӧслӧн суммаыс 180° ыджда.

Эскӧдӧм. Мед ABC — куимсэрӧг. Арталам сы пельӧсъяслысь суммасӧ: ∠BAC + ∠ABC + ∠BCA. Та могысь гижтам B чут пыр AC-лы параллель ногӧн DE веськыд визьсӧ. Кыдзи аддзам, ∠DBA, ∠ABC да ∠EBC ӧтув артмӧдӧны павтыртӧм пельӧс, сылӧн ыдждаыс 180°. Сы вӧсна мый ∠DBA = ∠BAC, ∠EBC = ∠BCA (найӧ пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс да), ∠BAC, ∠ABC да ∠BCA ӧтув тшӧтш сетасны 180° ыджда. Мӧд ног шуны, ∠BAC + ∠ABC + ∠BCA = 180°.

Теорема. Куимсэрӧглӧн ортсы пельӧсыс лоӧ сылы абу орчча пытшкӧс пельӧсъяс суммакӧд ӧтыджда.

Эскӧдӧм. Мед ABC — куимсэрӧг, ∠ABD — сылӧн ортсы пельӧс. Миянлы колӧ артмӧдны: ∠ABD = ∠BAC + ∠BCA. Кыдзи аддзам, ∠ABD + ∠ABC = 180°, найӧ орчча пельӧсъяс да. Сійӧн ∠ABD = 180° – ∠ABC. Воддза теорема серти кӧ, ∠BAC + ∠ABC + ∠BCA = 180°. Сійӧн 180° – ∠ABC = ∠BAC + ∠BCA. А сідзкӧ, ∠ABD = ∠BAC + ∠BCA.

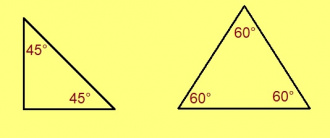
Теорема. Ӧткодь доръяса куимсэрӧгын быд пельӧсыс 60° ыджда.

Эскӧдӧм. Кыдзи ми тӧдам нин, ӧткодь доръяса куимсэрӧгын став пельӧсыс ӧтыдждаӧсь, а суммаын найӧ сетӧны 180°. Сідзкӧ, быд пельӧсыс лоӧ 180° : 3 = 60° ыджда.

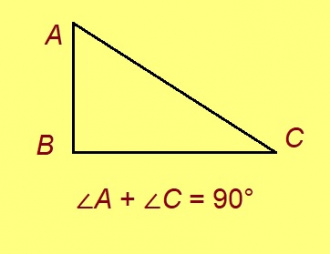
Теорема. Бурпельӧса куимсэрӧгын ёсь пельӧсъясыслӧн суммаыс 90° ыджда.

Эскӧдӧм. Мед ABC куимсэрӧгын ∠B = 90°. Кыдзи ми тӧдам нин, ∠A + ∠B + ∠C = 180°. Сідзкӧ ∠A + ∠C = 180° – ∠B = 90°.

Теорема. Бурпельӧса ӧткодь берда куимсэрӧгын кыкнан ёсь пельӧсыс 45° ыдждаӧсь.

Эскӧдӧм. Кыдзи ми тӧдам нин, бурпельӧса ӧткодь берда куимсэрӧгын ёсь пельӧсъясыс ӧтыдждаӧсь, а суммаын найӧ сетӧны 90°. Сідзкӧ, быд ёсь пельӧсыс лоӧ 90° : 2 = 45° ыджда.

Нёльпельӧсаяс (нёльсэрӧгъяс)

нёльпельӧса, нёльсэрӧг — четырёхугольник
орчча йывъяс (доръяс) — соседние вершины (стороны)
воча йывъяс (доръяс) — противоположные вершины (стороны)

Нёльпельӧсаӧн либӧ нёльсэрӧгӧн шусьӧ нёль чутысь да найӧс сьӧрсьӧн-бӧрсьӧн йитан нёль вундӧгысь тэчӧм мыгӧр. Та дырйи, тайӧ нёль чут письыс сӧмын кыкыс куйлӧны ӧти веськыд визьын, а вундӧгъясыс вермӧны вомӧнасьны сӧмын помъясас.

Нёльпельӧса артмӧдысь чутъяссӧ шуам нёльсэрӧг йывъясӧн, а найӧс йитысь вундӧгъяссӧ — нёльсэрӧг доръясӧн.

Нёльпельӧса кӧ артмӧдӧма A, B, C, D чутъясысь да найӧс йитан AB, BC, CD, DA вундӧгъясысь, сэки гижӧны: ABCD нёльпельӧса.

Нёльсэрӧглысь кык йывсӧ шуам орччаӧн, найӧ кӧ лоӧны ӧти дорлы помъясӧн. Кык дорсӧ шуам орччаӧн, найӧ кӧ петӧны ӧти йылысь.

Нёльсэрӧглысь кык йывсӧ шуам вочаӧн, найӧ кӧ абу орччаӧсь. Кык дорсӧ шуам вочаӧн, найӧ кӧ абу орччаӧсь. Кык воча йыв йитысь вундӧгсӧ шуам диагональӧн.

Нёльпельӧсаын пельӧсъяслӧн суммаыс

Теорема. Нёльсэрӧгын став пельӧслӧн суммаыс 360° ыджда.

Эскӧдӧм. Гижтам нёльсэрӧг пытшкас диагональ (серпас вылын тайӧ AC), коді юкӧ сійӧс кык куимсэрӧг вылӧ. Миян артмӧ: ∠A + ∠B + ∠C + ∠D = ∠BAC + ∠ABC + ∠BCA + ∠CAD + ∠ADC + ∠ADC = 180° + 180° = 360°.

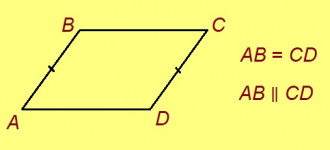
Параллелограмм

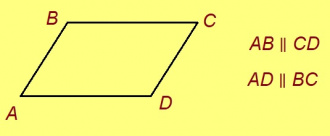
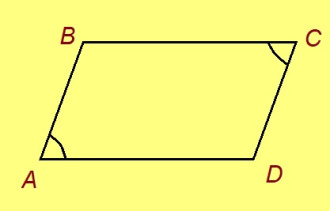
Нёльсэрӧг, кӧні воча доръяс куйлӧны параллель ногӧн, шусьӧ параллелограммӧн.

Параллелограммлӧн тӧдмӧгъяс

1-ӧд тӧдмӧг. Нёльсэрӧгын кӧ воча пельӧсъясыс ӧтыдждаӧсь, тайӧ нёльсэрӧгыс лоӧ параллелограммӧн.

Эскӧдӧм. Мед ABCD — нёльсэрӧг, ∠A = ∠C, ∠B = ∠D. Кыдзи ми тӧдам нин, нёльсэрӧгын став пельӧслӧн суммаыс 360° ыджда. Сідзкӧ, 2∠A + 2∠B = 360°, ∠A + ∠B = 180°. Сыысь петӧ: AD да BC параллель ногаӧсь, ӧд ∠A да ∠B — пытшкӧсса ӧтарбокса пельӧсъяс, а налӧн суммаыс 180°.

Тадзи жӧ артмӧ: AB да CD куйлӧны параллель ногӧн.

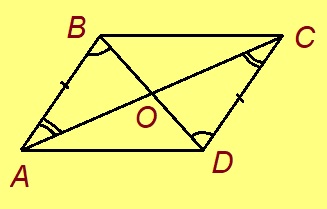
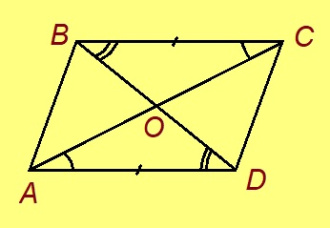
2-ӧд тӧдмӧг. Нёльсэрӧглӧн диагональясыс кӧ вомӧнасьӧны шӧр чутаныс, тайӧ нёльсэрӧгыс лоӧ параллелограммӧн.

Эскӧдӧм. Мед ABCD — нёльсэрӧг, O чут — AC да BD диагональяслӧн вомӧнасянін, AO = OC, BO = OD. AOB да COD пельӧсъяс ӧтыдждаӧсь, найӧ вертикаль пельӧсъяс да. Сідзкӧ ∆AOB = ∆COD медводдза тӧдмӧг серти. Та вӧсна ∠OAB = ∠OCD. Сідзкӧ AB ∥ CD, ӧд ∠OAB да ∠OCD — пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс.

Тадзи жӧ артмӧ: AD ∥ BC.

3-ӧд тӧдмӧг. Нёльсэрӧглӧн кӧ кык воча дор ӧтыдждаӧсь да куйлӧны параллель ногӧн, тайӧ нёльсэрӧгыс лоӧ параллелограммӧн.

Эскӧдӧм. Мед ABCD — нёльсэрӧг, AB = CD, AB ∥ CD. Гижтам AC да BD диагональяс. Мед O — налӧн вомӧнасянін.

∠BAO = ∠DCO да ∠ABO = ∠CDO, ӧд найӧ пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс, а AB да CD — параллельяс.

Миян артмӧ: AB = CD, ∠BAO = ∠DCO, ∠ABO = ∠CDO. Сідзкӧ ∆AOB = ∆COD куимпельӧсаяс ӧткодьлунлӧн мӧд тӧдмӧг серти. Та вӧсна AO = OC, BO = OD. Сідзкӧ ABCD — параллелограмм, воддза теорема серти.

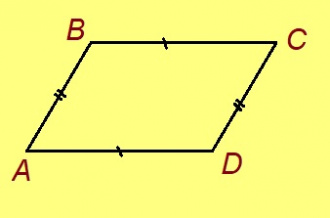
4-ӧд тӧдмӧг. Нёльсэрӧглӧн кӧ кык воча доръяс ӧта-мӧдыскӧд ӧтыдждаӧсь, тайӧ нёльсэрӧгыс лоӧ параллелограммӧн.

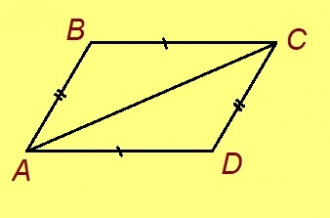
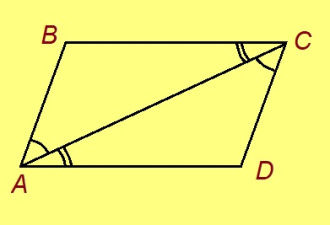
Эскӧдӧм. Мед ABCD — нёльпельӧса, кӧні AB = CD, AD = BC. Гижтам AC диагональ.

Сэки ∆ABC = ∆CDA коймӧд тӧдмӧг серти. Сідзкӧ, ∠BCA = ∠CAD.

Но ∠BCA да ∠CAD — пытшкӧсса ӧтар-мӧдар куйлысь пельӧсъяс. Сідзкӧ BC ∥ AD. Та вӧсна ABCD – параллелограмм, воддза теорема серти.

Параллелограмм торъяланлунъяс

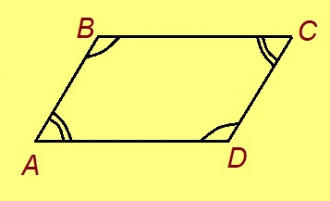
1-ӧд торъяланлун. Параллелограммлӧн воча пельӧсъяс ӧтыдждаӧсь.

Эскӧдӧм. Мед ABCD — параллелограмм. Сэки ∠A + ∠B = 180°, ∠B + ∠C = 180° (найӧ ӧтарбокса пытшкӧс пельӧсъяс да). Сідзкӧ, ∠A = 180° − ∠B = ∠C. Сідзи жӧ артмӧ: ∠B = ∠D.

2-ӧд торъяланлун. Параллелограммлӧн воча доръяс ӧтыдждаӧсь.

Эскӧдӧм. Мед ABCD —параллелограмм. Гижтам сылысь AC диагональсӧ. Сэки ∠BAC = ∠ACD, ∠BCA = ∠CAD, найӧ ӧтар-мӧдар куйлысь пытшкӧс пельӧсъяс да. Сідзкӧ ABC да CDA куимпельӧсаяс ӧткодьӧсь (мӧд тӧдмалан ног серти). Та вӧсна AB = CD, AD = BC.

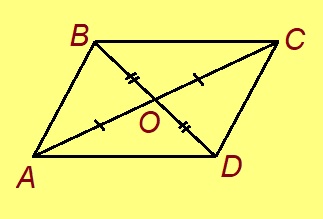
3-ӧд торъяланлун. Параллелограммлӧн диагональяс вомӧнасьӧны асланыс шӧр чутас.

Эскӧдӧм. Мед ABCD — параллелограмм, O — диагональясыслӧн вомӧнасян чут. Сэки ∠OAD = ∠OCB, ∠ODA = ∠OBC, найӧ ӧтар-мӧдар куйлысь пытшкӧс пельӧсъяс да. Ми тӧдам нин: AD = BC. Сідзкӧ AOD да COB куимпельӧсаяс ӧткодьӧсь (мӧд тӧдмалан ног серти). Та вӧсна AO = OC, BO = OD.

Веськыдсэрӧг

Урчитӧм. Параллелограмм, кодлӧн ӧти пельӧсыс веськыд, шусьӧ веськыдсэрӧгӧн.

Пасйӧд. Веськыдсэрӧглӧн став пельӧсыс веськыд.

Теорема. Веськыдсэрӧглӧн диагональясыс ӧтыдждаӧсь.

Эскӧдӧм. Мед ABCD – индӧм веськыдсэрӧг. Сэки BAD да CDA куимсэрӧгъяс ӧткодьӧсь кык катет серти. Сідзкӧ, AC = BD.

Теорема. Параллелограммлӧн диагональясыс кӧ ӧтыдждаӧсь, тайӧ веськыдсэрӧг.

Эскӧдӧм. Мед ABCD – индӧм параллелограмм, AC = BD. Сэки AB = CD, ∠BAD + ∠CDA = 180°. Сідзкӧ, BAD да CDA куимпельӧсаяс ӧткодьӧсь коймӧд тӧдмӧс серти. Та вӧсна ∠BAD = ∠CDA = 90°.

Ромб

Урчитӧм. Параллелограмм шусьӧ ромбӧн, сылӧн кӧ став дорыс ӧтыджда.

Теорема. Ромблӧн диагональ лоӧ сылӧн пельӧсыслӧн биссектриса.

Эскӧдӧм. Мед ABCD – индӧм ромб. Сэки ABC – ӧткодь берда куимпельӧса. Та вӧсна ∠BAC = ∠BCA. Таысь кындзи, ∠BAC = ∠DCA, ∠BCA = ∠DAC кыдзи пытшкӧсса падвежӧнкуйлысьяс. Сідзкӧ, ∠BCA = ∠DCA, ∠BAC = ∠DAC.

Теорема. Ромблӧн диагональяс ӧшанвизьлунаӧсь ӧта-мӧдыслы.

Эскӧдӧм. Мед ABCD – индӧм ромб. Ми тӧдам нин: BD диагональ лоӧ ∠ABC пельӧслӧн биссектриса. AB = BC да, BD ӧшанвизьлуна AC-лы (ӧткодь берда куимпельӧсалӧн торъяланлун серти).

Теорема. Параллелограмм, кодлӧн диагональыс юклӧ пельӧссӧ шӧрипӧв, лоӧ ромб.

Эскӧдӧм. Мед ABCD – индӧм параллелограмм, ∠ABD = ∠CBD. Сідзкӧ, ∠CBD = ∠ADB кыдзи пытшкӧсса падвежӧнкуйлысьяс. Та вӧсна ∠ABD = ∠ADB. Миян артмӧ: ∆DBA ӧткодь берда, AB = AD. Сідзкӧ, ABCD – ромб.

Теорема. Параллелограмм, кодлӧн диагональясыс ӧшанвизьлунаӧсь ӧта-мӧдыслы, лоӧ ромб.

Эскӧдӧм. Мед ABCD – индӧм параллелограмм, сылӧн диагональясыс вомӧнасьӧны O чутын. Сэки AOB да BOC куимпельӧсаяс ӧткодьӧсь кык катет серти. Та вӧсна OA = OB.

Квадрат

Урчитӧм. Нёльпельӧса шусьӧ квадратӧн, сылӧн кӧ став дорыс ӧтыджда да став пельӧсыс 90° ыджда.

Кывкӧртӧд. Квадратлӧн диагональясыс 1) ӧтыдждаӧсь, 2) ӧта-мӧдыслы ӧшанвизьлунаӧсь, 3) шӧрипӧв юклӧны квадратыслысь пельӧсъяссӧ.

Кывкӧртӧд. Квадратлӧн диагональ юклӧ сійӧс ӧткодь берда веськыдпельӧса кык куимсэрӧг вылӧ.

Кывкӧртӧд. Квадратлӧн кык диагональ юклӧны сійӧс ӧткодь берда веськыдпельӧса нёль куимсэрӧг вылӧ.

Трапеция

Урчитӧм. Нёльпельӧса шусьӧ трапецияӧн, сылӧн кӧ воча кык дор ӧтнырвизяӧсь, а мӧд воча кык дор абу ӧтнырвизяӧсь.

Ӧтнырвизя доръясыс шусьӧны трапеция подувъясӧн. Мӧд кык дор шусьӧны трапециялӧн боквыв доръясӧн.

Веськыдпельӧса трапециялӧн ӧти пельӧсыс веськыд.

Ӧткодь берда трапециялӧн боквыв доръясыс ӧтыдждаӧсь.

Теорема. Ӧткодь берда трапециялӧн подувбердса пельӧсъяс ӧтыдждаӧсь.

Эскӧдӧм. Мед ABCD – индӧм трапеция, BC да AD – сылӧн подувъяс, AB = CD. Мед BE ∥ CD, E чут куйлӧ AD вундӧг вылын. Сідзкӧ, BCDE – параллелограмм да BE = CD, ∠CDA = ∠BEA. Та вӧсна AB = BE да ∠BAE = ∠BEA. Миян артмис: ∠CDA = ∠BAD.

Теорема. Трапециялӧн кӧ подувбердса ӧтыдждаӧсь, сійӧ ӧткодь берда.

Эскӧдӧм. Мед ABCD – индӧм трапеция, BC да AD – сылӧн подувъяс, ∠CDA = ∠BAD. Мед BE ∥ CD, E чут куйлӧ AD вундӧг вылын. Сідзкӧ, BCDE – параллелограмм да BE = CD, ∠CDA = ∠BEA. Та вӧсна ∠BAE = ∠BEA. Сідзкӧ, AB = BE = CD.