Планиметрия курс − 2
Медводдза юкӧн тані.
Содержание
Фалеслӧн теорема
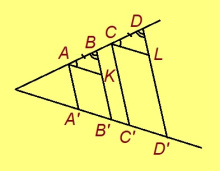
Фалеслӧн теорема. Мед кутшӧмкӧ пельӧслӧн ӧти дорас эмӧсь A, B, C да D чутъяс, а мӧд дорас — A’, B’, C’ да D’ чутъяс, та дырйи AA’, BB’, CC’, DD’ куйлӧны параллель ногӧн, а AB да CD вундӧгъяс ӧткузьтаӧсь. Сэки A’B’ = C’D’.
Подулалӧм. Гижтам A’C’-лы параллель ногӧн веськыд визьяс A да C чутъяс пыр. Ӧтиыс вомӧнасьӧ BB’-кӧд K чутын, мӧдыс вомӧнасьӧ DD’-кӧд L чутын. Миян артмӧ: AA’B’K да CC’D’L — параллелограммъяс.
Параллелограммлӧн аслун серти, A’B’ = AK, C’D’ = CL.
Петкӧдлам, мый AK = CL. Сы могысь видлалам ABK да CDL куимсэрӧгъяссӧ.
Миян артмӧ:
1) AK ∥ CL (найӧ кыкнанныс A’C’-лы параллельяс да), ∠KAB да ∠LCD — весьтаса пельӧсъяс; сідзкӧ ∠KAB = ∠LCD;
2) BK ∥ LD (видзӧдӧй теоремалысь формулировка), ∠KBA да ∠LDC — весьтаса пельӧсъяс; сідзкӧ ∠KBA = ∠LDC;
3) AB = CD (видзӧдӧй теоремалысь формулировка).
Сідзкӧ ABK да CDL куимсэрӧгъяс ӧткодьӧсь мӧд тӧдмӧг серти. Та вӧсна AK = CL.
Миян артмис: A’B’ = AK, C’D’ = CL, AK = CL. Сідзкӧ A’B’ = C’D’.
Шӧр визь
Куимсэрӧгын шӧр визь
Куимсэрӧгса шӧр визьӧн шуам кык дорсьыс шӧр чутъяссӧ йитан вундӧг.
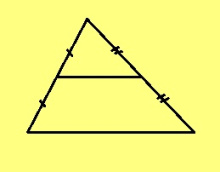
Теорема. Куимсэрӧгын шӧр визь лоӧ коймӧд дорлы параллельӧн.
Подулалӧм. Мед ABC — куимсэрӧг, D — AB-лӧн шӧр чут, E — BC-лӧн шӧр чут. Гижтам D чут пыр AC-лы параллель. Сійӧ вомӧнасьӧ BC-кӧд F чутын. AD = DB, DF ∥ AC; сідзкӧ, Фалеслӧн теорема серти, CF = FB. Та вӧсна F — BC-лӧн шӧр чут, кыдзи и E чут. Сідзкӧ F = E да DE ∥ AC.
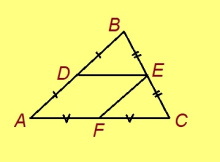
Теорема. Куимсэрӧгын шӧр визьыс лоӧ сыкӧд параллель ногӧн куйлысь дорлӧн джын кузьта.
Подулалӧм. Мед ABC — куимсэрӧг, D — AB-лӧн шӧр чут, E — BC-лӧн шӧр чут, F — AC-лӧн шӧр чут. Кыдзи ми тӧдам нин, DE ∥ AC, EF ∥ AB, найӧ ABC-лӧн шӧр визьяс да. Сідзкӧ ADEF — параллелограмм. Параллелограммлӧн аслун серти, DE = AF. Но F — AC-лӧн шӧр чут; сідзкӧ AF = AC/2. Со миян и артмис: DE = AC/2.
Трапецияын шӧр визь
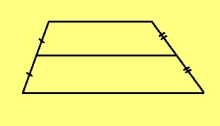
Трапецияса шӧр визьӧн шуам кыкнан боквыв дорсьыс шӧр чутъяссӧ йитан вундӧг.
Теорема. Трапецияын шӧр визьыс лоӧ подувъяслы параллельӧн.
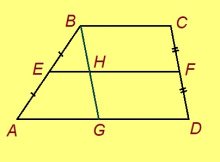
Подулалӧм. Мед ABCD — трапеция, AB да CD — сылӧн боквыв доръяс, E — AB-лӧн шӧрчут, F — CD-лӧн шӧрчут. Гижтам E чут пыр AD-лы параллель. Сійӧ вомӧнасьӧ CD-кӧд G чутын. AE = BE, EG ∥ AD ∥ BC; сідзкӧ, Фалес теорема серти, CG = GD. Та вӧсна G — CD-лӧн шӧрчут, кыдзи и F чут. Сідзкӧ F = G да EF ∥ AD.
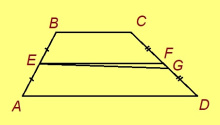
Теорема. Трапецияын шӧр визьыс лоӧ сы подувъяс суммалӧн джын кузьта.
Подулалӧм. Мед ABCD — трапеция, AD да BC — сылӧн подувъяс, EF — шӧр визьыс. Гижтам B чут пыр CD‐лы параллель. Сылысь AD‐кӧд вомӧнасянінсӧ пасъям G‐ӧн; EF да BG‐лысь вомӧнасян чутсӧ пасъям H‐ӧн. Кыдзи ми тӧдам нин, EF лоӧ подувъяслы параллельӧн. Сідзкӧ HBCF да GHFD — параллелограммъяс. А параллелограммын воча доръясыс век ӧткузяӧсь. Сідзкӧ BC = HF = GD.
Таысь кындзи, AG ∥ EH, AE = BE. Фалеслӧн теорема серти, BH = HG. Сідзкӧ EH лоӧ ABG куимсэрӧгын шӧр визьнас. Войдӧр ми тӧдмалім нин: куимсэрӧгын шӧр визьыс лоӧ сылы параллель дорлӧн джын кузьта. Сідзкӧ EH = AG/2.
Миян артмӧ:
EF = EH + HF = BC + AG/2 = BC + (AD − GD)/2 =
= BC + (AD − BC)/2 = (AD + BC)/2.
Фалеслӧн мӧд теорема
Урчитӧм. AB да CD, EF да GH вундӧгъяс пропорцияынӧсь, AB : CD да EF : GH юкасъяс кӧ ӧткодьӧсь: AB : CD = EF : GH.
Мед AB да CD, EF да GH вундӧгъяс кӧ пропорцияынӧсь. Сэки 1) AB да EF, CD да GH пропорцияынӧсь; 2) AB∙GH = CD∙EF.
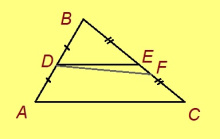
Теорема. Мед E да F чутъяс куйлӧны AB да CD вундӧгъяс пытшкын, AE да BE, CF да DF вундӧгъяс пропорцияынӧсь. Сэки AE да AB, CF да CD вундӧгъяс пропорцияынӧсь. Эскӧдӧм. AE : BE = CF : DF; сідзкӧ, BE : AE = DF : CF. Та вӧсна (BE : AE) + 1 = (DF : CF) + 1, кытысь артмӧдам (BE + AE) : AE = (DF + CF) : CF. Аксиома серти, BE + AE = AB, DF + CF = CD. Сідзкӧ, AB : AE = CD : CF, кытысь AE : AB = CF : CD.
Фалес теорема. Мед A да B чутъяс куйлӧны O йыла пельӧслӧн ӧти дор вылын, C да D чутъяс – мӧд дор вылын, AC ∥ BD. Сэки OA да OB, OC да OD вундӧгъяс пропорцияынӧсь.
Эскӧдӧм. Мед, шуам, A чут куйлӧ O да B чутъяс костын. Петкӧдлам: OA : AB = OC : CD. Медбӧръя теорема серти, миян артмас OA : OB = OC : OD. Ми кутам подулавны теоремасӧ сӧмын сэк, кор OA : AB = p : q, кӧні p да q – дзонь плюса лыдъяс. Юклам OA вундӧгсӧ p пельӧ (артмӧм вундӧгъясыс OA : p кузьтаӧсь); AB вундӧгсӧ юклам q пельӧ (артмӧм вундӧгъясыс AB : q кузьтаӧсь). Пропорцияысь аддзам: OA : p = AB : q. Сідзкӧ, OB вундӧг юклӧма p + q пельӧ, став артмӧм вундӧгыс ӧтыджда. Нуӧдам артмӧм вундӧгъяслӧн помъяс пыр BD-кӧд ӧтнырвизя веськыдъяс. Фалеслӧн медводдза теорема серти, найӧ юклӧны OD вундӧгсӧ ӧтыджда вундӧгъяс артмӧдӧмӧн; OC вундӧгыс кутӧ p ӧтыджда вундӧг, CD вундӧгыс – q ӧтыджда вундӧг. Сідзкӧ, OC : CD = p : q = OA : AB.
Теорема. Мед A да B чутъяс куйлӧны O йыла пельӧслӧн ӧти дор вылын, C да D чутъяс – мӧд дор вылын, OA да OB, OC да OD вундӧгъяс пропорцияынӧсь. Сэки AC ∥ BD.
Эскӧдӧм. Нуӧдам A чут пыр BD-кӧд ӧтнырвизя веськыдӧс. Мед сійӧ вомӧнасьӧ пельӧслӧн мӧд доркӧд E чутын. Фалес теорема серти, OA : OB = OE : OD. Сідзкӧ, OE = OA∙OD/OB = OC. Та вӧсна E = C да AC ∥ BD.
Ӧтсяма куимпельӧсаяс
Урчитӧм. ABC да A’B’C’ куимпельӧсаяс ӧтсямаӧсь (∆ABC ~ ∆A’B’C’), налӧн пельӧсъясыс кӧ гозйӧн-гозйӧн ӧтыдждаӧсь (∠A = ∠A’, ∠B = ∠B’, ∠C = ∠C’) да доръясыс пропорцияынӧсь (AB : A’B’ = BC : B’C’ = CA : C’A’).
Теорема. Мед ABC – куимпельӧса, D чут куйлӧ AB дор вылын, E чут куйлӧ AC дор вылын, DE ∥ BC. Сэки ABC да ADE куимпельӧсаяс ӧтсямаӧсь.
Эскӧдӧм. ∠D = ∠B, ∠E = ∠C кыдзи весьтаса пельӧсъяс; ∠A куимпельӧсаясыслӧн ӧтувъя пельӧс. Фалес теорема серти, AD : AB = AE : AC. Колис петкӧдлыны: AD : AB = DE : BC. Мед F чут куйлӧ AB дор вылын, BF = AD; G чут куйлӧ BC дор вылын, FG ∥ AC. Сэки ∠EAD = ∠GFB, ∠EDA = ∠GBF кыдзи весьтаса пельӧсъяс. Сідзкӧ, EAD да GFB куимпельӧсаяс ӧткодьӧсь мӧд тӧдмӧс серти. Та вӧсна ED = GB. Фалес теорема серти, GB : BC = BF : AB. Сідзкӧ, ED : BC = AD : AB.
Куимпельӧсаяс ӧтсямалун медводдза тӧдмӧс. Мед ABC да A’B’C’ куимпельӧсаяслӧн ∠A = ∠A’, ∠B = ∠B’. Сэки ABC да A’B’C’ куимпельӧсаяс ӧтсямаӧсь.
Эскӧдӧм. Мед, шуам, A’B’ ≤ AB. Мед M чут куйлӧ AB дор вылын, AM = A’ B’, N чут куйлӧ AC дор вылын, AN = A’C’. Сэки ∆AMN = ∆A’B’C’ медводдза тӧдмӧс серти. Та вӧсна ∠NMA = ∠C’B’A’ = ∠CBA. Сідзкӧ, MN ∥ BC. Воддза теорема серти, AMN да ABC куимпельӧсаяс ӧтсямаӧсь. Сідзкӧ, A’B’C’ да ABC куимпельӧсаяс ӧтсямаӧсь.
Куимпельӧсаяс ӧтсямалун мӧд тӧдмӧс. Мед ABC да A’B’C’ куимпельӧсаяслӧн ∠A = ∠A’, AB : A’B’ = AC : A’C’. Сэки ABC да A’B’C’ куимпельӧсаяс ӧтсямаӧсь.
Эскӧдӧм. Мед, шуам, A’B’ ≤ AB. Мед M чут куйлӧ AB дор вылын, AM = A’ B’, N чут куйлӧ AC дор вылын, AN = A’C’. Сэки ∆AMN = ∆A’B’C’ медводдза тӧдмӧс серти да, AB : AM = AC : AN. Фалес мӧдара теорема серти, MN ∥ BC. Миян артмӧ: ∆AMN ~ ∆ABC. Та вӧсна A’B’C’ да ABC куимпельӧсаяс ӧтсямаӧсь.
Куимпельӧсаяс ӧтсямалун коймӧд тӧдмӧс. Мед ABC да A’B’C’ куимпельӧсаяслӧн AB : A’B’ = AC : A’C’ = BC : B’C’. Сэки ABC да A’B’C’ куимпельӧсаяс ӧтсямаӧсь.
Эскӧдӧм. Мед k = AB : A’B’ = AC : A’C’. Мед M чут куйлӧ AB дор вылын, AM = A’ B’, N чут куйлӧ AC дор вылын, AN = A’C’. Сэки AMN да ABC куимпельӧсаяс ӧтсямаӧсь да AM : AB = AN : AC = MN : BC. Но AM : AB = A’B’ : AB = k. Сідзкӧ, MN = k∙BC = B’C’. Та вӧсна AMN да A’B’C’ куимпельӧсаяс ӧткодьӧсь коймӧд тӧдмӧс серти. Сідзкӧ, ABC да A’B’C’ куимпельӧсаяс ӧтсямаӧсь.
Кывкӧртӧд. Ӧткодь доръяса куимпельӧсаяс ӧта-мӧдыскӧд ӧтсямаӧсь.
Кывкӧртӧд. Ӧткодь берда веськыдпельӧса куимсэрӧгъяс ӧта-мӧдыскӧд ӧтсямаӧсь.
Кывкӧртӧд. Ӧткодь берда куимпельӧсаяслӧн кӧ йывса пельӧсъяс ӧтыдждаӧсь, тайӧ куимпельӧсаясыс ӧтсямаӧсь.
Кывкӧртӧд. Ӧткодь берда куимпельӧсаяслӧн кӧ подувбердса пельӧсъяс ӧтыдждаӧсь, тайӧ куимпельӧсаясыс ӧтсямаӧсь.
Кывкӧртӧд. Веськыдпельӧса куимсэрӧгъяслӧн кӧ эмӧсь ӧтыджда гипотенузабердса пельӧсъяс, тайӧ куимсэрӧгъясыс ӧтсямаӧсь.
Кывкӧртӧд. Веськыдпельӧса куимсэрӧгъяслӧн кӧ катетъяс пропорцияынӧсь, тайӧ куимсэрӧгъясыс ӧтсямаӧсь.
Теорема. Мед ABC да A’B’C’ – ӧтсяма куимпельӧсаяс, BL да B’L’ – налӧн биссектрисаяс. Сэки BL : B’L’ = AB : A’B’.
Эскӧдӧм. BL да B’L’ биссектрисаяс, та вӧсна ∠ABL = ∠ABC/2 = ∠A’B’C’/2 = ∠A’B’L’. ∆ABC ~ ∆A’B’C’; сідзкӧ, ∠BAL = ∠B’A’L’. Та понда ∆ABL ~ ∆A’B’L’ медводдза тӧдмӧс серти. Сідзкӧ, BL : B’L’ = AB : A’B’.
Теорема. Мед ABC да A’B’C’ – ӧтсяма куимпельӧсаяс, BM да B’M’ – налӧн медианаяс. Сэки BM : B’M’ = AB : A’B’.
Эскӧдӧм. BM да B’M’ медианаяс, та вӧсна AM = AC/2, A’M’ = A’C’/2, кытысь артмӧдам: AM : A’M’ = AB : A’B’. ∆ABC ~ ∆A’B’C’; сідзкӧ, ∠BAM = ∠B’A’M’. Та понда ∆ABM ~ ∆A’B’M’ мӧд тӧдмӧс серти. Сідзкӧ, BM : B’M’ = AB : A’B’.
Теорема. Мед ABC да A’B’C’ – ӧтсяма куимпельӧсаяс, BH да B’H’ – налӧн судтаяс. Сэки BH : B’H’ = AB : A’B’.
Эскӧдӧм. BH да B’H’ судтаяс, та вӧсна ∠AHB = 90º = ∠A’H’B’. ∆ABC ~ ∆A’B’C’; сідзкӧ, ∠BAH = ∠B’A’H’. Та понда ∆ABH ~ ∆A’B’H’ медводдза тӧдмӧс серти. Сідзкӧ, BH : B’H’ = AB : A’B’.
Теорема. Мед ABC куимпельӧсаын AK да BM – медианаяс, O – налӧн вомӧнасян чут. Сэки AO : OK = BO : OM = 2 : 1.
Эскӧдӧм. KM – ABC куимпельӧсалӧн шӧр визь. Сідзкӧ, KM ∥ AB, AB : KM = 2 : 1. Та вӧсна ∠KAB = ∠AKM, ∠MBA = ∠BMK (пельӧсъясыс ӧтыдждаӧсь кыдз пытшкӧсса падвежӧнкуйлысьяс). Сідзкӧ, ∆OAB ~ ∆OKM медводдза тӧдмӧс серти. Миян артмӧ: AO : OK = BO : OM = AB : KM = 2 : 1.
Кывкӧртӧд. Куимпельӧсалӧн медианаяс вомӧнасьӧны ӧти чутын.
Эскӧдӧм. Мед AK, BM да CN – ABC куимпельӧсалӧн медианаяс, O – AK да BM-лӧн вомӧнасян чут, O’ – AK да CN-лӧн вомӧнасян чут. Сэки AO : OK = 2 : 1, AO’ : O’K = 2 : 1. Та вӧсна O’ = O.
Теорема. Мед BL – ABC куимпельӧсалӧн биссектриса. Сэки AL : LC = AB : BC.
Эскӧдӧм. BL кӧ нӧшта лоӧ судтаӧн, ∆ABL = ∆CBL мӧд тӧдмӧс серти; сідзкӧ, AL : LC = AB : BC = 1. Мед, шуам, ALB пельӧс ёсь. Мед M чут куйлӧ BL визьньӧв вылын, AM = BM. Сэки ∠AML = ∠ALM (ӧткодь берда куимпельӧсаын подувбердса пельӧсъяс), ∠ALM = ∠BLC (сувтса пельӧсъяс). Сідзкӧ, ∠ABM = ∠CBL, ∠AMB = ∠CLB. Та вӧсна ∆ABM ~ ∆CBL медводдза тӧдмӧс серти да AB : BC = AM : LC = AL : LC.
Теорема. Мед ABC – веськыдпельӧса куимсэрӧг, B – сылӧн веськыд пельӧс, BH – судтаыс. Сэки ABC, AHB да BHC куимпельӧсаяс ӧтсямаӧсь.
Эскӧдӧм. ABC, AHB да BHC – веськыдпельӧса куимсэрӧгъяс, кодъяслӧн ∠BAC = ∠HAB = ∠HBC. Сідзкӧ ∆ABC ~ ∆AHB ~ ∆BHC медводдза тӧдмӧс серти.
Теорема. Мед ABC – веськыдпельӧса куимсэрӧг, B – сылӧн веськыд пельӧс, BH – судтаыс. Сэки BH2 = AH∙HC.
Эскӧдӧм. Воддза теорема серти, ∆AHB ~ ∆BHC; сідзкӧ, AH : HB = HB : HC. Пропорция медшӧр торъяланлун серти, BH2 = AH∙HC.
Пифагор теорема. Веськыдпельӧса куимсэрӧглӧн гипотенуза квадрат ӧтыджда кык катет квадрат содтаскӧд.
Эскӧдӧм. Мед ABC – веськыдпельӧса куимсэрӧг, B – сылӧн веськыд пельӧс. ∆ABC ~ ∆AHB да, AH : AB = AB : AC; ∆ABC ~ ∆BHC да, HC : BC = BC : AC. Сідзкӧ, AC∙AH = AB2, AC∙HC = BC2. Содтам тайӧ кык ӧткодьлун: AC∙(AH + AC) = AB2 + BC2. Миян артмӧ: AC2 = AB2 + BC2.
Кывкӧртӧд. Мед ABC да A’B’C’ – веськыдпельӧса куимсэрӧгъяс, B да B’ – веськыд пельӧсъяс, AB : A’B’ = AC : A’C’. Сэки ABC да A’B’C’ куимпельӧсаяс ӧтсямаӧсь.
Эскӧдӧм. Мед AB = k∙A’B’. Сэки AC = k∙A’C’. Пифагор теорема серти, BC2 = AC2 – AB2 = k2(A’C’2 – A’B’2) = k2B’C’2, кытысь артмӧ BC = k∙B’C’. Та вӧсна AB : A’B’ = BC : B’C’ да куимпельӧсаясыс ӧтсямаӧсь кык катет серти.
Теорема. Куимпельӧсалӧн кӧ ӧти дор квадрат ӧтыджда мӧд кык дор квадрат содтаскӧд, тайӧ веськыдпельӧса куимсэрӧг.
Эскӧдӧм. Мед ABC куимпельӧсалӧн AB2 + BC2 = AC2. Босьтам веськыдпельӧса куимсэрӧг AB да BC кузьта катетъясӧн. Пифагор теорема серти, сылӧн гипотенуза AC кузьта. Сідзкӧ, тайӧ куимсэрӧгыс ӧткодь ABC-кӧд коймӧд тӧдмӧс серти. Та вӧсна ABC пельӧсыс веськыд.
Видлӧг. Египетса куимсэрӧг – тайӧ куимпельӧса, кодлӧн доръясыс лӧсялӧны 3 : 4 : 5 моз. 52 = 32 + 42 да, тайӧ веськыдпельӧса куимсэрӧг.
Чутсянь веськыд визьӧдз ылнаӧн шусьӧ чутсяньыс веськыд визьӧдз нуӧдӧм ӧшанвизь кузьта.
Теорема. Пельӧс биссектрисавывса быд чут ӧтылнаын пельӧс доръяссянь.
Эскӧдӧм. Мед A – пельӧслӧн йыв, M чут куйлӧ биссектриса вылын, K да L чутъяс куйлӧны пельӧс доръяс вылын, MK ⊥ AK, ML ⊥ AL. Сідзкӧ, ∆MKA = ∆MLA гипотенуза да ёсь пельӧс серти. Та вӧсна MK = ML.
Теорема. Пельӧс пытшкӧсса чут кӧ пельӧс доръяссяньыс ӧтылнаын, сійӧ куйлӧ биссектриса вылын.
Эскӧдӧм. Мед A – пельӧслӧн йыв, M чут куйлӧ пельӧс пытшкын, K да L чутъяс куйлӧны пельӧс доръяс вылын, MK ⊥ AK, ML ⊥ AL, MK = ML. Сідзкӧ, ∆MKA = ∆MLA гипотенуза да катет серти. Та вӧсна ∠MAK = ∠MAL.
Теорема. Куимпельӧсалӧн биссектрисаяс вомӧнасьӧны ӧти чутын.
Эскӧдӧм. Мед ABC куимпельӧсаса A да B пельӧсъяслӧн биссектрисаяс вомӧнасьӧны O чутын. Сэки O чут ӧтылнаын AB да AC доръяссянь; сійӧ жӧ ӧтылнаын AB да BC доръяссянь. Та вӧсна сійӧ ӧтылнаын AC да BC доръяссянь. Сідзкӧ, сійӧ куйлӧ C пельӧс биссектриса вылын. Миян артмис: куимнан биссектриса мунӧны O чут пыр.
Теорема. Вундӧг шӧр ӧшанвизьвывса быд чут вундӧг помъяссянь ӧтылнаынӧсь.
Эскӧдӧм. Мед AB – индӧм вундӧг, C – сылӧн шӧрчут, l – шӧр ӧшанвизь, M чут куйлӧ l вылын. Сэки MCA да MCB куимпельӧсаяс ӧткодьӧсь кык катет серти. Сідзкӧ, AM = BM.
Теорема. Чут кӧ вундӧг помъяссянь ӧтылнаын, сійӧ куйлӧ шӧр ӧшанвизь вылын.
Эскӧдӧм. Мед AB – индӧм вундӧг, MA = MB. Сэки AMB – ӧткодь берда куимпельӧса. Мед MC – сылӧн биссектриса. Сэки MC – медиана да судта, та вӧсна сійӧ AB вундӧглӧн шӧр ӧшанвизь.
Теорема. Куимпельӧса доръяслӧн шӧр ӧшанвизьяс вомӧнасьӧны ӧти чутын.
Эскӧдӧм. Мед ABC – индӧм куимпельӧса, O – AB да AC доръяслӧн шӧр ӧшанвизьяс вомӧнасян чут. Сэки OA = OB, OA = OC. Сідзкӧ, OB = OC. Та вӧсна O чут куйлӧ BC дорлӧн шӧр ӧшанвизь вылын.
Теорема. Куимпельӧсалӧн судтаяс вомӧнасьӧны ӧти чутын.
Эскӧдӧм. Мед ABC – сетӧм куимпельӧса, AK, BL, CM – сылӧн судтаяс. Нуӧдам A, B да C чутъяс пыр BC-кӧд, AC-кӧд да AB-кӧд ӧтнырвизя веськыдъяс. Мед найӧ вомӧнасьӧны A’, B’ да C’ чутъясын. ABA’C да AC’BC – параллелограммъяс. Сідзкӧ, C’B = AC = BA’ да BL – A’C’ дорлӧн шӧр ӧшанвизь. Сідзи жӧ миян артмӧ: AK – B’C’ дорлӧн шӧр ӧшанвизь, CM – A’B’ дорлӧн шӧр ӧшанвизь. Та вӧсна найӧ вомӧнасьӧны ӧти чутын.
Менелай теорема. Мед B чут куйлӧ AC вундӧгын, F чут куйлӧ AE вундӧгын, BE да CF вомӧнасьӧны D чутын. Сэки (AB : BC)∙(CD : DF)∙(EF : AE) = 1.
Эскӧдӧм. Мед FG ӧтнырвизя AB-кӧд. Сэки ABE да FGE куимпельӧсаяс ӧтсямаӧсь, та вӧсна FE : AE = GF : AB; FGD да CBD куимпельӧсаяс ӧтсямаӧсь, та вӧсна FG : DF = BC : CD. Сідзкӧ, (FE : AE)∙AB = (BC : CD)∙DF, кытысь (AB : BC)∙(CD : DF)∙(EF : AE) = 1.
Чева теорема. Мед ABC куимпельӧсаын K, L да M чутъяс куйлӧны BC, AC да AB вылын. Мед AK, BL да CM вундӧгъяс вомӧнасьӧны ӧти чутын. Сэки (AM : MB)∙(BK : KC)∙(CL : AL) = 1.
Эскӧдӧм. Мед O – AK, BL да CM вундӧгъяслӧн вомӧнасян чут. Менелай теорема серти, (AM : MB)∙(BO : OL)∙(CL : AC) = 1, (CK : KB)∙(BO : OL)∙(AL : LC) = 1. Сідзкӧ, (AM : MB)∙(BK : KC)∙(CL : AL) = 1.
Теорема (мӧдара). Мед ABC куимпельӧсаын K, L да M чутъяс куйлӧны BC, AC да AB вылын. Мед (AM : MB)∙(BK : KC)∙(CL : AL) = 1. Сэки AK, BL да CM вундӧгъяс вомӧнасьӧны ӧти чутын.
Эскӧдӧм. Мед M’ чут куйлӧ AB вылын, AK, BL да CM’ вомӧнасьӧны ӧти чутын. Чева теорема серти, (AM’ : MB’)∙(BK : KC)∙(CL : AL) = 1. Сідзкӧ, AM : MB = AM’ : MB’. Та вӧсна M = M’.
Кывкӧртӧд. Куимпельӧсалӧн медианаяс вомӧнасьӧны ӧти чутын.
Кывкӧртӧд. Куимпельӧсалӧн биссектрисаяс вомӧнасьӧны ӧти чутын.
Эскӧдӧм. Мед AK, BL да CM – ABC куимпельӧсалӧн биссектрисаяс. Сэки AM : MB = AC : CB, BK : KC = BA : AC, CL : LA = CB : BA. Сідзкӧ, (AM : MB)∙(BK : KC)∙(CL : AL) = (AC : CB)∙(BA : AC)∙(CB : BA) = 1. Воддза теорема серти, AK, BL да CM вомӧнасьӧны ӧти чутын.
Кывкӧртӧд. Куимпельӧсалӧн судтаяс вомӧнасьӧны ӧти чутын.
Эскӧдӧм. Мед AK, BL да CM – ABC куимпельӧсалӧн судтаяс. ALB да AMC куимпельӧсаяс ӧтсямаӧсь медводдза тӧдмӧс серти; сідзкӧ, AM : LA = CM : BL. Сэтшӧм жӧ ногӧн артмӧдам: BK : MB = AK : CM, CL : CK = BL : AK. Сідзкӧ, (AM : MB)∙(BK : KC)∙(CL : AL) = (AM : AL)∙(BK : MB)∙(CL : KC) = (CM : BL)∙(AK : CM)∙(BL : AK) = 1. Та вӧсна AK, BL да CM вомӧнасьӧны ӧти чутын.
Эрд
Урчитӧм. Мыгӧр шусьӧ прӧстӧйӧн, сійӧс кӧ позьӧ юклыны некымын куимпельӧса вылӧ.
Аксиома. Быд прӧстӧй мыгӧрлӧн эм эрд – минустӧм лыд. Эрдлӧн торъяланлунъяс со кутшӧмӧсь: 1) прӧстӧй мыгӧр кӧ юклӧма некымын прӧстӧй мыгӧр вылӧ, сылӧн эрдыс ӧтыджда юкӧнъясыслӧн эрдъяс суммаыскӧд;
S = S1 + S2 + S3 + S4 + S5
2) ӧткодь куимпельӧсаяслӧн эрдъясыс ӧтыдждаӧсь;
3) квадратлӧн дор кузьта кӧ лоӧ 1, сылӧн эрдыс лоӧ 1.
Кык веськыдсэрӧг ӧткодьӧсь, налӧн кӧ лӧсялана доръясыс ӧтыдждаӧсь.
Висьталӧм. Ӧткодь кык веськыдсэрӧглӧн эрдъясыс ӧтыдждаӧсь.
Эскӧдӧм. Мед ABCD да A’B’C’D’ веськыдсэрӧгъяс ӧткодьӧсь: AB = A’B’, BC = B’C’. Нуӧдам BD да B’D’ диагональяссӧ. Миян артмӧ: ABD, CBD, A’B’D’, C’B’D’ куимпельӧсаяс ӧткодьӧсь кык катет серти. Сідзкӧ, налӧн ӧткодь эрдъясыс да SABCD = SABD + SCBD = SA’B’D’ + SC’B’D’ = SA’B’C’D’.
Висьталӧм. Мед ABCD да A’B’C’D’ – веськыдсэрӧгъяс, AB = A’B’, BC дорыс n пӧв ыджыдджык B’C’ дорысь (n – эма лыд: 1, 2, 3, 4....). Сэки ABCD-лӧн эрдыс n пӧд ыджыдджык A’B’C’D’-лӧн эрдысь.
Эскӧдӧм. Юклам BC дорсӧ n ӧтыджда вундӧг вылӧ да нуӧдам юкан чутъяс пыр веськыд визьяс AB-кӧд параллель ногӧн. Сідз ABCD лоас юклӧма A’B’C’D’-кӧд ӧткодь n веськыдсэрӧг вылӧ. Та вӧсна SABCD = n∙SA’B’C’D’.
Висьталӧм. Мед ABCD да A’B’C’D’ – веськыдсэрӧгъяс, AB = A’B’, BC : B’C’ = m : n (m да n – эма лыдъяс). Сэки ABCD-лӧн эрдыс m/n пӧв ыджыдджык A’B’C’D’-лӧн эрдысь.
Эскӧдӧм. Мед KLMN – веськыдсэрӧг, KL = AB, LM = n∙BC. Миян артмӧ: SABCD : SKLMN = 1 : n, SA’B’C’D’ : SKLMN = 1 : m. Сідзкӧ, SABCD : SA’B’C’D’ = m : n.
Кывкӧртӧд. Мед ABCD да A’B’C’D’ – веськыдсэрӧгъяс, AB = A’B’. Сэки ABCD да A’B’C’D’-лӧн эрдъясыс лӧсялӧны BC : B’C’ моз.
Кывкӧртӧд. Мед веськыдсэрӧглӧн доръясыс a да b кузьтаяс. Сэки сылӧн эрдыс лоӧ ab.
Кывкӧртӧд. Веськыдпельӧса куимсэрӧглӧн эрдыс лоӧ катетъясыс кузьтаяслӧн лыдмӧдас джын.
Эскӧдӧм. Мед ABC – индӧм куимсэрӧг, AB = a да BC = c – сылӧн катетъяс. Артмӧдам ABCD веськыдсэрӧгсӧ. Сідзкӧ, ∆ABC = ∆ADC, ac = SABCD = 2S∆ABC. Та вӧсна S∆ABC = ac/2.
Теорема. Параллелограммлӧн эрдыс лоӧ ӧти дорыс да сы вылӧ нуӧдӧм судтаыс лыдмӧдас.
Эскӧдӧм. Мед ABCD – индӧм параллелограмм, ∠A – сылӧн тшӧтшыд пельӧс. Нуӧдам BK да DL судтаяссӧ. Миян артмӧ KBLD веськыдсэрӧг; сійӧ юклӧма ABCD параллелограмм да KBA, LDC веськыдпельӧса куимсэрӧгъяс вылӧ. Мед AD = a, AK = b, BK = h. Сідзкӧ, SABCD = SKBLD – SKBA – SLDC = (a + b)h – bh/2 – bh/2 = ah.
Теорема. Куимпельӧсалӧн эрдыс лоӧ ӧти дорыс да сы вылӧ нуӧдӧм судтаыс лыдмӧдас джын.
Эскӧдӧм. Мед ABC – индӧм куимпельӧса, BH – сылӧн судта, AC = a, BH = h. Артмӧдам ABLC параллелограммсӧ. Сідзкӧ, ∆ABC = ∆LCB, SABLC = 2S∆ABC. Татысь артмӧ: S∆ABC = SABLC/2 = ah/2.
Теорема. Трапециялӧн эрдыс лоӧ сылӧн подувъясыс содтасджынлӧн да судтаыслӧн лыдмӧдас.
Эскӧдӧм. Мед ABCD – индӧм трапеция, AD да BC – сылӧн подувъяс, AD = a, BC = b. Мед судтаыс лоӧ h ыджда. Трапецияыс юксьӧ BD диагональӧн ABD да CBD куимпельӧсаяс вылӧ. Сідзкӧ, SABCD = SABD + SCBD = ah/2 + bh/2 = (a + b)h/2.
Пифагор теорема. Веськыдпельӧса куимсэрӧглӧн гипотенуза квадрат ӧтыджда кык катет квадрат содтаскӧд.
Эскӧдӧм. Мед куимсэрӧгыслӧн катетъясыс a да b кузьтаяс, гипотенузаыс c кузьта. Юклам a + b дора квадратсӧ кык ногӧн, кыдзи петкӧдлӧма серпас вылын. Сылӧн эрдыс лоӧ: c2 + 4∙ab/2 = a2 + b2 + 2ab. Сідзкӧ, c2 = a2 + b2.
Кывкӧртӧд. Мед ӧткодь доръяса куимпельӧсалӧн дорыс a кузьта. Сэки сылӧн эрдыс лоӧ S = a2√3/4.
Эскӧдӧм. Нуӧдам куимпельӧсаыслысь судтасӧ. Сійӧ лоӧ медианаӧн. Та вӧсна Пифагор теоремаысь петӧ: судта кузьтаыс лоӧ h = a√3/2. Сідзкӧ, эрдыс лоӧ ah/2 = a2√3/4.
Урчитӧм. Кык мыгӧр ӧтыдждаӧсь, налӧн эрдъясыс кӧ ӧткодьӧсь.
Кывкӧртӧд. Медиана юклӧ куимпельӧсаӧс ӧтыджда кык куимпельӧса вылӧ.
Кывкӧртӧд. Мед CC’ да AB веськыдъяс ӧтнырвизяӧсь. Сэки ABC да ABC’ куимпельӧсаяс ӧтыдждаӧсь.
Кытшвизь
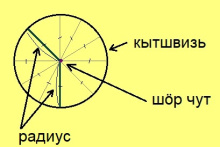
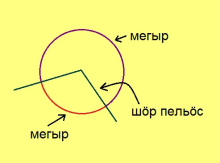
кытшвизь — окружность шӧр чут — центр шӧр пельӧс — центральный угол мегыр — дуга
Тшӧтшкӧсын куйлысь став чут, кодъяс ӧтылнаынӧсь кутшӧмкӧ индӧм чутсяньыс, артмӧдӧны кытшвизь. Тайӧ индӧм чутыс, коді куйлӧ ӧтылнаын кытшвизьса быд чутсяньыс, шуам шӧр чутӧн; ылнаыс кытшвизьсянь шӧр чутӧдзыс шусьӧ радиусӧн.
Кытшвизь шӧр чуткӧд кӧ лӧсялӧ кутшӧмкӧ пельӧслӧн йыв, сэки тайӧ пельӧсыс шусьӧ шӧр пельӧсӧн. Шӧр пельӧс торйӧдӧ кытшвизьсӧ кык юкӧнӧ; тайӧ юкӧнъясыс шусьӧны кытшвизь мегыръясӧн.
Кытшвизь вылын куйлысь кык чутсӧ йитан вундӧг шусьӧ хордаӧн. Шӧр чут пыр мунысь хорда шусьӧ диаметрӧн.
Теорема. Кытшвизьлӧн ӧтыджда шӧр пельӧсъяслы лӧсялӧны ӧтыджда хордаяс.
Подулалӧм. Мед A, B, C, D чутъяс куйлӧны кытшвизь вылын, O — шӧрчут, ∠AOB = ∠COD. Сідзкӧ OA = OB = OC = OD да ∆AOB = ∆COD медводдза тӧдмӧг серти. Та вӧсна AB = CD.
Висьталӧм. Кытшвизьлӧн ӧтыджда хордаяслы лӧсялӧны ӧтыджда шӧр пельӧсъяс.
Эскӧдӧм. Мед A, B, C, D кутъяс куйлӧны кытшвизь вылын, O – шӧрчут, AB = CD. Сідзкӧ, OA = OB = OC = OD да ∆AOB = ∆COD коймӧд тӧдмӧс серти. Та вӧсна ∠AOB = ∠COD.
Висьталӧм. Хордалы ӧшанвизьлуна диаметр юклӧ сійӧс шӧрипӧв.
Эскӧдӧм. Мед AB – хорда, CD – сылы ӧшанвизьлуна диаметр, O – кытшвизьыслӧн шӧрчут, M – хордаыс диаметрыскӧд вомӧнасян чут. Сідзкӧ, O чут куйлӧ CD вылын, OM – AOB куимпельӧсалӧн судта. AO = OB, та вӧсна OM лоӧ AOB куимпельӧсалӧн медиана.
Висьталӧм. Ӧтнырвизя кык хорда костын куйлӧны ӧтыджда шӧр пельӧсъяслы лӧсялана мегыръяс.
Эскӧдӧм. Мед AB да CD – ӧтнырвизя хордаяс. Нуӧдам налы перпендикуляр ногӧн диаметрсӧ; мед сійӧ вомӧнасяс AB-кӧд M чутын, CD-кӧд – N чутын. Сідзкӧ, AM = BM, CN = DN. Мед, шуам, AB ≤ CD. Нуӧдам ABDC трапециялысь AP да BQ судтаяс. Миян артмӧ: CP = DQ. Сідзкӧ, APC да BQD куимпельӧсаяс ӧткодьӧсь кык катет серти. Та вӧсна AC = BD. Тайӧ ӧтыджда мегыръяслы лӧсялӧны ӧтыджда шӧр пельӧсъяс.
Урчитӧм. Мед веськыд визь вомӧнасьӧ кытшвизькӧд; мед вомӧнасян чутӧ гижтӧм радиус да веськыд визьыс ӧшанвизьлунаӧсь. Сэки веськыд визьыс шусьӧ инман веськыдӧн, вомӧнасян чутыс шусьӧ инман чутӧн.
Висьталӧм. Инман веськыд вомӧнасьӧ кытшвизьыскӧд сӧмын ӧти чутын.
Эскӧдӧм. Мед O – кытшвизьыслӧн шӧрчут, A – инман чут, B – веськыд визь вылын куйлысь мӧд чут. Сідзкӧ, AOB – веськыдпельӧса куимсэрӧг, OB – сылӧн гипотенуза. Та вӧсна OB > OA да B чут оз куйлы кытшвизь вылын.
Висьталӧм. Мед кытшвизь вомӧнасьӧ веськыд визькӧд сӧмын ӧти чутын. Сэки найӧ инмӧдчӧны.
Эскӧдӧм. Мед A – кытшвизь веськыд визькӧд вомӧнасян чут, O – кытшвизьыслӧн шӧрчут. Нуӧдам O чутысь веськыд визьлань OB перпендикуляр. B чут кӧ оз лӧсяв A чуткӧд, пуктам веськыд визь вылас C чутсӧ сідз, медым B юкліс AC вундӧгсӧ шӧрипӧв. Миян артмас кык ӧткодь куимпельӧса: OBA да OBC. Сідзкӧ, OC = OA да C лоӧ кытшвизь веськыд визькӧд мӧд вомӧнасян чут.
Висьталӧм. Кытшвизьлӧн да веськыд визьлӧн оз вермы лоны куим ӧтувъя чут.
Эскӧдӧм. Мед O – кытшвизьыслӧн шӧрчут, A – кытшвизьыслӧн да веськыд визьыслӧн вомӧнасян чут, OB – веськыд визьланьыс нуӧдӧм перпендикуляр, R – кытшвизьыслӧн радиус, h – O чутсянь веськыд визьӧдз ылна. Сідзкӧ, OA = R, OB = h, Пифагор теорема серти, AB2 = R2 – h2. Мед A’, A’’ – мӧд да коймӧд вомӧнасян чутъяс. Сэки A’B2 = A’’B2 = R2 – h2. Сідзкӧ, AB = A’B = A’’B; тайӧ оз вермы лоны.
Висьталӧм. Мед кытшвизьлӧн шӧрчутсянь веськыд визьӧдз ылнаыс радиусысь ичӧтджык. Сэки кытшвизьыс вомӧнасьӧ веськыд визьыскӧд кык чутын.
Эскӧдӧм. Мед R – кытшвизьыслӧн радиус, O – кытшвизьыслӧн шӧрчут, OK – веськыд визьланьыс нуӧдӧм перпендикуляр, OK = h. Сідзкӧ, h < R. Мед a2 = R2 – h2. Пуктам веськыд визь вылас K чутсянь кыкнанладорӧ a кузьта вундӧгъяс: AK да BK. Пифагор теорема серти, OA = OB = R. Та вӧсна A да B – кытшвизь веськыд визьыскӧд вомӧнасян чутъяс.
Висьталӧм. Мед кытшвизьлӧн шӧрчутсянь веськыд визьӧдз ылнаыс радиусысь ыджыдджык. Сэки кытшвизьыс веськыд визьыскӧд оз вомӧнась.
Эскӧдӧм. Мед R – кытшвизьыслӧн радиус, O – кытшвизьыслӧн шӧрчут, OK – веськыд визьланьыс нуӧдӧм перпендикуляр, OK = h. Сідзкӧ, h > R. Мед M – веськыд визь вылын куйлысь чут. Пифагор теорема серти, OM > OK > R. Та вӧсна M чут оз куйлы кытшвизь вылын.
Кывкӧртӧд. Кытшвизь вомӧнасьӧ веськыд визькӧд кык чутын сэк да сӧмын сэк, кор шӧрчутсяньыс веськыд визьӧдз ылнаыс радиуссьыс ичӧтджык. Кытшвизь вомӧнасьӧ веськыд визькӧд ӧти чутын сэк да сӧмын сэк, кор шӧрчутсяньыс веськыд визьӧдз ылнаыс радиусыскӧд ӧткодь. Кытшвизь оз вомӧнась веськыд визькӧд да сӧмын сэк, кор шӧрчутсяньыс веськыд визьӧдз ылнаыс радиуссьыс ыджыдджык.
Урчитӧм. Мед унапельӧсалӧн быд йыв куйлӧ кытшвизь вылын. Сэки кытшвизьыс шусьӧ гӧгӧртанаӧн.
Урчитӧм. Мед унапельӧсалӧн быд дор инмӧдчӧ кытшвизькӧд. Сэки кытшвизьыс шусьӧ тӧрӧдчӧмаӧн.
Теорема. Быд куимпельӧсалӧн эм гӧгӧртана кытшвизь.
Эскӧдӧм. Мед ABC – куимпельӧса. Нуӧдам AB да AC вундӧгъяслы шӧр перпендикуляръяс. Найӧ вомӧнасьӧны O чутын. Сэки AO = OB, AO = OC. Сідзкӧ, O – гӧгӧртана кытшвизьлӧн шӧрчут.
Теорема. Куимпельӧсалӧн гӧгӧртана кытшвизь сӧмын ӧти.
Эскӧдӧм. Мед ABC – куимпельӧса, O – гӧгӧртана кытшвизьлӧн шӧрчут. Сэки OA = OB = OC. Та вӧсна O чут куйлӧ AB да AC вундӧгъяслӧн шӧр перпендикуляръяс вылын. Колис казьтыштны: веськыд визьяс вомӧнасьӧны сӧмын ӧти чутын.
Теорема. Быд куимпельӧсалӧн эм тӧрӧдчӧм кытшвизь.
Эскӧдӧм. Мед ABC – индӧм куимпельӧса. Нуӧдам A да B пельӧсъяслысь биссектрисаяссӧ. Найӧ вомӧнасьӧны O чутын. Мед OK, OL, OM – AB, AC да BC вылӧ нуӧдӧм перпендикуляръяс. AO да BO – биссектрисаяс, та вӧсна OK = OL, OK = OM. Сідзкӧ, O – тӧрӧдчӧм кытшвизьлӧн шӧрчут.
Теорема. Куимпельӧсаӧ тӧрӧдчӧм кытшвизь сӧмын ӧти.
Эскӧдӧм. Мед ABC – куимпельӧса, O – тӧрӧдчӧм кытшвизьлӧн шӧрчут, OK, OL, OM – AB, AC да BC-ӧ нуӧдӧм перпендикуляръяс. Сэки OK = OL = OM. Та вӧсна O чут куйлӧ A да B пельӧсъяслӧн биссектрисаяс вылын. Кольӧ казьтыштны: веськыд визьяс вомӧнасьӧны сӧмын ӧти чутын.
Теорема. Куимпельӧсалӧн эрд лоӧ сылӧн периметр джын тӧрӧдчӧм кытшвизьлӧн радиус пӧв лыдмӧдӧм.
Эскӧдӧм. Мед ABC – куимпельӧса, P – сылӧн периметр, O – тӧрӧдчӧм кытшвизьлӧн шӧрчут, r – тӧрӧдчӧм кытшвизьлӧн радиус. Сідзкӧ, SABC = SAOB + SBOC + SAOC = AB∙r/2 + BC∙r/2 + AC∙r/2 = r∙P/2.
Теорема. Ӧти чутысь петысь инман вундӧгъясыс ӧтыдждаӧсь.
Эскӧдӧм. Мед O – кытшвизьлӧн шӧрчут, AB да AC – инман вундӧгъяс (B да C – инман чутъяс). Сэки ABO да ACO куимпельӧсаяс ӧткодьӧсь катет да гипотенуза серти. Сідзкӧ, AB = AC.
Урчитӧм. Мед пельӧслӧн доръясыс вомӧнасьӧны кытшвизькӧд да ӧти вомӧнасян чутыс – пельӧсыслӧн йыв. Сэки тайӧ пельӧсыс шусьӧ тӧрӧдчӧма пельӧсӧн.
Казьтылам: шӧр пельӧс юклӧ кытшвизьсӧ кык мегыр вылӧ. Ӧти мегырыслӧн чутъяс куйлӧны пельӧс доръяс костын. Шуам: тайӧ мегырлӧн ыдждаыс лоӧ шӧр пельӧсыслӧн ыджда. Мӧд мегыр ыдждаыс лоӧ 360° да медводдза мегыр ыджда чинтас.
Висьталӧм. Мед тӧрӧдчӧма пельӧслӧн ӧти дор мунӧ кытшвизьлӧн шӧрчут пырыс. Сэки пельӧсыслӧн ыджда лоӧ сійӧс мыджысь мегыр ыджда джын.
Эскӧдӧм. Мед A – пельӧсыслӧн йыв, B да C – кытшвизькӧд вомӧнасян чутъяс, O – кытшлӧн шӧрчут, AC – диаметр. AOB – ӧткодь берда куимпельӧса. Сідзкӧ, ∠OAB = ∠OBA. ∠BOC лоӧ AOB куимпельӧсалӧн ортсыса пельӧс; та вӧсна ∠BOC = ∠OAB + ∠OBA = 2∠CAB.
Теорема. Тӧрӧдчӧма пельӧслӧн ыджда лоӧ сійӧс мыджысь мегыр ыджда джын.
Эскӧдӧм. Мед A – пельӧсыслӧн йыв, B да C – кытшвизькӧд вомӧнасян чутъяс, O – кытшлӧн шӧрчут. Колӧ петкӧдлыны: ∠BOC = 2∠BAC. Мед AD – диаметр. AD кӧ лӧсялӧ пельӧсыслӧн ӧти доркӧд, ӧткодьлуныс подулалӧма нин. Мед AD мунӧ AB да AC костын. Сэки ∠BOC = ∠BOD + ∠DOC = 2∠BAD + 2∠DAC = 2∠BAC. Мед AD оз мун AB да AC костын. Шуам, AC мунӧ AB да AD костын. Сідзкӧ, ∠BOC = ∠BOD – ∠COD = 2∠BAD – 2∠CAD = 2∠BAC.
Кывкӧртӧд. Тӧрӧдчӧма пельӧс мыджсьӧ диаметр вылӧ сэк да сӧмын сэк, кор сійӧ веськыд.
Кытш сайын чут пыр инман веськыд гижтӧм.
Анализ. Мед O – кытшвизьлӧн шӧрчут, A – кытш сайын куйлысь чут, AB – инман веськыд (B – инман чут). Сэки OBA пельӧс веськыд. Та вӧсна сійӧ тӧрӧдчӧма OA диаметра кытшвизьӧ. Сідзкӧ, B – сетӧм кытшвизь OA диаметра кытшвизькӧд вомӧнасян чут.
Артмӧдӧм. Йитам O да A чутъяс вундӧгӧн, сэсся пуктам сылысь шӧрчутсӧ. Сы бӧрын гижтам OA диаметра кытшвизьсӧ. Сійӧ вомӧнасяс сетӧм кытшвизькӧд кык чутын: B да B’-ын. OB да OB’ лоӧ инман веськыд.
Теорема. Мед куимпельӧсалӧн доръясыс a, b, c кузьтаяс, R – гӧгӧртана кытшвизь радиус, S – куимпельӧса эрдыс. Сэки S = abc/4R.
Эскӧдӧм. Мед AK = h лоӧ BC = a дорӧ гижтӧм судта. Сэки S = ah/2. Сідзкӧ, колӧ петкӧдлыны: h = bc/2R. Мед O – гӧгӧртана кытшвизьлӧн шӧрчут, OH лоӧ AC дорӧ гижтӧм судта. Сэки ∠AOC = 2∠ABC, та вӧсна ∠HOC = ∠ABC; сідзкӧ, HOC да KBA куимпельӧсаяс ӧтсямаӧсь. Миян артмӧ: HC : OC = AK : AB, либӧ h = AK = HC∙AB/OC = bc/2R.
Теорема. Мед пельӧслӧн йыв куйлӧ кытш пытшкын. Сэки сійӧ ыджыдджык сійӧс мыджысь мегыр джынйысь.
Эскӧдӧм. Мед A — пельӧсыслӧн йыв. Мед кытшвизьыс вомӧнасьӧ пельӧсыслӧн доръяскӧд B да C чутъясын. Нюжӧдам AB вундӧгсӧ да артмӧдам веськыд визь. Сійӧ вомӧнасьӧ кытшвизькӧд B да D чутъясын. Миян артмӧ: ∠BDC = 180° – ∠DBC – ∠DCB < 180° – ∠DBC – ∠DCB = ∠BAC. Сідзкӧ, ∠BAC ыджыдджык ∠BDC-ысь, коді лоӧ сійӧс мыджысь мегыр ыджда джын; тайӧ мегырыс мыджӧ и ∠BAC пельӧссӧ.
Теорема. Мед пельӧслӧн йыв куйлӧ кытш ортсыын, кыкнан дорыс вомӧнасьӧ кытшвизьыскӧд. Сэки сійӧ ичӧтджык сійӧс мыджысь мегыр джынйысь.
Эскӧдӧм. Пельӧсыслӧн дор либӧ вомӧнасьӧ кытшвизьыскӧд торъялана кык чутын, либӧ инмӧ сыӧ. Эм кӧ кык вомӧнасян чут, мегыр пом пыдди позьӧ босьтны йывсянь ылынджык куйлысь чутсӧ (сэки мыджысь мегыр ыдждаыс лоас медічӧтӧн). Миян артмӧ кык случай. 1) Пельӧсыслӧн ӧти дор вомӧнасьӧ кытшвизьыскӧд кык чутын. Сэки ∠BDC = 180° – ∠DBC – ∠DCB > 180° – ∠DBC – ∠DCB = ∠BAC. Сідзкӧ, ∠BAC ичӧтджык ∠BDC-ысь, коді лоӧ сійӧс мыджысь мегыр ыджда джын; тайӧ мегырыс мыджӧ и ∠BAC пельӧссӧ. 2) Пельӧсыслӧн кыкнан дор инмӧ кытшвизьӧ. Мед ∠BAC = α. Сэки ∠BOC = 360° – α – 90° – 90° = 180° – α. Сідзкӧ, мыдждыс мегырыс лоӧ 360° – (180° – α) = 180° + α. Кольӧ казявны: α < 180°, та вӧсна α < (180° + α)/2.
Теорема. Нёльпельӧсалӧн кӧ эм гӧгӧртана кытшвизь, сылӧн воча пельӧсъяс суммаыс лоӧ 180°.
Эскӧдӧм. Мед ABCD нёльпельӧсалӧн эм гӧгӧртана кытшвизь. Сэки ∠ABC = ‿ADC/2, ∠ADC = ‿ABC/2; сідзкӧ, ∠ABC + ∠ADC = (‿ADC + ‿ABC)/2 = 360°/2 = 180°.
Теорема (мӧдара). Нёльпельӧсалӧн кӧ воча пельӧсъяс суммаыс лоӧ 180°, сылӧн эм гӧгӧртана кытшвизь.
Эскӧдӧм. Мед ABCD нёльпельӧсалӧн воча пельӧсъяс суммаыс лоӧ 180°. Гижтам ABC‐лысь гӧгӧртана кытшвизьсӧ. D чут кӧ куйлӧ кытш пытшкас, ∠ADC > ‿ABC/2 = 180° – ‿ADC/2 = 180° – ∠ABC; та вӧсна ∠ADC + ∠ABC > 180°. D чут кӧ куйлӧ кытш ортсыас, сэтшӧм жӧ ногӧн артмӧдам: ∠ADC + ∠ABC < 180°. Сідзкӧ, D чут куйлӧ кытшвизь вылын.
Кывкӧртӧд. Параллелограммлӧн эм гӧгӧртана кытшвизь сэк да сӧмын сэк, кор сійӧ лоӧ веськыдсэрӧг.
Эскӧдӧм. Параллелограммлӧн воча пельӧсъясыс ӧтыдждаӧсь. Сідзкӧ, налӧн суммаыс 180° ыджда сэк да сӧмын сэк, кор тайӧ пельӧсъясыс веськыдӧсь.
Кывкӧртӧд. Трапециялӧн эм гӧгӧртана кытшвизь сэк да сӧмын сэк, кор сійӧ ӧткодь берда.
Эскӧдӧм. Трапециялӧн боквыв дор бердса пельӧсъяслӧн суммаыс 180° ыджда. Сідзкӧ, воча пельӧсъяслӧн суммаыс 180° ыджда сэк да сӧмын сэк, кор подувбердса пельӧсъяс ӧтыдждаӧсь (а сідзкӧ, трапецияыс ӧткодь берда).
Теорема. Мед нёльпельӧсалӧн эм тӧрӧдчӧма кытшвизь. Сэки сылӧн воча доръяс суммаясыс ӧткодьӧсь.
Эскӧдӧм. Мед ABCD нёльпельӧсалӧн эм тӧрӧдчӧма кытшвизь. Колӧ петкӧдлыны: AB + CD = BC + DA. Мед K, L, M, N — кытшвизьӧ инман чутъяс. Сэки AK = AN, BK = BL, CL = CM, DM = DN. Сідзкӧ, AB + CD = AK + BK + CM + DM = AN + BL + CM + DN = BC + DA.
Теорема. Мед нёльпельӧсалӧн воча доръяс суммаясыс ӧткодьӧсь. Сэки сылӧн эм тӧрӧдчӧма кытшвизь.
Эскӧдӧм. Мед ABCD нёльпельӧсалӧн AB + CD = BC + DA. Гижтам ∠A да ∠B-лысь биссектрисаяссӧ; налӧн вомӧнасян чутыс лоас шӧрчутӧн кытшвизьлы, коді инмӧ AB, DA да BC доръясӧ. Колӧ петкӧдлыны: CD дор инмӧ тайӧ кытшвизяс. Гижтам C чут пыр кытшвизьыскӧд мӧд инман веськыд визьсӧ. Мед сійӧ вомӧнасьӧ AD веськыд визькӧд D' чутын. Сідзкӧ, ABCD' нёльпельӧсалӧн эм тӧрӧдчӧма кытшвизь; сідзкӧ, AB + CD' = BC + AD'. Та понда CD' + AD = CD + AD'. Мед D' чут куйлӧ A да D костын. Сэки AD = AD' + D'D. Та вӧсна CD = CD' + DD'. Но куимпельӧса ӧткодьтӧмлун серти, CD < CD' + DD'. Артмӧ кыв вожалӧм. D чут кӧ куйлӧ A да D' костын, сэтшӧм жӧ ногӧн петкӧдам: CD' = CD + DD'. Бара кыв вожалӧм артмас. Сідзкӧ, D' = D.
Кывкӧртӧд. Параллелограммлӧн кӧ эм тӧрӧдчӧма кытшвизь, сійӧ лоӧ ромб.
Эскӧдӧм. Параллелограммлӧн воча доръясыс ӧткодьӧсь. Сідзкӧ, воча доръяс суммаясыс кӧ ӧткодьӧсь, параллелограммлӧн став дорыс ӧтыджда. Сідзкӧ, тайӧ ромб.
Кывкӧртӧд. Трапециялӧн кӧ эм тӧрӧдчӧма кытшвизь, сылӧн подувъяс суммаыс ӧтыджда боквыв доръяс суммаыскӧд.
Кывкӧртӧд. Параллелограммлӧн эмӧсь гӧгӧртана да тӧрӧдчӧма кытшвизьяс сэк да сӧмын сэк, кор сійӧ лоӧ квадрат.
Теорема. Мед кытшвизьлӧн хордаяс AB да CD вомӧнасьӧны N чутын. Сэки AN∙NB = CN∙ND.
Эскӧдӧм. ∠ADC да ∠ABC мыджсьӧны ӧти сійӧ жӧ мегыр вылӧ да, найӧ ӧтыдждаӧсь. Сідзи жӧ артмӧ: ∠DAB = ∠DCB. Та вӧсна ADN да CBN куимпельӧсаяс ӧтсямаӧсь да AN : CN = DN : BN, кытысь артмӧ AN∙NB = CN∙ND.
Теорема. Мед кытш ортсыса ӧти чутысь петӧны инман веськыд визь да вундысь. Сэки на костса пельӧс лоӧ инман вундӧг да вундысьлӧн ортсыса юкӧн костса мегырлӧн ыджда джын.
Эскӧдӧм. Мед AB — инман веськыд визь, B — инман чут, AC — вундысьлӧн ортсыса юкӧн, O — кытшвизьлӧн шӧрчут. Мед ∠CBA = α. Сэки ∠OBC = ∠OCB = 90° – α, ∠BOC = 180° – (90° – α) – (90° – α) = 2α.
Теорема. Мед кытш ортсыса ӧти чутысь петӧны инман веськыд визь да вундысь. Сэки инман вундӧг кузьтаыслӧн квадрат лоӧ вундысьлӧн да сылӧн ортсыса юкӧнлӧн кузьтаяс лыдмӧдас.
Эскӧдӧм. Мед AB — инман веськыд визь, B — инман чут, AC — вундысь, AD — сылӧн ортсыса юкӧн. Миянлы колӧ артмӧдны: AB2 = AD∙AC, либӧ AB : AD = AC : AB. Петкӧдлам: BAC да DAB куимпельӧсаяс ӧтсямаӧсь. Налӧн эм ӧтувъя A пельӧс. ∠ACB = ∠DCB = ‿BD/2 = ∠DBA. Сідзкӧ, куимпельӧсаясыс ӧтсямаӧсь медводдза тӧдмӧс серти.
Урчитӧм. Кытшвизьяс шусьӧны ӧткодь шӧраясӧн, налӧн кӧ ӧти сійӧ жӧ шӧрчут.
Урчитӧм. Кытшвизьяс инмӧны, налӧн кӧ эм дзик ӧти ӧтувъя чут. Ӧти кытшвизь кӧ куйлӧ мӧд кытш пытшкын, найӧ шусьӧны пытшкӧссянь инмысь кытшвизьясӧн; мӧдарӧ кӧ, найӧ шусьӧны ортсысянь инмысь кытшвизьясӧн.
Теорема. Кык кытшвизьлӧн оз вермы лоны куим ӧтувъя чут.
Эскӧдӧм. Мед P, Q — кытшвизьясыслӧн шӧрчутъяс, A, B да C — налӧн ӧтувъя чутъяс. Сідзкӧ, PA = PB, QA = QB; та вӧсна PAQ да PBQ куимпельӧсаяс ӧткодьӧсь коймӧд тӧдмӧс серти. Таысь артмӧ: ∠APQ = ∠BPQ. Сідзкӧ, PQ лоӧ AB‐лы перпендикуляр. Сэтшӧм жӧ ногӧн артмӧ: PQ лоӧ AC‐лы перпендикуляр. Та вӧсна A, B, C куйлӧны ӧти веськыд визь вылын. Мед, шуам, C куйлӧ A да B костын. Гижтам P чутысь APC да BPC куимпельӧсаяслысь медианаяссӧ. Найӧ лоӧны сідзжӧ судтаясӧн. Сідзкӧ, P чутысь позьӧ гижтыны кык торъялана перпендикуляр AB веськыд визьлы. Артмӧ кыв вожалӧм.
Теорема. Мед кытшвизьялӧн радиусъясыс R да r ыджда, шӧрчутъяс костын ылнаыс d ыджда, R − r > d. Сэки кытшвизьясыс оз вомӧнасьны; ичӧтджык кытшыс куйлӧ ыджыдджык кытш пытшкын.
Эскӧдӧм. Мед O лоӧ ыджыдджык кытшлӧн шӧрчут, P лоӧ ичӧтджык кытшлӧн шӧрчут, A лоӧ ичӧтджык кытшвизьлӧн кутшӧмкӧ чут. Куимпельӧса ӧткодьтӧмлунысь артмӧ: OA ≤ OP + AP; та вӧсна OA ≤ d + r < R. Сідзкӧ, A чут куйлӧ ыджыдджык кытш пытшкын; ыджыдджык кытшвизь вылын сійӧ оз куйлы.
Теорема. Мед кытшвизьялӧн радиусъясыс R да r ыджда, шӧрчутъяс костын ылнаыс d ыджда, R − r = d. Сэки кытшвизьясыс инмӧны пытшкӧссянь. Налӧн ӧтувъя чут да шӧрчутъясыс куйлӧны ӧти веськыд визь вылын.
Эскӧдӧм. Мед O лоӧ ыджыдджык кытшлӧн шӧрчут, P лоӧ ичӧтджык кытшлӧн шӧрчут, A лоӧ ичӧтджык кытшвизьлӧн кутшӧмкӧ чут. Мед A чут оз куйлы OP веськыд визь вылын. Куимпельӧса ӧткодьтӧмлунысь артмӧ: OA < OP + AP; та вӧсна OA < d + r = R. Сідзкӧ, A чут куйлӧ ыджыдджык кытш пытшкын; ыджыдджык кытшвизь вылын сійӧ оз куйлы. Мед A чут куйлӧ OP веськыд визь вылын. Сэки OA = OP + AP = d + r = R, либӧ OA = |AP − OP| = |r − d| < R.
Теорема. Мед a, b, c — плюса лыдъяс, a ≥ b, a ≥ c, a < b + c. Сэки эм a, b да c доръяса куимпельӧса.
Эскӧдӧм. Мед h лоӧ a кузьта дорӧ гижтӧм судта; мед сійӧ юклӧ подувсӧ x да a − x кузьта вундӧгъяс вылӧ. Сэки h2 = b2 − x2 = c2 − (a − x)2. Татысь артмӧ: x = (a2 + b2 − c2)/2a. Казялам: x > 0. Куимпельӧсасӧ позьӧ артмӧдны, b2 − x2 лыд кӧ плюса. Сідзкӧ, колӧ подулавны b > x ӧткодьтӧмлунсӧ; сійӧ ӧтвына 2ab > a2 + b2 − c2 ӧткодьтӧмлункӧд, либӧ (a − b)2 < c2; колис казьтывны: a > b, a < b + c, та вӧсна (a − b)2 < c2.
Теорема. Мед кытшвизьялӧн радиусъясыс R да r ыджда, r ≤ R, шӧрчутъяс костын ылнаыс d ыджда, R − r < d < R + r. Сэки кытшвизьясыслӧн эм кык ӧтувъя чут.
Эскӧдӧм. Мед P да Q чутъяс — r да R радиуса кытшвизьяслӧн шӧрчутъяс. Миянлы сетӧма: r ≤ R, R < r + d, d < R + r. Сідзкӧ, эм r, R да d доръяса куимпельӧса (AB = d, AC = r, BC = R). Куимпельӧсаяс йылысь аксиома серти, эмӧсь ABC‐кӧд ӧткодь кык куимпельӧса: PQK да PQL, PQ = AB = d, PK = PL = AC = r, QK = QL = BC = R. Сідзкӧ, K да L — кытшвизьясыслӧн вомӧнасян чутъяс.
Теорема. Мед кытшвизьялӧн радиусъясыс R да r ыджда, шӧрчутъяс костын ылнаыс d ыджда, R + r < d. Сэки кытшвизьясыс оз вомӧнасьны; ӧти кытшыс куйлӧ мӧд ортсыас.
Эскӧдӧм. Мед O лоӧ R радиуса кытшлӧн шӧрчут, P лоӧ r радиуса кытшлӧн шӧрчут, A чут куйлӧ r радиуса кытшвизь вылас. Куимпельӧса ӧткодьтӧмлунысь артмӧ: OA ≥ OP − AP; та вӧсна OA ≥ d − r > R. Сідзкӧ, A чут куйлӧ R радиуса кытш ортсыас; R радиуса кытшвизь вылас сійӧ оз куйлы.
Теорема. Мед кытшвизьялӧн радиусъясыс R да r ыджда, шӧрчутъяс костын ылнаыс d ыджда, R + r = d. Сэки кытшвизьясыс инмӧны ортсысянь. Налӧн ӧтувъя чут да шӧрчутъясыс куйлӧны ӧти веськыд визь вылын.
Эскӧдӧм. Мед O лоӧ R радиуса кытшлӧн шӧрчут, P лоӧ r радиуса кытшлӧн шӧрчут, A лоӧ r радиуса кытшвизьлӧн кутшӧмкӧ чут. Мед A чут оз куйлы OP веськыд визь вылын. Куимпельӧса ӧткодьтӧмлунысь артмӧ: OA > OP − AP; та вӧсна OA > d − r = R. Сідзкӧ, A чут куйлӧ R радиуса кытш ортсыас; R радиуса кытшвизь вылын сійӧ оз куйлы. Мед A чут куйлӧ OP веськыд визь вылын. Сэки OA = OP − AP = d − r = R, либӧ OA = AP + OP = r + d > R.
Кывкӧртӧд. Мед R да r радиуса кытшвизьяслӧн шӧрчутъяс костын ылнаыс лоӧ d. 1) Мед d < R − r. Сэки кытшвизьясыс оз вомӧнасьны, ичӧтджык кытш куйлӧ ыджыдджык пытшкас. 2) Мед d = R − r. Сэки кытшвизьясыс инмӧны пытшкӧссянь. 3) Мед R − r < d < R + r. Сэки кытшвизьясыслӧн эм кык ӧтувъя чут. 4) Мед d = R + r. Сэки кытшвизьясыс инмӧны ортсысянь. 5) Мед d > R + r. Сэки кытшвизьясыс оз вомӧнасьны, ӧти кытш куйлӧ мӧд ортсыас.
Кык кытшвизьлы ортсыса инман веськыд визьсӧ гижтӧм. Сетӧма R да r радиуса кытшвизьяс, R ≥ r, d — шӧрчутъяс костас ылна, d ≥ R − r. Колӧ артмӧдны налы ортсыса инман веськыд визьсӧ.
Артмӧдӧм. Мед O да P — R да r радиуса кытшвизьяслӧн шӧрчутъяс. Гижтам P чутсянь O шӧрчута R − r радиуса кытшвизьлы инман веськыдсӧ. Мед Q — инман чут, OQ визьньӧв вомӧнасьӧ R радиуса кытшвизькӧд A чутын. Сэки PQ да AQ — перпендикуляръяс, AQ = r. Артмӧдам PQAB веськыдсэрӧг. Миян артмӧ: BP = r, AB да BP — перпендикуляръяс, AB да AO — перпендикуляръяс. Сідзкӧ, AB — сетӧм кытшвизьясыслы инман веськыд.
Кык кытшвизьлы пытшкӧсса инман веськыд визьсӧ гижтӧм. Сетӧма R да r радиуса кытшвизьяс, d — шӧрчутъяс костас ылна, d ≥ R + r. Колӧ артмӧдны налы пытшкӧсса инман веськыд визьсӧ.
Артмӧдӧм. Мед O да P — R да r радиуса кытшвизьяслӧн шӧрчутъяс. Гижтам P чутсянь O шӧрчута R + r радиуса кытшвизьлы инман веськыдсӧ. Мед Q — инман чут, OQ визьньӧв вомӧнасьӧ R радиуса кытшвизькӧд A чутын. Сэки PQ да AQ — перпендикуляръяс, AQ = r. Артмӧдам PQAB веськыдсэрӧг. Миян артмӧ: BP = r, AB да BP — перпендикуляръяс, AB да AO — перпендикуляръяс. Сідзкӧ, AB — сетӧм кытшвизьясыслы инман веськыд.
Бур унапельӧсаяс
Урчитӧм. Унапельӧса шусьӧ бурӧн, сылӧн кӧ став дорыс ӧтыджда да став пельӧсыс ӧтыджда.
Видлӧг. Бур куимпельӧса — ӧткодь доръяса куимпельӧса; бур нёльпельӧса — квадрат.
Теорема. Бур унапельӧсалӧн эм гӧгӧртана кытшвизь.
Эскӧдӧм. Мед A1A2A3...An — бур унапельӧса. Гижтам A1 да A2 пельӧсъяслысь биссектрисаяс. Найӧ вомӧнасьӧны O чутын. Петкӧдлам: O лоӧ гӧгӧртана кытшвизьыслӧн шӧрчутӧн. Унапельӧсаыс бур да, ∠AnA1A2 = ∠A1A2A3. Сідзкӧ, ∠OA1A2 = ∠OA2A1. Та вӧсна OA1 = OA2. A1A2 = A2A3, та вӧсна OA1A2 да OA2A3 куимпельӧсаяс ӧткодьӧсь медводдза тӧдмӧс серти; сідзкӧ, ∠OA1A2 = ∠OA3A2 да OA3 лоӧ A3 пельӧслӧн биссектрисаӧн, OA2 = OA3. Сэтшӧм жӧ ногӧн артмӧдам: OA3 = OA4 = OA5 = ... = Oan.
Теорема. Бур унапельӧсалӧн эм тӧрӧдчӧм кытшвизь.
Эскӧдӧм. Мед A1A2A3...An — бур унапельӧса, O — гӧгӧртана кытшвизьыслӧн шӧрчут. Петкӧдлам: сійӧ лоӧ тӧрӧдчӧма кытшвизьлӧн шӧрчутӧн. Ми тӧдам: OA1 = OA2 = OA3 = ... = OAn, A1A2 = A2A3 = ... = An−1An. Сідзкӧ, A1OA2, A2OA3, ..., An−1OAn, AnOA1 куимпельӧсаяс ӧткодьӧсь. Та вӧсна O чутсянь гижтӧм судтаясыс ӧтыдждаӧсь.