Пельӧс трисектрисаяс йылысь — различия между версиями
Наста (сёрнитанін | чӧжӧс) (→Позьӧ-ӧ трисектрисаяс артмӧдны циркуль да линейка отсӧгӧн?) |
Наста (сёрнитанін | чӧжӧс) (→Биссектриса да трисектриса) |
||
| (не показано 12 промежуточных версий этого же участника) | |||
| Строка 6: | Строка 6: | ||
видлӧг – пример | видлӧг – пример | ||
кывкӧртӧд – следствие | кывкӧртӧд – следствие | ||
| + | куимпельӧса (куимсэрӧг) – треугольник | ||
| + | ӧткодь доръяса куимпельӧса (куимсэрӧг) – равносторонний треугольник | ||
==Биссектриса да трисектриса== | ==Биссектриса да трисектриса== | ||
| Строка 15: | Строка 17: | ||
[[Файл:Bissektr.jpg|thumb|center|220px|]] | [[Файл:Bissektr.jpg|thumb|center|220px|]] | ||
| − | 2) | + | 2) Куимсэрӧг пельӧсъяслӧн биссектрисаяс вомӧнасьӧны ӧти чутын. |
[[Файл:Bis1.png|thumb|center|220px|]] | [[Файл:Bis1.png|thumb|center|220px|]] | ||
| Строка 27: | Строка 29: | ||
Мӧд ногӧн кӧ шуны, позьӧ-ӧ кутшӧмкӧ пельӧслысь коймӧд юкӧнсӧ торйӧдны? Вочакывсӧ Важ Грецияын на корсьӧмаӧсь. Казьтыштам: циркульӧн позьӧ гижтыны кутшӧмкӧ шӧрчутсянь бӧрйӧм радиуса кытшвизь, а линейкаӧн позьӧ гижтыны бӧрйӧм кык чут пыр веськыд визь. Пельӧслысь коймӧд юкӧн артмӧдӧм вылӧ тайӧ кык тор вӧчӧмыс элладаса математикъяслы эз на вӧв тырмымӧн. | Мӧд ногӧн кӧ шуны, позьӧ-ӧ кутшӧмкӧ пельӧслысь коймӧд юкӧнсӧ торйӧдны? Вочакывсӧ Важ Грецияын на корсьӧмаӧсь. Казьтыштам: циркульӧн позьӧ гижтыны кутшӧмкӧ шӧрчутсянь бӧрйӧм радиуса кытшвизь, а линейкаӧн позьӧ гижтыны бӧрйӧм кык чут пыр веськыд визь. Пельӧслысь коймӧд юкӧн артмӧдӧм вылӧ тайӧ кык тор вӧчӧмыс элладаса математикъяслы эз на вӧв тырмымӧн. | ||
| − | [[Файл:Archimed.jpg|thumb|center| | + | [[Файл:Archimed.jpg|thumb|center|220px|]] |
Вайӧ петкӧдлам, кыдзи ёсь пельӧслысь коймӧд юкӧнсӧ торйӧдӧма Архимед. Линейка вылас водзвыв кык чут пасъям. Сэсся со мый колӧ вӧчны. | Вайӧ петкӧдлам, кыдзи ёсь пельӧслысь коймӧд юкӧнсӧ торйӧдӧма Архимед. Линейка вылас водзвыв кык чут пасъям. Сэсся со мый колӧ вӧчны. | ||
| Строка 36: | Строка 38: | ||
3) Мед пельӧсыслӧн мӧд дор вомӧнасьӧ кытшвизьыскӧд ''A'' чутын. Ньӧжйӧника вешталам да бергӧдам линейкасӧ сідзи, медым сійӧ ''A'' чут пыр муніс, ӧти пасйӧм чут кытшвизь вылӧ веськаліс (''C'' чут), а мӧдыс – веськыд визь вылӧ (''D'' чут). | 3) Мед пельӧсыслӧн мӧд дор вомӧнасьӧ кытшвизьыскӧд ''A'' чутын. Ньӧжйӧника вешталам да бергӧдам линейкасӧ сідзи, медым сійӧ ''A'' чут пыр муніс, ӧти пасйӧм чут кытшвизь вылӧ веськаліс (''C'' чут), а мӧдыс – веськыд визь вылӧ (''D'' чут). | ||
| + | |||
| + | [[Файл:Trisection.png|thumb|center|330px|]] | ||
Миян артмӧ: ''AB'' = ''BC'' = ''CD''. Коді школа геометрия тӧдӧ, вермас артыштны да аддзас: ''CBD'' пельӧс лоӧ ''ABE'' пельӧс коймӧд юкӧн ыджда. | Миян артмӧ: ''AB'' = ''BC'' = ''CD''. Коді школа геометрия тӧдӧ, вермас артыштны да аддзас: ''CBD'' пельӧс лоӧ ''ABE'' пельӧс коймӧд юкӧн ыджда. | ||
| Строка 48: | Строка 52: | ||
Кывкӧртӧд. 10 градуса пельӧс оз позь циркульӧн да линейкаӧн артмӧдны. | Кывкӧртӧд. 10 градуса пельӧс оз позь циркульӧн да линейкаӧн артмӧдны. | ||
| + | |||
| + | ==Куимпельӧсалӧн трисектрисаяс== | ||
| + | |||
| + | 1899 воын Фрэнк Морли петкӧдлӧма: быд куимпельӧса пытшкын орчча трисектрисаяс вомӧнасян чутъясысь артмӧ ӧткодь доръяса куимпельӧса. | ||
| + | |||
| + | [[Файл:Trisector triangle.jpg|thumb|center|330px|]] | ||
| + | |||
| + | Тайӧ теоремасӧ позьӧ уна ногӧн подулавны. Медся дженьыд да кокньыд эскӧдӧмсӧ Джон Конвей лӧсьӧдӧма (сылӧн “Олӧм” ворсӧм йылысь ми [[“Олӧм”_ворсӧм|гижлім]] нин). Идеяыс со кутшӧм. Казьтыштам: быд куимсэрӧгын пельӧсъяслӧн суммаыс 180° лоӧ. Мед ''a'', ''b'', ''c'' – плюса лыдъяс, a + b + c = 60. Сэки эмӧсь со кутшӧм пельӧсъяса куимсэрӧгъяс: | ||
| + | |||
| + | 60°, 60°, 60°; | ||
| + | ''a'' + 60°, ''b'' + 60°, ''c''; | ||
| + | ''a'' + 60°, ''b'', ''c'' + 60°; | ||
| + | ''a'', ''b'' + 60°, ''c'' + 60°; | ||
| + | ''a'' + 120°, ''b'', ''c''; | ||
| + | ''a'', ''b'' + 120°, ''c''; | ||
| + | ''a'', ''b'', ''c'' + 120°. | ||
| + | |||
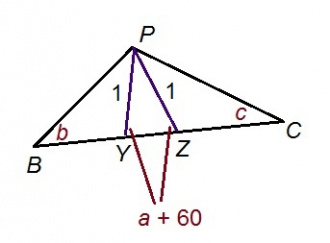
| + | Мед ''BPC'' куимпельӧсалӧн ∠''BPC'' = ''a'' + 120°, ∠''PBC'' = ''b'', ∠''PCB'' = ''c''. Пуктам ''BC'' вылӧ ''Z'' да ''Y'' чутъяс сідзи, медым ∠''PZB'' = ∠''PYC'' = ''a'' + 60°. Нӧшта бӧръям масштаб сідзи, медым ''PZ'' = ''PY'' = 1. Сэки ''BPZ'' куимпельӧсаын ∠''PBZ'' = ''b'', ∠''PZB'' = ''a'' + 60°, ∠''BPZ'' = ''c'' + 60°; ''CPY'' куимпельӧсаын ∠''PCY'' = ''c'', ∠''PYC'' = ''a'' + 60°, ∠''CPY'' = ''b'' + 60°. | ||
| + | |||
| + | [[Файл:Bpc.jpg|thumb|center|330px|]] | ||
| + | |||
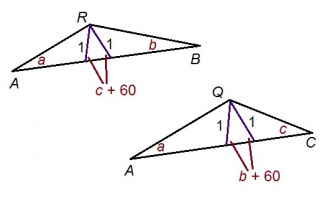
| + | Сэтшӧм жӧ ногӧн артмӧдам ''a'', ''b'', ''c'' + 120° пельӧсъяса ''ARB'' куимсэрӧг да ''a'', ''b'' + 120°, ''c'' пельӧсъяса ''AQC'' куимсэрӧг. | ||
| + | |||
| + | [[Файл:Arb.jpg|thumb|center|330px|]] | ||
| + | |||
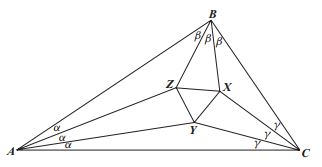
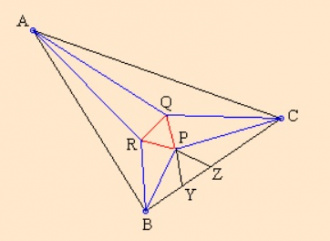
| + | Вӧлӧмкӧ, пуктыны кӧ ∆''BPC'', ∆''ARB'', ∆''AQC'', ∆''BPR'' = ∆''BPZ'', ∆''CPQ'' = ∆''CPY'', кыдзи серпас вылын петкӧдлӧма, артмас 3''a'', 3''b'', 3''c'' пельӧсъяса ''ABC'' куимсэрӧг, сылӧн ''AR'', ''AQ'', ''BP'', ''BR'', ''CP'', ''CQ'' трисектрисаяс да ӧткодь доръяса ''PQR'' куимпельӧса. | ||
| + | |||
| + | [[Файл:Conway proof.jpg|thumb|center|330px|]] | ||
==Пасйӧд== | ==Пасйӧд== | ||
==Содтӧд юӧр== | ==Содтӧд юӧр== | ||
| − | [https://lovziem.blogspot.com/2020/04/1.html Велӧдӧм паськӧдан блогын.] | + | [https://lovziem.blogspot.com/2020/04/1.html Велӧдӧм паськӧдан блогын - 1.] |
| + | [https://lovziem.blogspot.com/2020/04/2.html Велӧдӧм паськӧдан блогын - 1.] | ||
[[Category:Математика]] | [[Category:Математика]] | ||
Текущая версия на 12:59, 4 ода кора 2020
Содержание
Терминъяс
кытшвизь – окружность веськыд визь – прямая тшӧтшкӧс – плоскость плюса дзонь лыд – положительное целое число видлӧг – пример кывкӧртӧд – следствие куимпельӧса (куимсэрӧг) – треугольник ӧткодь доръяса куимпельӧса (куимсэрӧг) – равносторонний треугольник
Биссектриса да трисектриса
Биссектриса юкӧ пельӧссӧ шӧрипӧв. Школа геометрияысь ми тӧдам:
1) Быд пельӧслысь биссектрисасӧ позьӧ вӧчны циркульӧн да линейкаӧн.
2) Куимсэрӧг пельӧсъяслӧн биссектрисаяс вомӧнасьӧны ӧти чутын.
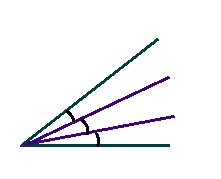
Трисектрисаяс – пельӧссӧ куим пельӧ юкысь кык веськыд визь.
Позьӧ-ӧ трисектрисаяс артмӧдны циркуль да линейка отсӧгӧн?
Мӧд ногӧн кӧ шуны, позьӧ-ӧ кутшӧмкӧ пельӧслысь коймӧд юкӧнсӧ торйӧдны? Вочакывсӧ Важ Грецияын на корсьӧмаӧсь. Казьтыштам: циркульӧн позьӧ гижтыны кутшӧмкӧ шӧрчутсянь бӧрйӧм радиуса кытшвизь, а линейкаӧн позьӧ гижтыны бӧрйӧм кык чут пыр веськыд визь. Пельӧслысь коймӧд юкӧн артмӧдӧм вылӧ тайӧ кык тор вӧчӧмыс элладаса математикъяслы эз на вӧв тырмымӧн.
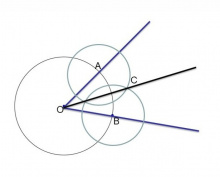
Вайӧ петкӧдлам, кыдзи ёсь пельӧслысь коймӧд юкӧнсӧ торйӧдӧма Архимед. Линейка вылас водзвыв кык чут пасъям. Сэсся со мый колӧ вӧчны.
1) Пельӧслысь ӧти дорсӧ нюжӧдам веськыд визьӧ.
2) Циркульӧн кытшвизь нуӧдам: шӧрчутыс мед лоас пельӧс йылын (B чут), а радиусыс линейка вылас пасйӧм чутъяс кост ыджда.
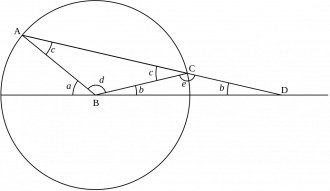
3) Мед пельӧсыслӧн мӧд дор вомӧнасьӧ кытшвизьыскӧд A чутын. Ньӧжйӧника вешталам да бергӧдам линейкасӧ сідзи, медым сійӧ A чут пыр муніс, ӧти пасйӧм чут кытшвизь вылӧ веськаліс (C чут), а мӧдыс – веськыд визь вылӧ (D чут).
Миян артмӧ: AB = BC = CD. Коді школа геометрия тӧдӧ, вермас артыштны да аддзас: CBD пельӧс лоӧ ABE пельӧс коймӧд юкӧн ыджда.
Сідзкӧ, Архимедлы ковмӧма содтӧдтор вӧчны: сэтшӧм ногӧн линейкасӧ пуктыны, медым сійӧ тшӧтшкӧс вылын бӧрйӧм чут пыр муніс, а пасйӧм чутъясыс бӧрйӧм визьясӧ веськалісны.
Позьӧ-ӧ сӧмын веськыд визьяс да кытшвизьяс гижтӧмӧн пельӧслысь артмӧдны трисектрисасӧ? Математикъяс та вылӧ вочакывсӧ уна нэм чӧж корсьӧмаӧсь. И сӧмын 1837-ӧд воын Пьер Ванцель петкӧдлӧма: оз позь.
Дерт, эмӧсь пельӧсъяс, кодъясӧс куим пельӧ юклыны позьӧ циркуль да линейка отсӧгӧн. Шуам, 30 градуса пельӧс позьӧ циркульӧн да линейкаӧн артмӧдны – мӧд ног шуны: веськыд пельӧс позьӧ куим пельӧ юклыны. Вӧлӧмкӧ, 360°/N ыджда пельӧс позьӧ куим пельӧ юклыны сэк да сӧмын сэк, кор N оз юксьы 3 вылӧ (тані N – плюса дзонь лыд).
Видлӧг. 30° = 360°/12; 12 юксьӧ 3 вылӧ. Сідзкӧ, 30 градуса пельӧс циркульӧн да линейкаӧн оз позь куим пельӧ юклыны.
Кывкӧртӧд. 10 градуса пельӧс оз позь циркульӧн да линейкаӧн артмӧдны.
Куимпельӧсалӧн трисектрисаяс
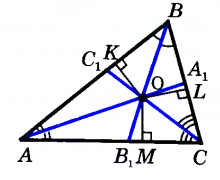
1899 воын Фрэнк Морли петкӧдлӧма: быд куимпельӧса пытшкын орчча трисектрисаяс вомӧнасян чутъясысь артмӧ ӧткодь доръяса куимпельӧса.
Тайӧ теоремасӧ позьӧ уна ногӧн подулавны. Медся дженьыд да кокньыд эскӧдӧмсӧ Джон Конвей лӧсьӧдӧма (сылӧн “Олӧм” ворсӧм йылысь ми гижлім нин). Идеяыс со кутшӧм. Казьтыштам: быд куимсэрӧгын пельӧсъяслӧн суммаыс 180° лоӧ. Мед a, b, c – плюса лыдъяс, a + b + c = 60. Сэки эмӧсь со кутшӧм пельӧсъяса куимсэрӧгъяс:
60°, 60°, 60°; a + 60°, b + 60°, c; a + 60°, b, c + 60°; a, b + 60°, c + 60°; a + 120°, b, c; a, b + 120°, c; a, b, c + 120°.
Мед BPC куимпельӧсалӧн ∠BPC = a + 120°, ∠PBC = b, ∠PCB = c. Пуктам BC вылӧ Z да Y чутъяс сідзи, медым ∠PZB = ∠PYC = a + 60°. Нӧшта бӧръям масштаб сідзи, медым PZ = PY = 1. Сэки BPZ куимпельӧсаын ∠PBZ = b, ∠PZB = a + 60°, ∠BPZ = c + 60°; CPY куимпельӧсаын ∠PCY = c, ∠PYC = a + 60°, ∠CPY = b + 60°.
Сэтшӧм жӧ ногӧн артмӧдам a, b, c + 120° пельӧсъяса ARB куимсэрӧг да a, b + 120°, c пельӧсъяса AQC куимсэрӧг.
Вӧлӧмкӧ, пуктыны кӧ ∆BPC, ∆ARB, ∆AQC, ∆BPR = ∆BPZ, ∆CPQ = ∆CPY, кыдзи серпас вылын петкӧдлӧма, артмас 3a, 3b, 3c пельӧсъяса ABC куимсэрӧг, сылӧн AR, AQ, BP, BR, CP, CQ трисектрисаяс да ӧткодь доръяса PQR куимпельӧса.
Пасйӧд
Содтӧд юӧр
Велӧдӧм паськӧдан блогын - 1. Велӧдӧм паськӧдан блогын - 1.