Майтӧг плёнкаяс чукӧръяс — различия между версиями
Наста (сёрнитанін | чӧжӧс) (→Плато законъяс) |
Наста (сёрнитанін | чӧжӧс) (→Плато законъяс) |
||
| (не показано 6 промежуточных версий этого же участника) | |||
| Строка 14: | Строка 14: | ||
Со кутшӧм аслыспӧлӧслун больк чукӧръяслысь сійӧ казялӧма. | Со кутшӧм аслыспӧлӧслун больк чукӧръяслысь сійӧ казялӧма. | ||
| − | Майтӧг плёнкаяс тэчӧмаӧсь шыльыд веркӧсъясысь. Кутшӧм налӧн формаыс? Кык пример ми тӧдам нин: катеноид да сфера. Вӧлӧмкӧ, оз быд веркӧс вермы лоны майтӧг плёнка юкӧнӧн. | + | '''Майтӧг плёнкаяс тэчӧмаӧсь шыльыд веркӧсъясысь. Кутшӧм налӧн формаыс?''' Кык пример ми тӧдам нин: [[Майтӧг_плёнкаяс_йылысь|катеноид]] да [[Майтӧг_больк|сфера]]. Вӧлӧмкӧ, оз быд веркӧс вермы лоны майтӧг плёнка юкӧнӧн. |
[[Файл:Soap films.jpg|thumb|center|330px|]] | [[Файл:Soap films.jpg|thumb|center|330px|]] | ||
| − | Шыльыд веркӧсса быд чутлӧн эм лыда характеристика — шӧр чукльӧм. Плато аддзӧма: майтӧг плёнкалӧн быд шыльыд юкӧнлӧн шӧр чукльӧм лоӧ константаӧн. Вылыс математикатӧг абу кокньыд шӧр чукльӧм йылысь висьтавны, та вӧсна ми сӧмын некымын пример вайӧдлам: 1) тшӧтшкӧслӧн шӧр чукльӧм лоӧ 0; 2) ''R'' радиуса сфералӧн шӧр чукльӧм лоӧ 1/''R''; 3) катеноидлӧн шӧр чукльӧм лоӧ 0. | + | Шыльыд веркӧсса быд чутлӧн эм лыда характеристика — ''шӧр чукльӧм''. Плато аддзӧма: майтӧг плёнкалӧн быд шыльыд юкӧнлӧн шӧр чукльӧм лоӧ константаӧн. Вылыс математикатӧг абу кокньыд шӧр чукльӧм йылысь висьтавны, та вӧсна ми сӧмын некымын пример вайӧдлам: 1) тшӧтшкӧслӧн шӧр чукльӧм лоӧ 0; 2) ''R'' радиуса сфералӧн шӧр чукльӧм лоӧ 1/''R''; 3) катеноидлӧн шӧр чукльӧм лоӧ 0. |
| − | + | [[Файл:Bolk cuker.jpg|thumb|center|330px|]] | |
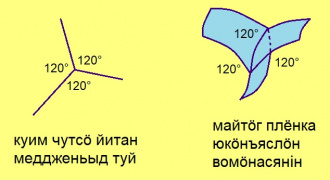
| − | Кыдзи вомӧнасьӧны веркӧс доръясыс? Плато казялӧма: быд вомӧнасян чутысь петӧ нёль дор; тайӧ чукля визьяс костын пельӧсъяс ӧтыдждаӧсь бур тетраэдрлӧн судтаяс костса пельӧскӧд (≈ 109.47°). | + | '''Кыдзи вомӧнасьӧны тайӧ веркӧсъясыс?''' Вӧлӧмкӧ, быд вомӧнасянінысь (чукля визьысь) петӧ куим веркӧс; на костын пельӧсъясыс 120° ыдждаӧсь. Коді лыддис [[Штейнерлӧн_мог|Штейнерлӧн мог]] йылысь, гашкӧ, казьтылас: куим чутӧс йитысь меддженьыд туй кӧ тэчӧма куим вундӧгысь, на костса пельӧсъяс тшӧтш 120° ыдждаӧсь. |
| + | |||
| + | [[Файл:Zadacha steinera i mylnaja plenka.jpg|thumb|center|330px|]] | ||
| + | |||
| + | '''Кыдзи вомӧнасьӧны веркӧс доръясыс?''' Плато казялӧма: быд вомӧнасян чутысь петӧ нёль дор; тайӧ чукля визьяс костын пельӧсъяс ӧтыдждаӧсь бур тетраэдрлӧн судтаяс костса пельӧскӧд (≈ 109.47°). | ||
| + | |||
| + | [[Файл:Soap Bubbles 1.jpg|thumb|center|330px|]] | ||
Математика боксянь Плато законъяссӧ подулалӧма Джин Тэйлор 1976-ӧд воын. | Математика боксянь Плато законъяссӧ подулалӧма Джин Тэйлор 1976-ӧд воын. | ||
| + | |||
| + | [[Файл:Taylor jean.jpg|thumb|center|220px|]] | ||
==Содтӧд юӧр== | ==Содтӧд юӧр== | ||
Текущая версия на 21:02, 9 урасьӧм 2021
Терминъяс
шыльыд веркӧс — гладкая поверхность шӧр чукльӧм — средняя кривизна тшӧтшкӧс — плоскость вундӧг — отрезок
Плато законъяс
Жозеф Плато (1801–1883), Бельгияса математик да физик, нуӧдӧма уна эксперимент майтӧг плёнкаясӧн.
Со кутшӧм аслыспӧлӧслун больк чукӧръяслысь сійӧ казялӧма.
Майтӧг плёнкаяс тэчӧмаӧсь шыльыд веркӧсъясысь. Кутшӧм налӧн формаыс? Кык пример ми тӧдам нин: катеноид да сфера. Вӧлӧмкӧ, оз быд веркӧс вермы лоны майтӧг плёнка юкӧнӧн.
Шыльыд веркӧсса быд чутлӧн эм лыда характеристика — шӧр чукльӧм. Плато аддзӧма: майтӧг плёнкалӧн быд шыльыд юкӧнлӧн шӧр чукльӧм лоӧ константаӧн. Вылыс математикатӧг абу кокньыд шӧр чукльӧм йылысь висьтавны, та вӧсна ми сӧмын некымын пример вайӧдлам: 1) тшӧтшкӧслӧн шӧр чукльӧм лоӧ 0; 2) R радиуса сфералӧн шӧр чукльӧм лоӧ 1/R; 3) катеноидлӧн шӧр чукльӧм лоӧ 0.
Кыдзи вомӧнасьӧны тайӧ веркӧсъясыс? Вӧлӧмкӧ, быд вомӧнасянінысь (чукля визьысь) петӧ куим веркӧс; на костын пельӧсъясыс 120° ыдждаӧсь. Коді лыддис Штейнерлӧн мог йылысь, гашкӧ, казьтылас: куим чутӧс йитысь меддженьыд туй кӧ тэчӧма куим вундӧгысь, на костса пельӧсъяс тшӧтш 120° ыдждаӧсь.
Кыдзи вомӧнасьӧны веркӧс доръясыс? Плато казялӧма: быд вомӧнасян чутысь петӧ нёль дор; тайӧ чукля визьяс костын пельӧсъяс ӧтыдждаӧсь бур тетраэдрлӧн судтаяс костса пельӧскӧд (≈ 109.47°).
Математика боксянь Плато законъяссӧ подулалӧма Джин Тэйлор 1976-ӧд воын.
Содтӧд юӧр
Велӧдӧм паськӧдан блогын.