Лобачевскӧй геометрия — различия между версиями
Наста (сёрнитанін | чӧжӧс) (→Содтӧд юӧр) |
Наста (сёрнитанін | чӧжӧс) (→Куимпельӧсаяс) |
||
| (не показана 51 промежуточная версия этого же участника) | |||
| Строка 4: | Строка 4: | ||
ӧтсяма мыгӧръяс — подобные фигуры | ӧтсяма мыгӧръяс — подобные фигуры | ||
ӧткодь мыгӧръяс — равные фигуры | ӧткодь мыгӧръяс — равные фигуры | ||
| − | кыв вожалӧм — противоречие | + | кыв вожалӧм — противоречие |
| + | визьньӧв — луч | ||
| + | кытшвизь — окружность | ||
| + | абсцисса чӧрс — ось абсцисс | ||
| + | вундӧг — отрезок | ||
| + | инман визьньӧв — касательный луч | ||
| + | воанлыд — предел | ||
| + | тшӧтшкӧс вежлалӧм — преобразование плоскости | ||
| + | тшӧтшкӧс вештӧм — движение плоскости | ||
| + | кык пӧв нюжӧдӧм — растяжение в два раза | ||
| + | параллель ногӧн вештӧм — параллельный перенос | ||
| + | чӧрс — ось | ||
| + | пӧльтӧм — раздутие | ||
| + | плюса лыд — положительное число | ||
| + | куимпельӧса, куимсэрӧг — треугольник | ||
| + | куимпельӧсаяс ӧткодьлун — равенство треугольников | ||
| + | тӧдмалан ног — признак | ||
| + | ӧтсяма куимпельӧсаяс — подобные треугольники | ||
| + | эрд — площадь | ||
==История== | ==История== | ||
| Строка 27: | Строка 45: | ||
Гаусс, Лобачевскӧй да Бойяи куласны пӧшти ӧти кадӧ (1855, 1856 да 1860-ӧд воясӧ). Регыд йӧзӧдасны Гаусслысь гижасьӧмсӧ, выльысь печатайтасны Лобачевскӧйлысь да Бойяилысь уджъяссӧ. 1868-ӧд воын Бельтрами (италияса математик) йӧзӧдас гижӧд Лобачевскӧй тшӧтшкӧслӧн модельяс йылысь. Выль геометрия зумыда пырас математикаӧ. | Гаусс, Лобачевскӧй да Бойяи куласны пӧшти ӧти кадӧ (1855, 1856 да 1860-ӧд воясӧ). Регыд йӧзӧдасны Гаусслысь гижасьӧмсӧ, выльысь печатайтасны Лобачевскӧйлысь да Бойяилысь уджъяссӧ. 1868-ӧд воын Бельтрами (италияса математик) йӧзӧдас гижӧд Лобачевскӧй тшӧтшкӧслӧн модельяс йылысь. Выль геометрия зумыда пырас математикаӧ. | ||
| + | |||
| + | ==Тшӧтшкӧсджынса Пуанкарелӧн модель== | ||
| + | |||
| + | Ӧні петкӧдлам Лобачевскӧйлӧн тшӧтшкӧслысь ӧти модель. Сійӧс вӧзйӧма Эудженио Бельтрами, сёрӧнджык сы йылысь гижлӧма Анри Пуанкаре. Ӧні тайӧ модельсӧ шуӧны тшӧтшкӧсджынса Пуанкарелӧн модельӧн. | ||
| + | |||
| + | ===Тшӧтшкӧс, чутъяс да веськыд визьяс=== | ||
| + | |||
| + | Бӧръям Евклидлӧн тшӧтшкӧс вылын координатаяс система. Лобачевскӧй тшӧтшкӧс пыдди босьтам вылысса тшӧтшкӧсджынсӧ: став (x, y) чутсӧ, кӧні y > 0. Чутъяс пыдди босьтам тайӧ тшӧтшкӧсджын вылас куйлысь чутъяссӧ. Лобачевскӧй тшӧтшкӧсын овлӧны кык сикаса веськыд визьяс: | ||
| + | |||
| + | 1) вертикальногса визьньӧвъяс, кодъяслӧн помыс куйлӧ абсцисса чӧрс вылын, | ||
| + | |||
| + | 2) кытшвизьджынъяс, кодъяслӧн шӧрыс куйлӧ абсцисса чӧрс вылын. | ||
| + | |||
| + | [[Файл:Lob viz.jpg|thumb|center|220px|]] | ||
| + | |||
| + | Пасъям: кутшӧмкӧ чут кӧ оз куйлы Лобачевскӧй тшӧтшкӧсса веськыд визь вылын, тайӧ чут пырыс позьӧ гижтыны веськыд визьыслы помтӧм уна параллель. | ||
| + | |||
| + | [[Файл:Paral1.jpg|thumb|center|220px|]] | ||
| + | |||
| + | [[Файл:Paral2.jpg|thumb|center|220px|]] | ||
| + | |||
| + | ===Кык чут да веськыд визь йылысь аксиома=== | ||
| + | |||
| + | Евклид геометрияысь ми тӧдам аксиома: кык торъялана чут пыр позьӧ гижтыны веськыд визь; татшӧм визьыс овлӧ сӧмын ӧти. Мый позьӧ шуны Лобачесвкӧй тшӧтшкӧсса чутъяс да веськыд визьяс йылысь? Вӧлӧмкӧ, сійӧ жӧ. | ||
| + | |||
| + | 1) Мед кык торъялана чут куйлӧны вертикаль визь вылын. Гижтам тайӧ вертикальсӧ да колям вылысса тшӧтшкӧсджынйын куйлысь юкӧнсӧ. Сійӧ лоас Лобачевскӧй веськыд визьӧн. Некутшӧм мӧд Лобачевскӧй визь оз мун тайӧ чутъяс пырыс: вертикаль визь овлӧ сӧмын ӧти, а кытшвизьлӧн шӧр оз вермы куйлыны абсцисса чӧрс вылын. | ||
| + | |||
| + | [[Файл:2cut1.jpg|thumb|center|220px|]] | ||
| + | |||
| + | 2) Мед кык торъялана чут оз куйлыны вертикаль визь вылын (пасъям найӧс A да B). Сідзкӧ Лобачевскӧй визь вермӧ лоны сӧмын кытшвизьджынйӧн. Артмӧдам сылысь шӧрчутсӧ. Сійӧ лоӧ ӧтылнаын A да B-сянь. Та вӧсна сійӧ куйлӧ AB вундӧглы шӧр перпендикуляр вылын. Нӧшта сійӧ куйлӧ абсцисса чӧрс вылын. Миян артмис: шӧрчутыс лоӧ AB-лы шӧр перпендикулярлӧн да абсцисса чӧрслӧн вомӧнасянінӧн. Тайӧ кык визьыс абу параллельяс да, вомӧнасян чутыс дзик ӧти. | ||
| + | |||
| + | [[Файл:2cut2.jpg|thumb|center|220px|]] | ||
| + | |||
| + | Сідзкӧ и Лобачевскӧй визь (кытшвизьджын) дзик ӧти. | ||
| + | |||
| + | ===Пельӧсъяс да ылнаяс=== | ||
| + | |||
| + | '''Пельӧсъяс мурталӧм.''' Кыдзи ми тӧдам, кык визьньӧвлӧн кӧ помыс ӧтувъя, найӧ артмӧдӧны пельӧс. Лобачевскӧйлӧн тшӧтшкӧсса визьньӧвйӧн лоӧ вертикальногса визьньӧвлӧн юкӧн либӧ кытшвизьджынлӧн мегыр (петкӧдлӧма серпас вылын). | ||
| + | |||
| + | [[Файл:Lob viznev.jpg|thumb|center|220px|]] | ||
| + | |||
| + | Сідзкӧ пельӧссӧ вермӧ артмӧдны 1) кык мегыр, 2) мегыр да вертикаль визьньӧв либӧ вундӧг. | ||
| + | |||
| + | [[Файл:Lob peljes.jpg|thumb|center|220px|]] | ||
| + | |||
| + | Пельӧслысь ыдждасӧ мурталӧны со кыдзи. Йыв пырыс гижтам мегыръясӧ инман визьньӧвъяс. Артмас Евклид геометрияысь пельӧс: сылӧн доръясыс — либӧ кык инман визьньӧв, либӧ ӧти инман визьньӧв да вертикаль визьньӧвлӧн юкӧныс. Тайӧ Евклидлӧн пельӧсыслысь ыдждасӧ и шуам Лобачевскӧйлӧн пельӧсыслӧн ыдждаӧн. | ||
| + | |||
| + | [[Файл:Lob pel murt.jpg|thumb|center|220px|]] | ||
| + | |||
| + | Ӧні гижтам кутшӧмкӧ пельӧс да сылӧн доръяс костӧд мунысь визьньӧв. Позьӧ аддзыны: дзонь пельӧсыс ӧтыджда артмӧм юкӧнъясыслӧн суммакӧд (кыдзи и Евклидлӧн геометрияын). | ||
| + | |||
| + | [[Файл:Lob pel sum.jpg|thumb|center|220px|]] | ||
| + | |||
| + | '''Ылнаяс мурталӧм.''' Кык чут костын ылнасӧ муртавны сьӧкыдджык. Идеяыс со кутшӧм. | ||
| + | |||
| + | Миянлы колӧ артавны ''A'' да ''B'' чутъяс костын ылнасӧ. Гижтам на пырыс Лобачевскӧйлысь веськыд визьсӧ (сійӧ лоас вертикальӧн либӧ кытшвизьджынйӧн). Сідзкӧ ''A'' да ''B'' йитӧма вундӧгӧн либӧ мегырӧн. Пуктам ӧтмоза чутъяссӧ тайӧ вундӧг либӧ мегыр вылас: ''A''₀ = ''A'', ''A''₁, ''A''₂, ''A''₃, ..., ''Aₙ''₋₁, ''Aₙ'' = ''B''. Арталам орчча чутъяс костын Евклид ылнасӧ: ''A''₀''A''₁ вундӧглысь кузьтасӧ пасъям ''s''₁, ''A''₁''A''₂-лысь кузьтасӧ — ''s''₂, да сідз водзӧ. Нӧшта пасъям чутъясыслысь ординатаяссӧ: ''A''₁‐лысь ординатасӧ — ''y''₁, ''A''₂‐лысь — ''y''₂, да с.в. | ||
| + | |||
| + | [[Файл:Lob kuzta.jpg|thumb|center|220px|]] | ||
| + | |||
| + | Ӧні арталам со кутшӧм суммасӧ: | ||
| + | |||
| + | ''Sₙ'' = ''s''₁/''y''₁ + ''s''₂/''y''₂ + ... + ''sₙ''/''yₙ''. | ||
| + | |||
| + | Пондам ыдждӧдны ''n''-сӧ да сьӧрсьӧн-бӧрсьӧн гижам ''Sₙ'' лыдъяссӧ. Вӧлӧмкӧ, налӧн эм воанлыд (пасъям сійӧс ''S'' шыпасӧн): кор ''n'' ыджыд, ''S'' да ''Sₙ'' зэв матынӧсь ӧта-мӧд дорас. Тайӧ ''S'' лыдыс и шусьӧ ''A'' да ''B'' костын ылнаӧн, либӧ ''AB'' вундӧглӧн кузьтаӧн (Лобачевскӧйлӧн тшӧтшкӧс вылын). | ||
| + | |||
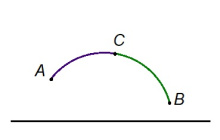
| + | Йитам кӧ A да B чутъяссӧ Лобачевскӧй тшӧтшкӧсса вундӧгӧн да пуктам кӧ сы вылӧ C чутсӧ, артмас: AB‐лӧн кузьтаыс ӧтыджда AC да CB‐лӧн кузьтаяслӧн суммакӧд (кыдзи и Евклидлӧн геометрияын). | ||
| + | |||
| + | [[Файл:Lob kuz sum.jpg|thumb|center|220px|]] | ||
| + | |||
| + | ===Вештӧмъяс=== | ||
| + | |||
| + | Школаын ми велӧдлім Евклид тшӧтшкӧс вежлалӧмъяс да вештӧмъяс йылысь. Казьтыштам, мый сэтшӧмыс вежлалӧм да вештӧм. | ||
| + | |||
| + | Вежлалӧм быд тшӧтшкӧсвывса чутсӧ вуджӧдӧ кутшӧмкӧ тшӧтшкӧсвывса чутӧ. Шуам, горизонталь кузя кык пӧв нюжӧдӧм — тайӧ тшӧтшкӧс вежлалӧм: сійӧ (''x'', ''y'') чутсӧ вуджӧдӧ (2''x'', ''y'') чутӧ. | ||
| + | |||
| + | [[Файл:Vezhlalem.jpg|thumb|center|220px|]] | ||
| + | |||
| + | Тшӧтшкӧс вежлалӧм кӧ оз веж чутъяс костын ылнасӧ, сійӧс шуӧны тшӧтшкӧс вештӧмӧн. Со куим пример. | ||
| + | |||
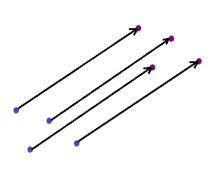
| + | 1. Параллель ногӧн вештӧм (''x'', ''y'') чутсӧ вуджӧдӧ (''x'' + ''a'', ''y'' + ''b'') чутӧ. | ||
| + | |||
| + | [[Файл:Paral vestem.jpg|thumb|center|220px|]] | ||
| + | |||
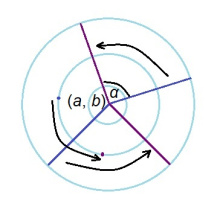
| + | 2. (''a'', ''b'') чут гӧгӧр ''α'' пельӧс вылӧ бергӧдлӧм. | ||
| + | |||
| + | [[Файл:Bergedlem.jpg|thumb|center|220px|]] | ||
| + | |||
| + | 3. Веськыд визь серти симметрия. | ||
| + | |||
| + | [[Файл:Symmetry.jpg|thumb|center|220px|]] | ||
| + | |||
| + | Вӧлӧмкӧ, Евклид тшӧтшкӧс быд вештӧмсӧ позьӧ артмӧдны тадзи: медводз вӧчны параллель ногӧн вештӧм, сэсся (0, 0) чут гӧгӧр бергӧдлӧм; ковмас кӧ, нӧшта сы бӧрын вӧчны абсцисса чӧрс серти симметрия. | ||
| + | |||
| + | Ӧні висьталам Лобачевскӧй тшӧтшкӧс вештӧмъяс йылысь (ылна мурталӧм йылысь ми гижлім нин). Пондам видлавны тшӧтшкӧсджынса Пуанкаре модельсӧ. Медводз вайӧдам некымын пример. | ||
| + | |||
| + | 1. Горизонталь ногӧн вештӧм (''x'', ''y'') чутсӧ вуджӧдӧ (''x'' + ''a'', ''y'') чутӧ. | ||
| + | |||
| + | [[Файл:Goriz vestem.jpg|thumb|center|220px|]] | ||
| + | |||
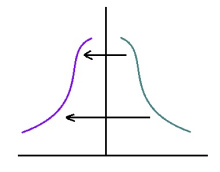
| + | 2. Ордината чӧрс серти симметрия (''x'', ''y'') чутсӧ вуджӧдӧ (−''x'', ''y'') чутӧ. | ||
| + | |||
| + | [[Файл:Y sym.jpg|thumb|center|220px|]] | ||
| + | |||
| + | 3. ''a'' пӧв пӧльтӧм (гомотетия) (''x'', ''y'') чутсӧ вуджӧдӧ (''ax'', ''ay'') чутӧ (тані ''a'' — плюса лыд). | ||
| + | |||
| + | [[Файл:Dilatation1.jpg|thumb|center|220px|]] | ||
| + | |||
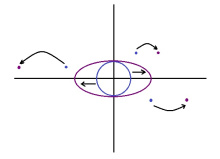
| + | 4. нуль шӧрчута ӧтик радиуса кытшвизь серти инверсия (''x'', ''y'') чутсӧ вуджӧдӧ (''x''/''r''², ''y''/''r''²) чутӧ, кӧні ''r''² = ''x''² + ''y''². Пасъям: кытшвизьвывса быд чут оз вешйы; кытш пытшкын куйлысь чутъяс вуджӧны кытш ортсыӧ, а кытш ортсыын куйлысь чутъяс вуджӧны кытш пытшкӧ. | ||
| + | |||
| + | [[Файл:Inversia.jpg|thumb|center|220px|]] | ||
| + | |||
| + | Вӧлӧмкӧ, Лобачевскӧй тшӧтшкӧс быд вештӧм лоӧ тайӧ нёль вештӧмсьыс кутшӧмкӧ комбинацияӧн (шуам, медводз вӧчсьӧ горизонталь ногӧн вештӧм, сэсся пӧльтӧм, сэсся инверсия; либӧ медводз вӧчсьӧ инверсия, сэсся ордината чӧрс серти симметрия, сэсся горизонталь ногӧн вештӧм). | ||
| + | |||
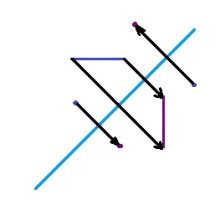
| + | Лобачевскӧй тшӧтшкӧс вештӧмъяс вуджӧдӧны быд веськыд визьсӧ (вертикальсӧ либӧ кытшвизьджынсӧ) веськыд визьӧ — Евклид тшӧтшкӧс вештӧмъяс моз. (Серпас вылас петкӧдлӧма, кытчӧ инверсия вуджӧдӧ веськыд визьяссӧ.) | ||
| + | |||
| + | [[Файл:Inv viz.jpg|thumb|center|220px|]] | ||
| + | |||
| + | ===Куимпельӧсаяс=== | ||
| + | Ӧні ми висьталам Лобачевскӧй тшӧтшкӧсса куимпельӧсаяс йылысь. | ||
| + | |||
| + | Кыдзи ми тӧдам нин, веськыд визьясӧн лоӧны либӧ вертикальногса визьньӧвъяс (налӧн помыс куйлӧ абсцисса чӧрс вылын), либӧ кытшвизьджынъяс (налӧн шӧрыс куйлӧ абсцисса чӧрс вылын). Сідзкӧ, куимпельӧсалӧн доръясыс — либӧ вертикальногса вундӧгъяс, либӧ кытшвизьясыслӧн мегыръяс. | ||
| + | |||
| + | [[Файл:Lob kujimpel.jpg|thumb|center|220px|]] | ||
| + | |||
| + | Ӧткодьлун тӧдмалан ногъяс. Школаын ми велӧдлім куимпельӧсаяслысь ӧткодьлунсӧ куим тӧдмалан ног: | ||
| + | |||
| + | 1) кык дор да на костса пельӧс серти, | ||
| + | |||
| + | 2) ӧти дор да сы бердса кык пельӧс серти, | ||
| + | |||
| + | 3) куим дор серти. | ||
| + | |||
| + | [[Файл:3todm.jpg|thumb|center|220px|]] | ||
| + | |||
| + | Тайӧ теоремаяссӧ подулалігӧн параллельяс йылысь аксиома оз ков. Евклид геометрияысь Лобачевскӧй геометрияын кольӧ став аксиомаыс, параллель йылысь кындзи. Сідзкӧ, и тайӧ куим тӧдмалан ногыс кольӧ. | ||
| + | |||
| + | Вӧлӧмкӧ, Лобачевскӧй геометрияын куимпельӧсаяс ӧткодьлунлӧн эм нӧшта ӧти тӧдмалан ног: | ||
| + | |||
| + | 4) куим пельӧс серти. | ||
| + | |||
| + | '''Теорема.''' Кор ABC да ''A’B’C’'' – куимпельӧсаяс, ∠''A'' = ∠''A’'', ∠''B'' = ∠''B’'', ∠''C'' = ∠''C’'', сэки ∆''ABC'' = ∆''A’B’C’''. | ||
| + | |||
| + | [[Файл:Lob otk kuimp.jpg|thumb|center|220px|]] | ||
| + | |||
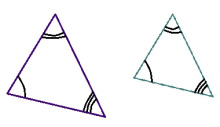
| + | Евклид геометрияын татшӧм куимпельӧсаясыс сӧмын ӧтсямаӧсь, вермӧны лоны оз ӧткодьӧн. | ||
| + | |||
| + | [[Файл:Otsjama eucl1.jpg|thumb|center|220px|]] | ||
| + | |||
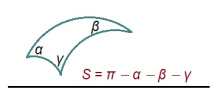
| + | Куимсэрӧглӧн эрд да пельӧсъяслӧн сумма. Сідзкӧ, Лобачевскӧй куимсэрӧгъяслысь ӧткодьлунсӧ позьӧ тӧдмавны сӧмын налӧн пельӧсъяс серти. Ӧткодь куимпельӧсаяслӧн эрдъясыс ӧткодьӧсь жӧ. Гашкӧ, позьӧ гижны кутшӧмкӧ формула куимсэрӧглӧн эрдлы, кытчӧ пырӧны сӧмын пельӧсъясыс? Вӧлӧмкӧ, позьӧ — и тайӧ формулаыс зэв кокньыд. Пондам кӧ муртавны пельӧсъяссӧ радианъясӧн, куимсэрӧглӧн эрдыс лоӧ | ||
| + | |||
| + | ''S'' = ''π'' − ''α'' − ''β'' − ''γ'' | ||
| + | |||
| + | (кӧні ''α'', ''β'', ''γ'' — куимсэрӧгыслӧн пельӧсъяс; π радиан лоӧ 180°). | ||
| + | |||
| + | [[Файл:Lob erd.jpg|thumb|center|220px|]] | ||
| + | |||
| + | Сідзкӧ, Лобачевскӧй куимсэрӧглӧн пельӧсъяслӧн суммаыс пыр лоӧ ''π'' радианысь (либӧ 180°-ысь) этшаджык. Евклид куимсэрӧглӧн тайӧ суммаыс пыр лоӧ 180° ыджда. | ||
| + | |||
| + | '''Пифагорлӧн теорема.''' Евклид геометрияысь ми тӧдам: веськыдпельӧса куимсэрӧглӧн кӧ катетъясыс ''a'' да ''b'' кузьтаӧсь, а гипотенузаыс ''c'' кузьта, сэки ''a''² + ''b''² = ''c''². | ||
| + | |||
| + | Лобачевскӧй геометрияын эм Пифагор теоремалы аналог. Формулаыс со кутшӧм: | ||
| + | |||
| + | ch ''c'' = ch ''a'' ⋅ ch ''b'', | ||
| + | |||
| + | кӧні ''a'', ''b'' — катетъяс, ''c'' — гипотенуза, ch — гипербола косинус (сы йылысь ми коркӧ висьтавлім [[чеп визь]] йылысь гижӧдын). | ||
==Содтӧд юӧр== | ==Содтӧд юӧр== | ||
[https://lovziem.blogspot.com/2022/05/1.html Велӧдӧм паськӧдан блогын − 1.] | [https://lovziem.blogspot.com/2022/05/1.html Велӧдӧм паськӧдан блогын − 1.] | ||
| + | |||
[https://lovziem.blogspot.com/2022/05/2.html Велӧдӧм паськӧдан блогын − 2.] | [https://lovziem.blogspot.com/2022/05/2.html Велӧдӧм паськӧдан блогын − 2.] | ||
| + | |||
| + | [https://lovziem.blogspot.com/2022/05/3.html Велӧдӧм паськӧдан блогын − 3.] | ||
| + | |||
| + | [https://lovziem.blogspot.com/2022/05/4.html Велӧдӧм паськӧдан блогын − 4.] | ||
| + | |||
| + | [https://lovziem.blogspot.com/2022/05/5.html Велӧдӧм паськӧдан блогын − 5.] | ||
[[Category:Математика]] | [[Category:Математика]] | ||
Текущая версия на 01:48, 6 йирым 2022
Содержание
Терминъяс
тшӧтшкӧс — плоскость веськыдсэрӧг — прямоугольник ӧтсяма мыгӧръяс — подобные фигуры ӧткодь мыгӧръяс — равные фигуры кыв вожалӧм — противоречие визьньӧв — луч кытшвизь — окружность абсцисса чӧрс — ось абсцисс вундӧг — отрезок инман визьньӧв — касательный луч воанлыд — предел тшӧтшкӧс вежлалӧм — преобразование плоскости тшӧтшкӧс вештӧм — движение плоскости кык пӧв нюжӧдӧм — растяжение в два раза параллель ногӧн вештӧм — параллельный перенос чӧрс — ось пӧльтӧм — раздутие плюса лыд — положительное число куимпельӧса, куимсэрӧг — треугольник куимпельӧсаяс ӧткодьлун — равенство треугольников тӧдмалан ног — признак ӧтсяма куимпельӧсаяс — подобные треугольники эрд — площадь
История
Школа планиметрияысь ми тӧдам со кутшӧм аксиома: чутыс кӧ оз куйлы веськыд визь вылын, татшӧм чут пырыс оз позь гижтыны тайӧ веськыд визьыслы кык торъялана параллель. Тайӧ аксиомасӧ шуӧны параллельяс йылысь аксиомаӧн либӧ Евклидлӧн 5-ӧд постулатӧн. (Казьтыштам: тшӧтшкӧс вылын кык веськыд визь шусьӧны параллельясӧн, найӧ кӧ оз вомӧнасьны.)
Уна нэм чӧж математикъяс зільӧмаӧсь подулавны тайӧ постулатсӧ. Сӧмын найӧ ставыс вӧдитчӧмаӧсь кутшӧмкӧ содтӧд фактӧн. Шуам, Герсонидлӧн подулалӧмас вӧлі веськыдсэрӧг — но мыйла тшӧтшкӧс вылас быть лоны кӧть ӧти веськыдсэрӧглы? Кутшӧм аксиомаысь тайӧ петӧ? (Герсонид — шӧр нэмъяса туялысь-универсал — математик, астроном, философ, Талмуд тӧдысь; олӧма Францияын.) Валлислӧн вӧліны абу ӧткодь, но ӧтсяма кык мыгӧр (налӧн формаыс ӧти сійӧ жӧ, но ыдждаыс торъя). 18-ӧд нэмын математикъяс видлалӧмаӧсь подулавны параллельяс йылысь аксиомасӧ паныдсянь (от противного), но кыв вожалӧмыс налӧн некыдз эз артмы.
19-ӧд нэмын лои гӧгӧрвоана: позьӧ артмӧдны "абу Евклидлӧн" геометрия (кӧні кольӧ став аксиома, 5-ӧд постулатысь кындзи). Тайӧ геометриясӧ лӧсьӧдӧмаӧсь куим морт: Николай Иванович Лобачевскӧй (медводдза гижӧдыс петӧма 1829-ӧд воын), Янош Бойяи (мадьяр математик; гижӧдыс геометрия кузя петӧма 1832-ӧд воын) да Карл Фридрих Гаусс.
Гаусс ассьыс теориясӧ сӧвмӧдӧма гусьӧн, ньӧти гижӧд "абу Евклидлӧн" геометрия йылысь абу йӧзӧдӧма: чайтӧма, уджъёртъясыс оз гӧгӧрвоны сійӧс.
Вӧлӧмкӧ, Лобачевскӧйкӧд сідзи и лоӧма: сылысь теориясӧ зэв чорыда видӧмаӧсь (увгысьяс пӧвстын вӧлі М. В. Остроградскӧй). Сэсся Лобачевскӧй йӧзӧдӧма ассьыс гижӧдъяссӧ суйӧрсайса журналъясын. Гаусс тӧдмасьӧма сылӧн статьяясыскӧд, ёна найӧс ошкӧма ёрткостса гижасьӧмын да рекомендация сетӧма, медым Лобачевскӧйӧс босьтӧмаӧсь Гёттингенса королевскӧй туялысь котырӧ. Тайӧ ошкӧмыс сылы абу ёна отсалӧма. Нималана математикӧн олӧм дырйиыс Лобачевскӧй абу лоӧма — ни Россияын, ни суйӧр сайын.
Янош Бойяилы уджыс тшӧтш нинӧм эз вай, дзоньвидзалун торксьӧмысь кындзи. Сылӧн батьыс, Фаркаш Бойяи, ыстӧма Гаусслы "абу Евклид" геометрия йылысь гижӧдсӧ. Гаусс уджсӧ бара ёна ошкӧма ёртъясыскӧд гижасьӧмӧн, налы шуӧма — том мортыс пӧ гений, но Бойяияслы вочавидзӧма: став идеяыс пӧ менам идеяяскӧд лӧсялӧ, ме пӧ важӧн нин тайӧ тема кузя мӧвпала. Янош Бойяи шогӧ зэв ёна усьӧма; дзик нин забеднӧ сылы лоӧма, кор сійӧ тӧдмалӧма Лобачевскӧйлӧн гижӧдъяс йылысь.
Гаусс, Лобачевскӧй да Бойяи куласны пӧшти ӧти кадӧ (1855, 1856 да 1860-ӧд воясӧ). Регыд йӧзӧдасны Гаусслысь гижасьӧмсӧ, выльысь печатайтасны Лобачевскӧйлысь да Бойяилысь уджъяссӧ. 1868-ӧд воын Бельтрами (италияса математик) йӧзӧдас гижӧд Лобачевскӧй тшӧтшкӧслӧн модельяс йылысь. Выль геометрия зумыда пырас математикаӧ.
Тшӧтшкӧсджынса Пуанкарелӧн модель
Ӧні петкӧдлам Лобачевскӧйлӧн тшӧтшкӧслысь ӧти модель. Сійӧс вӧзйӧма Эудженио Бельтрами, сёрӧнджык сы йылысь гижлӧма Анри Пуанкаре. Ӧні тайӧ модельсӧ шуӧны тшӧтшкӧсджынса Пуанкарелӧн модельӧн.
Тшӧтшкӧс, чутъяс да веськыд визьяс
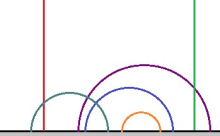
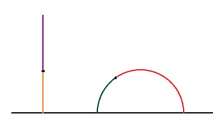
Бӧръям Евклидлӧн тшӧтшкӧс вылын координатаяс система. Лобачевскӧй тшӧтшкӧс пыдди босьтам вылысса тшӧтшкӧсджынсӧ: став (x, y) чутсӧ, кӧні y > 0. Чутъяс пыдди босьтам тайӧ тшӧтшкӧсджын вылас куйлысь чутъяссӧ. Лобачевскӧй тшӧтшкӧсын овлӧны кык сикаса веськыд визьяс:
1) вертикальногса визьньӧвъяс, кодъяслӧн помыс куйлӧ абсцисса чӧрс вылын,
2) кытшвизьджынъяс, кодъяслӧн шӧрыс куйлӧ абсцисса чӧрс вылын.
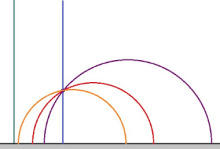
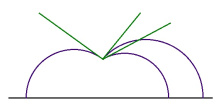
Пасъям: кутшӧмкӧ чут кӧ оз куйлы Лобачевскӧй тшӧтшкӧсса веськыд визь вылын, тайӧ чут пырыс позьӧ гижтыны веськыд визьыслы помтӧм уна параллель.
Кык чут да веськыд визь йылысь аксиома
Евклид геометрияысь ми тӧдам аксиома: кык торъялана чут пыр позьӧ гижтыны веськыд визь; татшӧм визьыс овлӧ сӧмын ӧти. Мый позьӧ шуны Лобачесвкӧй тшӧтшкӧсса чутъяс да веськыд визьяс йылысь? Вӧлӧмкӧ, сійӧ жӧ.
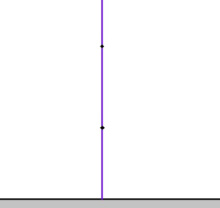
1) Мед кык торъялана чут куйлӧны вертикаль визь вылын. Гижтам тайӧ вертикальсӧ да колям вылысса тшӧтшкӧсджынйын куйлысь юкӧнсӧ. Сійӧ лоас Лобачевскӧй веськыд визьӧн. Некутшӧм мӧд Лобачевскӧй визь оз мун тайӧ чутъяс пырыс: вертикаль визь овлӧ сӧмын ӧти, а кытшвизьлӧн шӧр оз вермы куйлыны абсцисса чӧрс вылын.
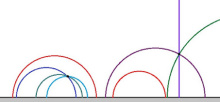
2) Мед кык торъялана чут оз куйлыны вертикаль визь вылын (пасъям найӧс A да B). Сідзкӧ Лобачевскӧй визь вермӧ лоны сӧмын кытшвизьджынйӧн. Артмӧдам сылысь шӧрчутсӧ. Сійӧ лоӧ ӧтылнаын A да B-сянь. Та вӧсна сійӧ куйлӧ AB вундӧглы шӧр перпендикуляр вылын. Нӧшта сійӧ куйлӧ абсцисса чӧрс вылын. Миян артмис: шӧрчутыс лоӧ AB-лы шӧр перпендикулярлӧн да абсцисса чӧрслӧн вомӧнасянінӧн. Тайӧ кык визьыс абу параллельяс да, вомӧнасян чутыс дзик ӧти.
Сідзкӧ и Лобачевскӧй визь (кытшвизьджын) дзик ӧти.
Пельӧсъяс да ылнаяс
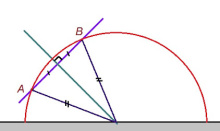
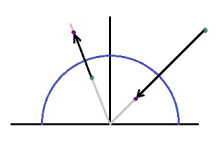
Пельӧсъяс мурталӧм. Кыдзи ми тӧдам, кык визьньӧвлӧн кӧ помыс ӧтувъя, найӧ артмӧдӧны пельӧс. Лобачевскӧйлӧн тшӧтшкӧсса визьньӧвйӧн лоӧ вертикальногса визьньӧвлӧн юкӧн либӧ кытшвизьджынлӧн мегыр (петкӧдлӧма серпас вылын).
Сідзкӧ пельӧссӧ вермӧ артмӧдны 1) кык мегыр, 2) мегыр да вертикаль визьньӧв либӧ вундӧг.
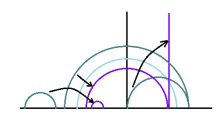
Пельӧслысь ыдждасӧ мурталӧны со кыдзи. Йыв пырыс гижтам мегыръясӧ инман визьньӧвъяс. Артмас Евклид геометрияысь пельӧс: сылӧн доръясыс — либӧ кык инман визьньӧв, либӧ ӧти инман визьньӧв да вертикаль визьньӧвлӧн юкӧныс. Тайӧ Евклидлӧн пельӧсыслысь ыдждасӧ и шуам Лобачевскӧйлӧн пельӧсыслӧн ыдждаӧн.
Ӧні гижтам кутшӧмкӧ пельӧс да сылӧн доръяс костӧд мунысь визьньӧв. Позьӧ аддзыны: дзонь пельӧсыс ӧтыджда артмӧм юкӧнъясыслӧн суммакӧд (кыдзи и Евклидлӧн геометрияын).
Ылнаяс мурталӧм. Кык чут костын ылнасӧ муртавны сьӧкыдджык. Идеяыс со кутшӧм.
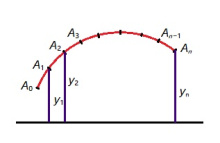
Миянлы колӧ артавны A да B чутъяс костын ылнасӧ. Гижтам на пырыс Лобачевскӧйлысь веськыд визьсӧ (сійӧ лоас вертикальӧн либӧ кытшвизьджынйӧн). Сідзкӧ A да B йитӧма вундӧгӧн либӧ мегырӧн. Пуктам ӧтмоза чутъяссӧ тайӧ вундӧг либӧ мегыр вылас: A₀ = A, A₁, A₂, A₃, ..., Aₙ₋₁, Aₙ = B. Арталам орчча чутъяс костын Евклид ылнасӧ: A₀A₁ вундӧглысь кузьтасӧ пасъям s₁, A₁A₂-лысь кузьтасӧ — s₂, да сідз водзӧ. Нӧшта пасъям чутъясыслысь ординатаяссӧ: A₁‐лысь ординатасӧ — y₁, A₂‐лысь — y₂, да с.в.
Ӧні арталам со кутшӧм суммасӧ:
Sₙ = s₁/y₁ + s₂/y₂ + ... + sₙ/yₙ.
Пондам ыдждӧдны n-сӧ да сьӧрсьӧн-бӧрсьӧн гижам Sₙ лыдъяссӧ. Вӧлӧмкӧ, налӧн эм воанлыд (пасъям сійӧс S шыпасӧн): кор n ыджыд, S да Sₙ зэв матынӧсь ӧта-мӧд дорас. Тайӧ S лыдыс и шусьӧ A да B костын ылнаӧн, либӧ AB вундӧглӧн кузьтаӧн (Лобачевскӧйлӧн тшӧтшкӧс вылын).
Йитам кӧ A да B чутъяссӧ Лобачевскӧй тшӧтшкӧсса вундӧгӧн да пуктам кӧ сы вылӧ C чутсӧ, артмас: AB‐лӧн кузьтаыс ӧтыджда AC да CB‐лӧн кузьтаяслӧн суммакӧд (кыдзи и Евклидлӧн геометрияын).
Вештӧмъяс
Школаын ми велӧдлім Евклид тшӧтшкӧс вежлалӧмъяс да вештӧмъяс йылысь. Казьтыштам, мый сэтшӧмыс вежлалӧм да вештӧм.
Вежлалӧм быд тшӧтшкӧсвывса чутсӧ вуджӧдӧ кутшӧмкӧ тшӧтшкӧсвывса чутӧ. Шуам, горизонталь кузя кык пӧв нюжӧдӧм — тайӧ тшӧтшкӧс вежлалӧм: сійӧ (x, y) чутсӧ вуджӧдӧ (2x, y) чутӧ.
Тшӧтшкӧс вежлалӧм кӧ оз веж чутъяс костын ылнасӧ, сійӧс шуӧны тшӧтшкӧс вештӧмӧн. Со куим пример.
1. Параллель ногӧн вештӧм (x, y) чутсӧ вуджӧдӧ (x + a, y + b) чутӧ.
2. (a, b) чут гӧгӧр α пельӧс вылӧ бергӧдлӧм.
3. Веськыд визь серти симметрия.
Вӧлӧмкӧ, Евклид тшӧтшкӧс быд вештӧмсӧ позьӧ артмӧдны тадзи: медводз вӧчны параллель ногӧн вештӧм, сэсся (0, 0) чут гӧгӧр бергӧдлӧм; ковмас кӧ, нӧшта сы бӧрын вӧчны абсцисса чӧрс серти симметрия.
Ӧні висьталам Лобачевскӧй тшӧтшкӧс вештӧмъяс йылысь (ылна мурталӧм йылысь ми гижлім нин). Пондам видлавны тшӧтшкӧсджынса Пуанкаре модельсӧ. Медводз вайӧдам некымын пример.
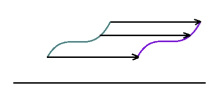
1. Горизонталь ногӧн вештӧм (x, y) чутсӧ вуджӧдӧ (x + a, y) чутӧ.
2. Ордината чӧрс серти симметрия (x, y) чутсӧ вуджӧдӧ (−x, y) чутӧ.
3. a пӧв пӧльтӧм (гомотетия) (x, y) чутсӧ вуджӧдӧ (ax, ay) чутӧ (тані a — плюса лыд).
4. нуль шӧрчута ӧтик радиуса кытшвизь серти инверсия (x, y) чутсӧ вуджӧдӧ (x/r², y/r²) чутӧ, кӧні r² = x² + y². Пасъям: кытшвизьвывса быд чут оз вешйы; кытш пытшкын куйлысь чутъяс вуджӧны кытш ортсыӧ, а кытш ортсыын куйлысь чутъяс вуджӧны кытш пытшкӧ.
Вӧлӧмкӧ, Лобачевскӧй тшӧтшкӧс быд вештӧм лоӧ тайӧ нёль вештӧмсьыс кутшӧмкӧ комбинацияӧн (шуам, медводз вӧчсьӧ горизонталь ногӧн вештӧм, сэсся пӧльтӧм, сэсся инверсия; либӧ медводз вӧчсьӧ инверсия, сэсся ордината чӧрс серти симметрия, сэсся горизонталь ногӧн вештӧм).
Лобачевскӧй тшӧтшкӧс вештӧмъяс вуджӧдӧны быд веськыд визьсӧ (вертикальсӧ либӧ кытшвизьджынсӧ) веськыд визьӧ — Евклид тшӧтшкӧс вештӧмъяс моз. (Серпас вылас петкӧдлӧма, кытчӧ инверсия вуджӧдӧ веськыд визьяссӧ.)
Куимпельӧсаяс
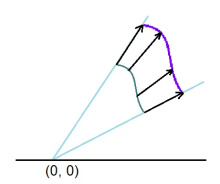
Ӧні ми висьталам Лобачевскӧй тшӧтшкӧсса куимпельӧсаяс йылысь.
Кыдзи ми тӧдам нин, веськыд визьясӧн лоӧны либӧ вертикальногса визьньӧвъяс (налӧн помыс куйлӧ абсцисса чӧрс вылын), либӧ кытшвизьджынъяс (налӧн шӧрыс куйлӧ абсцисса чӧрс вылын). Сідзкӧ, куимпельӧсалӧн доръясыс — либӧ вертикальногса вундӧгъяс, либӧ кытшвизьясыслӧн мегыръяс.
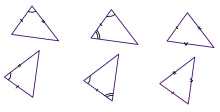
Ӧткодьлун тӧдмалан ногъяс. Школаын ми велӧдлім куимпельӧсаяслысь ӧткодьлунсӧ куим тӧдмалан ног:
1) кык дор да на костса пельӧс серти,
2) ӧти дор да сы бердса кык пельӧс серти,
3) куим дор серти.
Тайӧ теоремаяссӧ подулалігӧн параллельяс йылысь аксиома оз ков. Евклид геометрияысь Лобачевскӧй геометрияын кольӧ став аксиомаыс, параллель йылысь кындзи. Сідзкӧ, и тайӧ куим тӧдмалан ногыс кольӧ.
Вӧлӧмкӧ, Лобачевскӧй геометрияын куимпельӧсаяс ӧткодьлунлӧн эм нӧшта ӧти тӧдмалан ног:
4) куим пельӧс серти.
Теорема. Кор ABC да A’B’C’ – куимпельӧсаяс, ∠A = ∠A’, ∠B = ∠B’, ∠C = ∠C’, сэки ∆ABC = ∆A’B’C’.
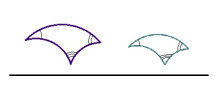
Евклид геометрияын татшӧм куимпельӧсаясыс сӧмын ӧтсямаӧсь, вермӧны лоны оз ӧткодьӧн.
Куимсэрӧглӧн эрд да пельӧсъяслӧн сумма. Сідзкӧ, Лобачевскӧй куимсэрӧгъяслысь ӧткодьлунсӧ позьӧ тӧдмавны сӧмын налӧн пельӧсъяс серти. Ӧткодь куимпельӧсаяслӧн эрдъясыс ӧткодьӧсь жӧ. Гашкӧ, позьӧ гижны кутшӧмкӧ формула куимсэрӧглӧн эрдлы, кытчӧ пырӧны сӧмын пельӧсъясыс? Вӧлӧмкӧ, позьӧ — и тайӧ формулаыс зэв кокньыд. Пондам кӧ муртавны пельӧсъяссӧ радианъясӧн, куимсэрӧглӧн эрдыс лоӧ
S = π − α − β − γ
(кӧні α, β, γ — куимсэрӧгыслӧн пельӧсъяс; π радиан лоӧ 180°).
Сідзкӧ, Лобачевскӧй куимсэрӧглӧн пельӧсъяслӧн суммаыс пыр лоӧ π радианысь (либӧ 180°-ысь) этшаджык. Евклид куимсэрӧглӧн тайӧ суммаыс пыр лоӧ 180° ыджда.
Пифагорлӧн теорема. Евклид геометрияысь ми тӧдам: веськыдпельӧса куимсэрӧглӧн кӧ катетъясыс a да b кузьтаӧсь, а гипотенузаыс c кузьта, сэки a² + b² = c².
Лобачевскӧй геометрияын эм Пифагор теоремалы аналог. Формулаыс со кутшӧм:
ch c = ch a ⋅ ch b,
кӧні a, b — катетъяс, c — гипотенуза, ch — гипербола косинус (сы йылысь ми коркӧ висьтавлім чеп визь йылысь гижӧдын).