Штейнерлӧн да Лемуслӧн теорема — различия между версиями
Наста (сёрнитанін | чӧжӧс) (→Содтӧд юӧр) |
Наста (сёрнитанін | чӧжӧс) (→Содтӧд юӧр) |
||
| Строка 26: | Строка 26: | ||
==Содтӧд юӧр== | ==Содтӧд юӧр== | ||
[https://lovziem.blogspot.com/2022/06/1.html Велӧдӧм паськӧдан блогын − 1.] | [https://lovziem.blogspot.com/2022/06/1.html Велӧдӧм паськӧдан блогын − 1.] | ||
| + | |||
[https://lovziem.blogspot.com/2022/07/2.html Велӧдӧм паськӧдан блогын − 2.] | [https://lovziem.blogspot.com/2022/07/2.html Велӧдӧм паськӧдан блогын − 2.] | ||
[[Category:Математика]] | [[Category:Математика]] | ||
Версия 19:11, 8 йирым 2022
Терминъяс
ӧткодь берда куимпельӧса — равнобедренный треугольник боквыв дор — боковая сторона судта — высота ӧткодь куимпельӧсаяс — равные треугольники
Штейнерлӧн да Лемуслӧн теорема
Школа геометрияысь ми тӧдам: куимпельӧса кӧ ӧткодь берда, сэки
- сылӧн боквыв доръяслань нуӧдӧм судтаяс ӧткузяӧсь,
- сылӧн боквыв доръяслань нуӧдӧм медианаяс ӧткузяӧсь,
- сылӧн боквыв доръяслань нуӧдӧм биссектрисаяс ӧткузяӧсь.
Позьӧ-ӧ шуны мӧдарӧ: куимпельӧсалӧн кӧ эм ӧткузя кык судта (медиана, биссектриса), сэки куимпельӧсаыс ӧткодь берда? Вӧлӧмкӧ, позьӧ.
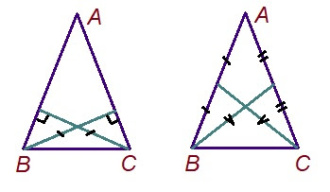
Судтаяс да медианаяс йылысь теоремаяссӧ абу вывті сьӧкыд подулавны; коді школа геометрия тӧдӧ, ӧдйӧ аддзас серпас вылысь ӧткодь куимпельӧсаяс да гӧгӧрвоас, мый ∠B = ∠C.
Вӧлӧмкӧ, биссектрисаяс йылысь теоремасӧ подулавны сьӧкыдджык нин. Медводзысь тайӧ теоремаыс вӧлі пасйӧма сӧмын 1840-ӧд воын, Шарль Штурм дорӧ Кристиан Лемуслӧн письмӧын. Сёрӧнджык сійӧс подулалӧма Якоб Штейнер; текстыс вель сьӧкыд, дай сэні тырмытӧмторъяс эмӧсь.
Сэсся унакодь подулалӧм вӧлі лӧсьӧдӧма; на пӧвстын эмӧсь дженьыдкодьяс, но быдын эм кутшӧмкӧ аслыспӧлӧс идея. Некымын йывсьыс ми мӧдысь гижам.