Штейнерлӧн да Лемуслӧн теорема — различия между версиями
Наста (сёрнитанін | чӧжӧс) (→Медводдза подулалӧм) |
Наста (сёрнитанін | чӧжӧс) (→Медводдза подулалӧм) |
||
| Строка 34: | Строка 34: | ||
Ӧні подулалам Штейнер−Лемуслысь теоремасӧ (босьтӧма татысь). Подулалӧмыс абу медся дженьыд, но меным сійӧ мичаӧн кажитчис. | Ӧні подулалам Штейнер−Лемуслысь теоремасӧ (босьтӧма татысь). Подулалӧмыс абу медся дженьыд, но меным сійӧ мичаӧн кажитчис. | ||
| − | ABC куимпельӧсалӧн BE да CF биссектрисаясыс ӧтыдждаӧсь. Колӧ петкӧдлыны: | + | ''ABC'' куимпельӧсалӧн ''BE'' да ''CF'' биссектрисаясыс ӧтыдждаӧсь. Колӧ петкӧдлыны: ∠''ABC'' = ∠''ACB''. |
| − | Гижтам GBE куимпельӧса сідзи, медым | + | Гижтам ''GBE'' куимпельӧса сідзи, медым ∆''GBE'' да ∆''AFC'' вӧліны ӧткодьӧсь, а ''G'' да ''A'' чутъяс куйлісны ӧти тшӧтшкӧсджынйын ''BE'' визь серти. |
| − | Миян артмӧ: | + | Миян артмӧ: ∠''BGE'' = ∠''BAE''. Сідзкӧ (планиметрия курсысь теорема серти) ''B'', ''G'', ''A'' да ''E'' чутъяс куйлӧны ӧти кытшвизь вылын. |
| − | Сідзкӧ | + | Сідзкӧ ∠''ABE'' = ∠''AGE'' (найӧ мыджсьӧны ӧти сійӧ жӧ мегырӧ да). |
| − | Гижтам GH — | + | Гижтам ''GH'' — ∆''BGE''-лысь биссектрисасӧ. Пасъям ''I'' шыпасӧн ''BE'' да ''CF''-лысь вомӧнасянінсӧ. |
| − | Петкӧдлам: | + | Петкӧдлам: ∠''AIE'' = ∠''AGH''. |
| − | + | ∠''AIE'' лоӧ ∆''BAI''-лӧн ортсы пельӧсӧн; формула серти, | |
| − | + | ∠''AIE'' = ∠''ABI'' + ∠''BAI''. | |
| − | I чут — ABC куимпельӧсалӧн биссектрисаяслӧн вомӧнасянін, та вӧсна | + | ''I'' чут — ''ABC'' куимпельӧсалӧн биссектрисаяслӧн вомӧнасянін, та вӧсна |
| − | + | ∠''BAI'' = ∠''BAC''/2. | |
| − | Но | + | Но ∆''GBE'' = ∆''AFC'', та вӧсна ∠''BAC''/2 = ∠''BGE''/2 = ∠''EGH''. |
Сідзкӧ | Сідзкӧ | ||
| − | + | ∠''BAI'' = ∠''EGH''. | |
| − | + | Кыдзи ми тӧдам нин, ∠''ABE'' = ∠''AGE'', а ∠''ABI'' да ∠''ABE'' — ӧти сійӧ жӧ пельӧс. Сідзкӧ | |
| − | + | ∠''ABI'' = ∠''AGE''. | |
Миян артмис: | Миян артмис: | ||
| − | + | ∠''AIE'' = ∠''ABI'' + ∠''BAI'' = ∠''AGE'' + ∠''EGH'' = ∠''AGH''. | |
| + | Ӧні казялам: ∠''AIE'' + ∠''AIH'' = 180°; сідзкӧ | ||
| − | + | ∠''AGH'' + ∠''AIH'' = 180°. | |
| − | + | Та вӧсна ''A'', ''G'', ''H'', ''I'' чутъяс куйлӧны ӧти кытшвизь вылын (планиметрия курсысь теорема серти). | |
| − | Та вӧсна | + | Казьтыштам: ''GH'' да ''AI'' — ӧткодь куимсэрӧгъяслӧн лӧсялана пельӧсъяслӧн биссектрисаяс; сідзкӧ найӧ ӧтыдждаӧсь. Миян артмӧ: ''GH'' да ''AI'' — ӧтыджда хордаяс. Та вӧсна ''IH'' да ''AG'' вундӧгъяс — параллельяс. |
| − | + | Ӧні ми вермам петкӧдлыны, мый ∠''ABC'' = ∠''ACB''. | |
| − | |||
| − | Ӧні ми вермам петкӧдлыны, мый | ||
Ми тӧдам нин: | Ми тӧдам нин: | ||
| − | + | ∠''ABC''/2 = ∠''ABE'' = ∠''AGE''; | |
| − | + | ∠''ACB''/2 = ∠''ACF'' = ∠''GEB'' (лӧсялана пельӧсъяс ӧткодь куимсэрӧгъясын); | |
| − | + | ∠''AGE'' = ∠''GEB'' (ӧтар-мӧдар куйлысь пельӧсъяс; ''AG'' да ''BE'' — параллельяс). | |
| − | Сідзкӧ | + | Сідзкӧ ∠''ABC''/2 = ∠''ACB''/2, кытысь ∠''ABC'' = ∠''ACB''. |
==Мӧд подулалӧм== | ==Мӧд подулалӧм== | ||
Версия 19:22, 8 йирым 2022
Содержание
Терминъяс
куимпельӧса, куимсэрӧг — треугольник ӧткодь берда куимпельӧса — равнобедренный треугольник боквыв дор — боковая сторона судта — высота ӧткодь куимпельӧсаяс — равные треугольники ӧткодь куимсэрӧгъяс — равные треугольники лӧсялана пельӧсъяс — соответствующие углы (в равных треугольниках) тшӧтшкӧсджын — полуплоскость ортсы пельӧс — внешний угол ӧтар-мӧдар куйлысь пельӧсъяс — накрест лежащие углы
Штейнерлӧн да Лемуслӧн теорема
Школа геометрияысь ми тӧдам: куимпельӧса кӧ ӧткодь берда, сэки
- сылӧн боквыв доръяслань нуӧдӧм судтаяс ӧткузяӧсь,
- сылӧн боквыв доръяслань нуӧдӧм медианаяс ӧткузяӧсь,
- сылӧн боквыв доръяслань нуӧдӧм биссектрисаяс ӧткузяӧсь.
Позьӧ-ӧ шуны мӧдарӧ: куимпельӧсалӧн кӧ эм ӧткузя кык судта (медиана, биссектриса), сэки куимпельӧсаыс ӧткодь берда? Вӧлӧмкӧ, позьӧ.
Судтаяс да медианаяс йылысь теоремаяссӧ абу вывті сьӧкыд подулавны; коді школа геометрия тӧдӧ, ӧдйӧ аддзас серпас вылысь ӧткодь куимпельӧсаяс да гӧгӧрвоас, мый ∠B = ∠C.
Вӧлӧмкӧ, биссектрисаяс йылысь теоремасӧ подулавны сьӧкыдджык нин. Медводзысь тайӧ теоремаыс вӧлі пасйӧма сӧмын 1840-ӧд воын, Шарль Штурм дорӧ Кристиан Лемуслӧн письмӧын. Сёрӧнджык сійӧс подулалӧма Якоб Штейнер; текстыс вель сьӧкыд, дай сэні тырмытӧмторъяс эмӧсь.
Сэсся унакодь подулалӧм вӧлі лӧсьӧдӧма; на пӧвстын эмӧсь дженьыдкодьяс, но быдын эм кутшӧмкӧ аслыспӧлӧс идея. Некымын йывсьыс ми мӧдысь гижам.
Медводдза подулалӧм
Ӧні подулалам Штейнер−Лемуслысь теоремасӧ (босьтӧма татысь). Подулалӧмыс абу медся дженьыд, но меным сійӧ мичаӧн кажитчис.
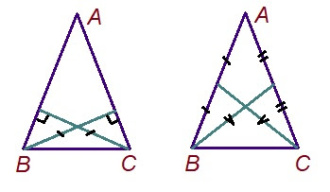
ABC куимпельӧсалӧн BE да CF биссектрисаясыс ӧтыдждаӧсь. Колӧ петкӧдлыны: ∠ABC = ∠ACB.
Гижтам GBE куимпельӧса сідзи, медым ∆GBE да ∆AFC вӧліны ӧткодьӧсь, а G да A чутъяс куйлісны ӧти тшӧтшкӧсджынйын BE визь серти.
Миян артмӧ: ∠BGE = ∠BAE. Сідзкӧ (планиметрия курсысь теорема серти) B, G, A да E чутъяс куйлӧны ӧти кытшвизь вылын.
Сідзкӧ ∠ABE = ∠AGE (найӧ мыджсьӧны ӧти сійӧ жӧ мегырӧ да).
Гижтам GH — ∆BGE-лысь биссектрисасӧ. Пасъям I шыпасӧн BE да CF-лысь вомӧнасянінсӧ.
Петкӧдлам: ∠AIE = ∠AGH.
∠AIE лоӧ ∆BAI-лӧн ортсы пельӧсӧн; формула серти,
∠AIE = ∠ABI + ∠BAI.
I чут — ABC куимпельӧсалӧн биссектрисаяслӧн вомӧнасянін, та вӧсна
∠BAI = ∠BAC/2.
Но ∆GBE = ∆AFC, та вӧсна ∠BAC/2 = ∠BGE/2 = ∠EGH.
Сідзкӧ
∠BAI = ∠EGH.
Кыдзи ми тӧдам нин, ∠ABE = ∠AGE, а ∠ABI да ∠ABE — ӧти сійӧ жӧ пельӧс. Сідзкӧ
∠ABI = ∠AGE.
Миян артмис:
∠AIE = ∠ABI + ∠BAI = ∠AGE + ∠EGH = ∠AGH.
Ӧні казялам: ∠AIE + ∠AIH = 180°; сідзкӧ
∠AGH + ∠AIH = 180°.
Та вӧсна A, G, H, I чутъяс куйлӧны ӧти кытшвизь вылын (планиметрия курсысь теорема серти).
Казьтыштам: GH да AI — ӧткодь куимсэрӧгъяслӧн лӧсялана пельӧсъяслӧн биссектрисаяс; сідзкӧ найӧ ӧтыдждаӧсь. Миян артмӧ: GH да AI — ӧтыджда хордаяс. Та вӧсна IH да AG вундӧгъяс — параллельяс.
Ӧні ми вермам петкӧдлыны, мый ∠ABC = ∠ACB.
Ми тӧдам нин:
∠ABC/2 = ∠ABE = ∠AGE;
∠ACB/2 = ∠ACF = ∠GEB (лӧсялана пельӧсъяс ӧткодь куимсэрӧгъясын);
∠AGE = ∠GEB (ӧтар-мӧдар куйлысь пельӧсъяс; AG да BE — параллельяс).
Сідзкӧ ∠ABC/2 = ∠ACB/2, кытысь ∠ABC = ∠ACB.